Light


Новичок
|
      
Здравствуйте, будьте так добры, помогите пожалуйста доказать сходимость или расходимость ряда (использовав два разных признака):

Заранее премного благодарна!
|
Всего сообщений: 23 | Присоединился: декабрь 2008 | Отправлено: 26 окт. 2009 0:44 | IP
|
|
Fenja544


Новичок
|
      
1. Исследовать сходимость числового ряда:
беск.
СУММ n3 / (2n)!
n=1
2. Найти область сходимости степенного ряда:
беск.
СУММ ((x-2)^n)/ n*(n+1)
n=1
3. Вычислить определенный интеграл с точностью до 0,001. Для этого подынтегральную функцию разложить в степенной ряд, который затем почленно проинтегрировать:
0,5
int x*ln(1+x^2)dx
0
|
Всего сообщений: 40 | Присоединился: октябрь 2009 | Отправлено: 2 нояб. 2009 19:17 | IP
|
|
Rabbit


Новичок
|
     
Помогите, пожалуйста, исследовать на сходимоть ряд, а то что то у меня не выходит. 
|
Всего сообщений: 4 | Присоединился: ноябрь 2009 | Отправлено: 3 нояб. 2009 14:33 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Rabbit написал 3 нояб. 2009 14:33
Помогите, пожалуйста, исследовать на сходимоть ряд, а то что то у меня не выходит. 
^{n} }{2^{n}(2n-1)} )
Найдем радиус R сходимости данного степенного ряда.
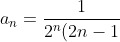} )
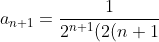 - 1)} = \frac{1}{2^{n+1}(2n+1)} )
}{2^{n}(2n-1)} = \lim\limits_{n \to \infty} \frac{4n+2}{2n-1} = )
}{n(2-\frac{1}{n})} = \lim\limits_{n \to \infty} \frac{4+\frac{2}{n} }{2-\frac{1}{n} } = \frac{4+0}{2-0} = 2 )
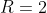
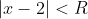
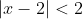
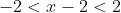
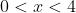
Таким образом, исходный степенной ряд ^{n} }{2^{n}(2n-1)} ) сходится на интервале сходится на интервале  ) . .
Рассмотрим граничные точки x = 0 и x = 4.
При x = 4 исходный степенной ряд ^{n} }{2^{n}(2n-1)} ) принимает вид принимает вид 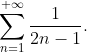
Это гармонический ряд, который является расходящимся.
Таким образом, в точке x = 4 исходный степенной ряд ^{n} }{2^{n}(2n-1)} ) расходится. расходится.
При x = 0 исходный степенной ряд ^{n} }{2^{n}(2n-1)} ) принимает вид принимает вид ^{n} }{2n-1}. )

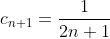

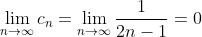
По теореме Лейбница ряд ^{n} }{2n-1} ) сходится. сходится.
Следовательно, в точке x=0 исходный степенной ряд ^{n} }{2^{n}(2n-1)} ) сходится. сходится.
Таким образом, исходный степенной ряд ^{n} }{2^{n}(2n-1)} ) сходится на интервале сходится на интервале . )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 3 нояб. 2009 22:16 | IP
|
|
Rabbit


Новичок
|
     
Огромно спасибо, была б возможность поцеловала б 
|
Всего сообщений: 4 | Присоединился: ноябрь 2009 | Отправлено: 4 нояб. 2009 11:20 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Fenja544 написал 2 нояб. 2009 19:17
2. Найти область сходимости степенного ряда:
беск.
СУММ ((x-2)^n)/ n*(n+1)
n=1
^{n} }{n(n+1)} )
Найдем радиус R сходимости данного степенного ряда.
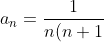} )
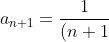(n+2)} )
(n+2)}{n(n+1)}| = )
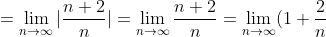 = 1 + 0 = 1 )
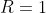
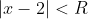
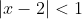
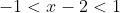
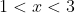
Таким образом, исходный степенной ряд ^{n} }{n(n+1)} ) сходится на интервале сходится на интервале . )
Рассмотрим граничные точки x = 1 и x = 3.
При x = 3 исходный степенной ряд ^{n} }{n(n+1)} ) принимает вид принимает вид 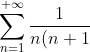}. )
Данный ряд является сходящимся.
Следовательно, в точке x = 3 исходный степенной ряд ^{n} }{n(n+1)} ) сходится. сходится.
При x = 1 исходный степенной ряд ^{n} }{n(n+1)} ) принимает вид принимает вид ^{n} }{n(n+1)}. )
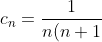} )
 < (n+1)(n+2) \ \ \Rightarrow \ \ \frac{1}{n(n+1)} > \frac{1}{(n+1)(n+2)} \ \ \Rightarrow \ \ c_{n} > c_{n+1} )
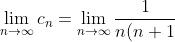} = 0 )
По теореме Лейбница ряд ^{n} }{n(n+1)} ) сходится. сходится.
Следовательно, исходный степенной ряд ^{n} }{n(n+1)} ) сходится в точке x = 1. сходится в точке x = 1.
Значит, исходный степенной ряд ^{n} }{n(n+1)} ) сходится на отрезке сходится на отрезке 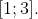
(Сообщение отредактировал RKI 5 нояб. 2009 11:28)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 5 нояб. 2009 11:27 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Fenja544 написал 2 нояб. 2009 19:17
3. Вычислить определенный интеграл с точностью до 0,001. Для этого подынтегральную функцию разложить в степенной ряд, который затем почленно проинтегрировать:
0,5
int x*ln(1+x^2)dx
0
 = \sum_{n=1}^{+\infty} \frac{(-1)^{n+1}x^{n} }{n} )
 = \sum_{n=1}^{+\infty} \frac{(-1)^{n+1}x^{2n} }{n} )
 = \sum_{n=1}^{+\infty} \frac{(-1)^{n+1}x^{2n+1} }{n} )
 dx = \int\sum_{n=1}^{+\infty} \frac{(-1)^{n+1}x^{2n+1} }{n} dx = )
^{n+1}x^{2n+1} }{n} dx = \sum_{n=1}^{+\infty} \frac{(-1)^{n+1} }{n} \int x^{2n+1} dx = )
^{n+1}x^{2n+2} }{n(2n+2)} )
 = \sum_{n=1}^{+\infty} \frac{(-1)^{n+1}x^{2n+2} }{n(2n+2)} )
 = 0 )
 = \sum\limits_{n=1}^{+\infty} \frac{(-1)^{n+1}(0.5)^{2n+2} }{n(2n+2)} = \sum\limits_{n=1}^{+\infty} \frac{(-1)^{n+1}(0.25)^{n+1} }{2n(n+1)} = \sum\limits_{n=1}^{+\infty} \frac{(-0.25)^{n+1} }{2n(n+1)} )
dx = F(0.5) - F(0) = \sum\limits_{n=1}^{+\infty} \frac{(-0.25)^{n+1} }{2n(n+1)} )
Возьмем сначала один член ряда.
dx \sim 0.015625 )
Возьмем два члена ряда.
dx \sim 0.015625 - 0.001302 = 0.014323 )
Возьмем три члена ряда.
dx \sim 0.015625 - 0.001302 + 0.000163 = 0.014486 )
Возьмем четыре члена ряда.
dx \sim 0.015625 - 0.001302 + 0.000163 - 0.000024 = 0.014462 )
Нас интересует точность 0,001, то есть до третьего знака после запятой.
Далее будут всё меньшие и меньшие члены ряда. Следовательно,
dx \sim 0.014 )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 5 нояб. 2009 13:13 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Fenja544 написал 2 нояб. 2009 19:17
1. Исследовать сходимость числового ряда:
беск.
СУММ n3 / (2n)!
n=1
В числителе 3n или n^3 или что-то еще?
Огромная просьба. Удалите все дублирующие сообщения с задачами, так как одну и ту же задачу могут решать два отвечающих в разных темах. Заранее спасибо.
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 5 нояб. 2009 13:16 | IP
|
|
Fenja544


Новичок
|
      
n^3
Помогите решить!это последнее!
Исследовать сходимость числового ряда:
беск.
СУММ n^3 / (2n)!
n=1
(Сообщение отредактировал attention 26 фев. 2010 23:37)
|
Всего сообщений: 40 | Присоединился: октябрь 2009 | Отправлено: 5 нояб. 2009 13:44 | IP
|
|
attention 


Долгожитель
|
      
Цитата: Fenja544 написал 7 нояб. 2009 14:01
Помогите решить!это последнее!
Исследовать сходимость числового ряда:
беск.
СУММ n^3 / (2n)!
n=1
Воспользуйтесь признаком Даламбера:


Следовательно, согласно признаку Даламбера исходный ряд сходится.
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 7 нояб. 2009 19:53 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.1.17 Вопросы сходимости рядов
2.1.17 Вопросы сходимости рядов

 Форум
Форум

 Математика
Математика

 2.1.17 Вопросы сходимости рядов
2.1.17 Вопросы сходимости рядов