aly17

Участник
|
     
там правильно всё,кроме того что заместо 13 там -13
за 2-ой спасиб)))
|
Всего сообщений: 107 | Присоединился: декабрь 2008 | Отправлено: 20 мая 2009 22:11 | IP
|
|
marika91

Новичок
|
      
помогите пжл!надо привести ур-е кривой 2-ого порядка к каноническому виду методом собственных значений
9*x^2 + 6*x*y + y^2 - 17*sqrt10*x - 9*sqrt10*y + 80 = 0
|
Всего сообщений: 8 | Присоединился: май 2009 | Отправлено: 21 мая 2009 17:24 | IP
|
|
Magistr

Новичок
|
      
Здравствуйте. Помогите пожалуйста решить:
1)Составить уравнение прямой, проходящей через точку А(1,2) так, что отрезок этой прямой, заключенный между прямыми 3x+y+2=0 и 4x+y=1, в точке А делится пополам.
2)Точки (1,2), (-3,0) - вершины равнобедренного треугольника АВС, угол А = угол В = arccos(1/sqrt(5)). Насти координаты С, зная, что она лежит по ту сторону от прямой АВ, что и точка М(2,3).
3)Рассматривается тот угол между прямыми y=x+1 и y=7x+1, внутри которого лежит точка А(1,3). Найти координаты точки В, лежащей внутри этого угла и удаленной от данных прямых соответственно на расстояния 4sqrt(2) и sqrt(2).
4)Точка Н(-3,2) является точкой пересечения высот треугольника, две стороны которого лежат на прямых y=2x и y=-x+3. Составить уравнение третьей стороны.
5)Составить уравнения прямых, параллельных прямой -2x+y+5=0 и отстоящих от точки (1,-2) на расстояние sqrt(20).
6)Написать уравнение прямой, которая симметрична прямой (заданной параметрически) x=1+t y=2-2t z=-1-t ; относительно другой прямой (заданной параметрически)x=-1-2t y=t z=2+3t.
Заранее благодарен. Был бы очень признателен за наличие рисунков.
(Сообщение отредактировал Magistr 31 мая 2009 13:42)
|
Всего сообщений: 9 | Присоединился: май 2009 | Отправлено: 31 мая 2009 13:21 | IP
|
|
Kristisha

Новичок
|
        
Помогите, пожалуйста, очень срочно необходимо!!!!!
Найти площадь треугольника, вершины которого – точки А(3; П/8), В(8; 7П/24) и С(6; 5П/8)
|
Всего сообщений: 3 | Присоединился: сентябрь 2009 | Отправлено: 18 сен. 2009 11:53 | IP
|
|
|
|
venom11


Новичок
|
      
Помогите,пожалуйста,с таким заданием (кто что может решить-решите,будьте друзьями ): ):
Даны вершини треугольника А(-1;-1),В(5;2),С(2;5).Найти:
1)длину стороны АВ ;
2)тангенс внутреннего угла А ;
3)уравнение высоты,проведённой через вершину С ;
4)уравнение медианы,проведённой через вершину С ;
5)точку пересечения высот треугольника ;
6)длину высоты,опущенной из вершины С ;
7)площадь треугольника АВС ;
8)систему линейных неравенств,котрые определяют треугольник АВС.
|
Всего сообщений: 7 | Присоединился: сентябрь 2009 | Отправлено: 24 сен. 2009 19:32 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: venom11 написал 24 сен. 2009 19:32
Даны вершини треугольника А(-1;-1),В(5;2),С(2;5).Найти:
1)длину стороны АВ ;
 )
 )
 )
^2 + (2+1)^2} = \sqrt{36+9} = \sqrt{45} = 3\sqrt{5} )
Цитата: venom11 написал 24 сен. 2009 19:32
3)уравнение высоты,проведённой через вершину С ;
 )
 )
 )
Напишем уравнение стороны AB. Уравнение стороны AB имеет вид:
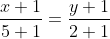
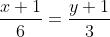
 )
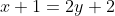
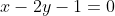
Обозначим CH - высота, проведенная из вершины C. Другими словами, CH - перпендикуляр к стороне AB, проходящий через точку C.
Пусть уравнение прямой CH имеет вид 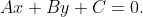
Коэффициенты A, B и C необходимо найти.
Прямые CH и AB перпендикулярны. По условию перпендикулярности двух прямых  = 0 )
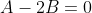
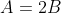
Следовательно, уравнение высоты CH примет вид:
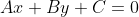
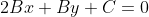
Прямая CH проходит через точку C. Следовательно, координаты точки C удовлетворяют уравнению прямой CH:
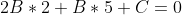
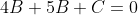
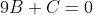
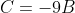
Следовательно, уравнение высоты CH примет вид:
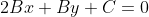
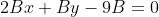
Делим на B, отличное от нуля. И в результате получаем уравнение высоты, опущенной из вершины C:
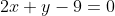
Цитата: venom11 написал 24 сен. 2009 19:32
6)длину высоты,опущенной из вершины С ;
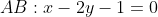
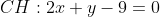
Необходимо найти длину отрезка CH. Найдем координаты точки H. Точка H является точкой пересечения двух прямых AB и CH. Следовательно, для нахождения координат точки H необходимо решить систему линейных уравнений:
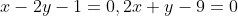
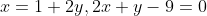
 + y - 9 = 0 )
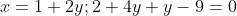
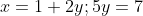
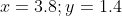
 )
 )
^2 + (1.4 - 5)^2} = \sqrt{3.24 + 12.96} = \sqrt{16.2} )
Цитата: venom11 написал 24 сен. 2009 19:32
7)площадь треугольника АВС ;
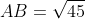
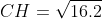
 = \frac{1}{2} * AB * CH = \frac{1}{2} * \sqrt{45} * \sqrt{16.2} = \frac{1}{2} * \sqrt{729} = \frac{1}{2} * 27 = 13.5 )
Цитата: venom11 написал 24 сен. 2009 19:32
2)тангенс внутреннего угла А ;
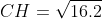
 )
 )
^2 + (1.4+1)^2} = \sqrt{23.04 + 5.76} = \sqrt{28.8} )
Рассмотрим треугольник ACH. Он является прямоугольным (угол AHC равен 90 градусов). По определению тангенса угла в прямоугольном треугольнике
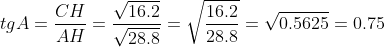
Цитата: venom11 написал 24 сен. 2009 19:32
5)точку пересечения высот треугольника ;
 )
 )
 )
Напишем уравнение стороны AC. Уравнение стороны AC имеет вид:
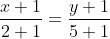
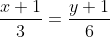
 = y + 1 )
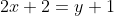
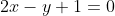
Обозначим BK - высота, проведенная из вершины B. Другими словами, BK - перпендикуляр к стороне AC, проходящий через точку B.
Пусть уравнение прямой BK имеет вид 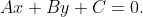
Коэффициенты A, B и C необходимо найти.
Прямые BK и AC перпендикулярны. По условию перпендикулярности двух прямых  = 0 )
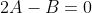
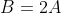
Следовательно, уравнение высоты BK примет вид:
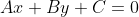
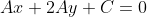
Прямая BK проходит через точку B. Следовательно, координаты точки B удовлетворяют уравнению прямой BK:
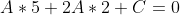
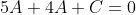
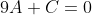
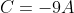
Следовательно, уравнение высоты BK примет вид:
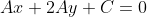
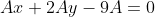
Делим на A, отличное от нуля. И в результате получаем уравнение высоты, опущенной из вершины B:
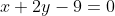
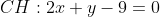
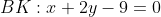
Пусть точка O - точка пересечения высот треугольника, то есть точка пересечения прямых CH и BK. Для нахождения координат точки O необходимо решить систему линейных уравнений:
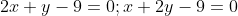
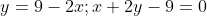
 - 9 = 0 )

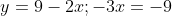
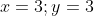
 )
Цитата: venom11 написал 24 сен. 2009 19:32
4)уравнение медианы,проведённой через вершину С ;
Обозначим CM - медиана, проведенная через вершину C. По определению медианы треугольника точка M является серединой отрезка AB. Следовательно,
 )
 )
 )
 )
Тогда уравнение прямой CM имеет вид:
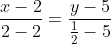
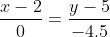
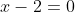
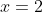
Цитата: venom11 написал 24 сен. 2009 19:32
8)систему линейных неравенств,котрые определяют треугольник АВС.
Уравнение стороны AB имеет вид 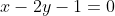
Подставим в левую часть этого уравнения координаты точки C.
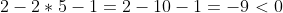
Следовательно, первое неравенство системы имеет вид:
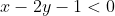
Уравнение стороны AC имеет вид: 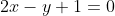
Подставим в левую часть этого уравнения координаты точки B.
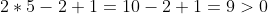
Следовательно, второе неравество системы имеет вид:
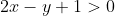
Уравнение стороны BC имеет вид:
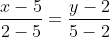
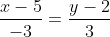
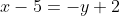
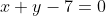
Подставим в левую часть этого уравнения координаты точки A.
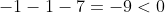
Следовательно, третье неравенство системы имеет вид:
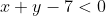
Таким образом, система линейных неравенств, определяющих треугольник ABC, имеет вид:
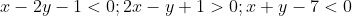
(Сообщение отредактировал attention 10 дек. 2009 14:46)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 25 сен. 2009 10:27 | IP
|
|
kibdaria

Новичок
|
     
Помогите пожалуйста с решением!!!!!!!!!!!!!даны вершина А (7;4) В (-9;-8) С (-2;16) треугольника АВС найти : 1 длинну и уравнение стороны ВС 2 площадь треугольника 3 длину и уравнение высоты проведённой из вершины А 4 уравнение биссектрисы внутреннего угла В 5 сделать чертёж
|
Всего сообщений: 4 | Присоединился: сентябрь 2009 | Отправлено: 26 сен. 2009 9:24 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: kibdaria написал 26 сен. 2009 9:24
Помогите пожалуйста с решением!!!!!!!!!!!!!даны вершина А (7;4) В (-9;-8) С (-2;16) треугольника АВС найти : 1 длинну и уравнение стороны ВС
 )
 )
^2 + (11+8)^2} = \sqrt{49+361} = \sqrt{380} = 2\sqrt{95} )
Уравнение стороны BC имеет вид:
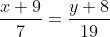
 = 7(y+8) )
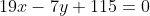
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 26 сен. 2009 11:05 | IP
|
|
venom11


Новичок
|
      
RKI,огромнейшее спасибо!!!!
|
Всего сообщений: 7 | Присоединился: сентябрь 2009 | Отправлено: 26 сен. 2009 16:08 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 2.9.1 Аналитическая геометрия
2.9.1 Аналитическая геометрия

 Форум
Форум

 Математика
Математика

 2.9.1 Аналитическая геометрия
2.9.1 Аналитическая геометрия