ProstoVasya

Долгожитель
|
     
Yoh
Не понятно условие. Например, какая первая дробь?
Такая х-5/ 4, или всё же такая (х-5)/ 4
Cardiff
1. Точка А лежит на оси ординат. Следовательно, на плоскости Оxz.
Точка B (1;0;1) тоже лежит на плоскости Оxz. Следовательно, прямая, проходящая через эти точки лежит на плоскости Оxz. Угол между плоскостью и прямой равен 0.
2. a = t*b = t*(6;8;-7,5). Т.к. а образует тупой угол с координатным вектором j, то t < 0.
Далее, |a|^2 = 2500. Поэтому
(6^2 + 8^2 + 7.5^2)*t^2 = 2500
Отсюда, t = -4.
Ответ: a=(-24, -32, 30)
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 27 окт. 2009 17:58 | IP
|
|
Cardiff


Новичок
|
     
ProstoVasya ,
спасибо за вторую задачу,но в первой нужно найти не угол,а координаты точки А
|
Всего сообщений: 17 | Присоединился: октябрь 2009 | Отправлено: 27 окт. 2009 18:08 | IP
|
|
ProstoVasya

Долгожитель
|
     
Cardiff
Правильно, нужно найти не угол,а координаты точки А. Но, как?
В условии сказано, что AB состовляет с плоскостью Оxz угол в 30 градусов. Чего быть не может, т.к. она лежит на плоскости Оxz .
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 27 окт. 2009 18:15 | IP
|
|
Cardiff


Новичок
|
     
но ведь А лежит на ординате,значит только y у нее равен нулю
|
Всего сообщений: 17 | Присоединился: октябрь 2009 | Отправлено: 27 окт. 2009 19:59 | IP
|
|
ProstoVasya

Долгожитель
|
     
Cardiff
Обратите внимание на координаты точки В(1,0,1). Она тоже лежит на плоскости Оxz . Возможно, в координатах этой точки ошибка?
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 27 окт. 2009 20:20 | IP
|
|
Cardiff


Новичок
|
     
нет.Но и точка А лежит не в Оxz,а на Оy,и только эта координата равна нулю
|
Всего сообщений: 17 | Присоединился: октябрь 2009 | Отправлено: 27 окт. 2009 20:22 | IP
|
|
ProstoVasya

Долгожитель
|
     
Извините, я перепутал ось ординат с осью абсцисс.
Тогда так.
Рассмотрим вектор BA. У него координаты {-1,y,-1}
Угол t между этим вектором и осью OY (вектором j) равен либо 60 градусов, либо 120 градусов. Рассмотрим скалярное произведение AB*j = y
или
|AB| cos(t) = y
Возведём в квадрат, получим
(1 + y^2 +1) = 4 y^2
Отсюда, y^2 = 2/3
Ответ: y = sqrt(2/3) или y = - sqrt(2/3)
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 27 окт. 2009 20:45 | IP
|
|
W1zzarD


Новичок
|
      
А1(6,6,5) А2(4,9,5) А3(4,6,11) А4(6,9,3)
По координатам вершин пирамиды А1А2А3А4 найти:
1. Угол между ребром А1А4 и гранью А1А2А3
2. Площадь грани А1А2А3
3. Обьём пирамиды
4. Уравнение прямой А1А2
5. Уравнение плоскости А1А2А3
6. Уравнение высоты, опущенной из вершины А4 на грань А1А2А3
|
Всего сообщений: 1 | Присоединился: октябрь 2009 | Отправлено: 28 окт. 2009 19:41 | IP
|
|
Cardiff


Новичок
|
     
Помогите пожалуйста решить!!
в прямом параллелепипеде боковое ребро равно 10. Большая диагональ основания равна 9 и образует с большей стороной основания, равной 7, угол, синус которого (4*sqrt(5))\21. Определить боковую поверхность параллелепипеда.
|
Всего сообщений: 17 | Присоединился: октябрь 2009 | Отправлено: 29 окт. 2009 15:50 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: W1zzarD написал 28 окт. 2009 19:41
А1(6,6,5) А2(4,9,5) А3(4,6,11) А4(6,9,3)
4. Уравнение прямой А1А2
 )
 )
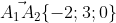
Уравнение прямой A1A2 имеет вид:
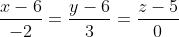
Цитата: W1zzarD написал 28 окт. 2009 19:41
А1(6,6,5) А2(4,9,5) А3(4,6,11) А4(6,9,3)
5. Уравнение плоскости А1А2А3
 )
 )
 )
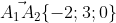
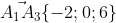
Уравнение плоскости A1A2A3 имеет вид:
|x-6 y-6 z-5| = 0
| -2 3 0|
| -2 0 6|
(x-6)*|3 0| - (y-6)*|-2 0| + (z-5)*|-2 3| = 0
|0 6| |-2 6| |-2 0|
(x-6)*(18 - 0) - (y-6)*(-12-0) + (z-5)*(0+6) = 0
18(x-6) + 12(y-6) + 6(z-5) = 0
3(x-6) + 2(y-6) + z - 5 = 0
3x - 18 + 2y - 12 + z - 5 = 0
3x + 2y + z - 35 = 0
Цитата: W1zzarD написал 28 окт. 2009 19:41
А1(6,6,5) А2(4,9,5) А3(4,6,11) А4(6,9,3)
6. Уравнение высоты, опущенной из вершины А4 на грань А1А2А3
Пусть A4H - высота, опущенная на грань A1A2A3 (точка H лежит на грани A1A2A3).
 )
Уравнение высоты A4H имеет вид:
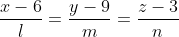
Коэффициенты l, m и n необходимо найти.
Прямая A4H и плоскость A1A2A3: 3x + 2y + z - 35 = 0 перпендикулярны. По условию перпендикулярности прямой и плоскости в пространстве:
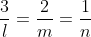
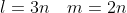
Уравнение высоты A4H имеет вид:
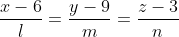
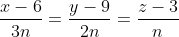
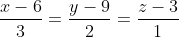
Цитата: W1zzarD написал 28 окт. 2009 19:41
А1(6,6,5) А2(4,9,5) А3(4,6,11) А4(6,9,3)
2. Площадь грани А1А2А3
 )
 )
 )
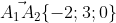
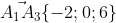
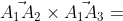
| i j k|
= |-2 3 0| = i*|3 0| - j*|-2 0| + k*|-2 3| =
|-2 0 6| |0 6| |-2 6| |-2 0|
= i*(18 - 0) - j*(-12 - 0) + k*(0 + 6) = 18i + 12j + 6k
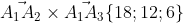
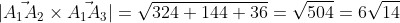
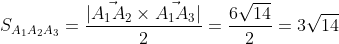
Цитата: W1zzarD написал 28 окт. 2009 19:41
А1(6,6,5) А2(4,9,5) А3(4,6,11) А4(6,9,3)
3. Обьём пирамиды
 )
 )
 )
 )
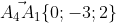
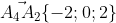
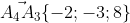
 = )
| 0 -3 2|
= |-2 0 2| = 0*| 0 2| - (-3)*|-2 2| + 2*|-2 0| =
|-2 -3 8| |-3 8| |-2 8| |-2 -3|
= 0 + 3*(-16+4) + 2*(6-0) = 0 - 36 + 12 = - 24
|}{6} = \frac{24}{6} = 4 )
Цитата: W1zzarD написал 28 окт. 2009 19:41
А1(6,6,5) А2(4,9,5) А3(4,6,11) А4(6,9,3)
1. Угол между ребром А1А4 и гранью А1А2А3
Уравнение грани A1A2A3: 3x + 2y + z - 35 = 0.
A = 3
B = 2
C = 1
 )
 )
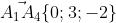
Уравнение прямой A1A4 имеет вид:
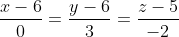
l = 0
m = 3
n = -2
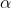 - угол между прямой A1A4 И гранью A1A2A3. - угол между прямой A1A4 И гранью A1A2A3.
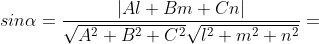
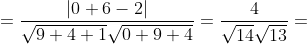
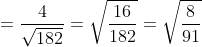
 )
Цитата: Cardiff написал 29 окт. 2009 15:50
Помогите пожалуйста решить!!
в прямом параллелепипеде боковое ребро равно 10. Большая диагональ основания равна 9 и образует с большей стороной основания, равной 7, угол, синус которого (4*sqrt(5))\21. Определить боковую поверхность параллелепипеда.
CC1 = 10
AC = 9
AD = 7
sinCAD = 4sqrt(5)/21
S(AA1D1D) = AA1*AD = 10*7 = 70
CD = AC*sinCAD = 9*4sqrt(5)/21 = 12sqrt(5)/7
S(DD1C1C) = CC1*CD = 120sqrt(5)/7
S(бок) = 2*(S(AA1D1D) + S(DD1C1C)) = 2(70 + 120sqrt(5)/7)
(Сообщение отредактировал attention 10 дек. 2009 15:21)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 30 окт. 2009 14:24 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 2.9.1 Аналитическая геометрия
2.9.1 Аналитическая геометрия

 Форум
Форум

 Математика
Математика

 2.9.1 Аналитическая геометрия
2.9.1 Аналитическая геометрия