SSSergey


Новичок
|
     
Цитата: RKI написал 26 окт. 2009 12:09
Цитата: SSSergey написал 25 окт. 2009 23:34
Помогите решите пожалуйста ещё матричное исчисление

решить любым способом или каким-то конкретным?
извиняюсь не правильно написал в матричном исчислении)))
|
Всего сообщений: 27 | Присоединился: октябрь 2009 | Отправлено: 26 окт. 2009 12:54 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: SSSergey написал 25 окт. 2009 23:34
3)расстояние от вершины C до медианы, проведенной из вершины B;
A(22; -6), B(-2; 1), C(-6; -2).
Пусть BM - медиана, где точка M лежит на стороне AC. Так как BM - медиана треугольника, то точка M является серединой стороны AC.
 )
 )
 )
 )
 )
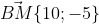
Уравнение медианы BM имеет вид:
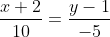
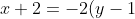 )
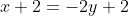
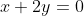
Проведем к медиане BM перпендикуляр CK, где точка K лежит на медиане BM.
Пусть уравнение прямой CK имеет вид ax + by + c = 0. Коэффициенты a, b и c необходимо определить.
Прямые BM: x + 2y = 0 и CK: ax + by + c = 0 перпендикулярны. По условию перпендикулярности двух прямых
a + 2b = 0
a = - 2b
Уравнение прямой CK принимает вид:
ax + by + c = 0
- 2bx + by + c = 0
Точка C (-6;-2) лежит на прямой CK. Значит, координаты точки C удовлетворяют уравнению прямой CK:
- 2b*(-6) + b*(-2) + c = 0
12b - 2b + c = 0
10b + c = 0
c = - 10b
Уравнение перпендикуляра CK имеет вид:
- 2bx + by + c = 0
- 2bx + by - 10b = 0
2x - y + 10 = 0
Точка K - пересечение прямых BM: x + 2y = 0 и CK: 2x - y + 10 = 0. Следовательно, для нахождения координат точки K необходимо решить систему уравнений:
x + 2y = 0; 2x - y + 10 = 0
x = -4; y = 2
 )
 )
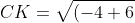^{2} + (2+2)^{2} } = \sqrt{4 + 16} = \sqrt{20} = 2\sqrt{5} )
Цитата: SSSergey написал 25 окт. 2009 23:34
4)координаты центра описанной около ABC окружности;
A(22; -6), B(-2; 1), C(-6; -2).
Пусть точка O - центр окружности, описанной около треугольника ABC. Известно, что центр описанной окружности - точка пересечения серединных перпендикуляров.
Построим первый серединный перпендикуляр h.
Возьмем сторону AC.
Точка M - середина стороны AC.
M (8; -4)
Построим перпендикуляр h к стороне AC, проходящий через точку M.
Пусть перпендикуляр h имеет своим уравнением выражение ax + by + c = 0.
Коэффициенты a, b и c необходимо определить.
Прямые h: ax + by + c = 0 и AC: x + 7y + 20 = 0 перпендикулярны. По условию перпендикулярности двух прямых
a + 7b = 0
a = - 7b
Уравнение прямой h имеет вид:
ax + by + c = 0
- 7bx + by + c = 0
Точка M (8; -4) лежит на прямой h. Следовательно, координаты точки M удовлетворяют уравнению прямой h:
- 7b*8 + b*(-4) + c = 0
- 56b - 4b + c = 0
- 60b + c = 0
c = 60b
Уравнение первого серединного перпендикуляра h примет вид:
- 7bx + by + c = 0
- 7bx + by + 60b = 0
7x - y - 60 = 0
Построим второй серединный перпендикуляр l.
Возьмем сторону BC.
Точка L - середина стороны BC.
B (-2; 1)
C (-6; -2)
L (-4; - 0.5)
Построим перпендикуляр l к стороне BC, проходящий через точку L.
Пусть перпендикуляр l имеет своим уравнением выражение ax + by + c = 0.
Коэффициенты a, b и c необходимо определить.
Прямые l: ax + by + c = 0 и BC: 3x - 4y + 10 = 0 перпендикулярны. По условию перпендикулярности двух прямых
3a - 4b = 0
4b = 3a
b = 3a/4
Уравнение прямой l имеет вид:
ax + by + c = 0
ax + 3ay/4 + c = 0
4ax + 3ay + 4c = 0
Точка L (-4; -0.5) лежит на прямой l. Следовательно, координаты точки L удовлетворяют уравнению прямой l:
4a*(-4) + 3a*(-0.5) + 4c = 0
- 16a - 1.5a + 4c = 0
- 17.5a + 4c = 0
4c = 17.5a
Уравнение второго серединного перпендикуляра l примет вид:
4ax + 3ay + 4c = 0
4ax + 3ay + 17.5a = 0
4x + 3y + 17.5 = 0
8x + 6y + 35 = 0
Для того, чтобы найти координаты точки O, необходимо решить систему уравнений:
7x - y - 60 = 0; 8x + 6y + 35 = 0
x = 6.5; y = - 14.5
O (6.5; -14.5)
Цитата: SSSergey написал 25 окт. 2009 23:34
5)угол между стороной AB и высотой, проведенной из вершины A;
A(22; -6), B(-2; 1), C(-6; -2).
Точка H является точкой пересечения прямых AH: 4x+3y-70=0 и BC: 3x-4y+10 = 0. Следовательно, для нахождения координат точки H необходимо решить систему уравнений:
4x + 3y - 70 = 0; 3x - 4y + 10 = 0
x = 10; y = 10
H (10; 10)
A (22; -6)
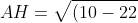^{2} + (10+6)^{2} } = \sqrt{144 + 256} = \sqrt{400} = 20 )
A (22; -6)
B (-2; 1)
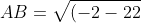^{2} + (1+6)^{2} } = \sqrt{576 + 49} = \sqrt{625} = 25 )
Рассмотрим треугольник ABH. Он является прямоугольным.
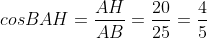
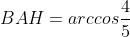
Цитата: SSSergey написал 25 окт. 2009 23:34
6)площадь треугольника.
A(22; -6), B(-2; 1), C(-6; -2).
B (-2; 1)
C (-6; -2)
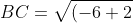^{2} + (-2-1)^{2} } = \sqrt{16 + 9} = \sqrt{25} = 5 )
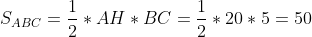
(Сообщение отредактировал attention 10 дек. 2009 15:04)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 26 окт. 2009 12:59 | IP
|
|
milavica

Новичок
|
     
Помогите решить пожалуйста!!!
Построить треугольник с вершинами A (7;4) B (6;-3) C(-6;3) и найти:
1) координаты точек пересечения медиан
2)длину и уравнение высоты, опущенной из верш. А
3)площадь треугольника
4)систему неравенств, задающих внутренность треугольника
Я начала решать но не знаю верно ли??? Подскажите привильно это?
1) координаты точек пересечения медиан:
Xo=(Xa+Xb+Xc)/3 x=2,33
Yo=(Ya+yb+yc)/3 y=1,33
2) уравнение стороны BС
x+2y=0
Н середина ВС её координаты получились (0;0)
уравнение высоты AH 4x-7y=0 правильно?
длину AH что-то не получается найти,
площадь тоже почему-то с минусом получилась. Помогите пжлст!
(Сообщение отредактировал milavica 26 окт. 2009 15:44)
|
Всего сообщений: 4 | Присоединился: октябрь 2009 | Отправлено: 26 окт. 2009 13:46 | IP
|
|
oc


Новичок
|
      
Найти угол между прямой L и плоскостью S в пространстве, если: L=x-3/0=y/-2=z+11/4 a S=3y+z-7=0
заранее спасибо)))
(Сообщение отредактировал attention 10 дек. 2009 15:05)
|
Всего сообщений: 8 | Присоединился: октябрь 2009 | Отправлено: 26 окт. 2009 16:08 | IP
|
|
Cardiff


Новичок
|
     
Даны две точки;A, лежащая на оси ординат, и B (1;0;1).Прямая AB состовляет с плоскостью Оxz угол в 30 градусов.Найдите координаты точки А.
Найдите координаты вектора a ,коллинеарного вектору b(6;8;-7,5) и образующий тупой угол с координатным вектором j ,если |a|=50
(Сообщение отредактировал attention 10 дек. 2009 15:06)
|
Всего сообщений: 17 | Присоединился: октябрь 2009 | Отправлено: 26 окт. 2009 16:31 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: milavica написал 26 окт. 2009 13:46
Построить треугольник с вершинами A (7;4) B (6;-3) C(-6;3) и найти:
1) координаты точек пересечения медиан
Пусть AM - медиана, опущенная из вершины A.
Точка M является серединой отрезка BC.
 )
 )
 )
 )
 )
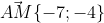
Уравнение медианы AM имеет вид:
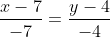
 = 7(y-4) )
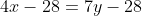
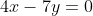
Пусть BK - медиана, опущенная из вершины B.
Точка K является серединой отрезка AC.
 )
 )
 )
 )
 )
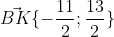
Уравнение медианы BK имеет вид:
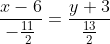
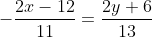
 = 11(2y + 6) )
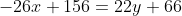
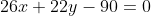

Для того, чтобы найти точку пересения медиан, необходимо решить систему уравнений:
4x - 7y = 0; 13x + 11y - 45 = 0
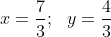
Цитата: milavica написал 26 окт. 2009 13:46
Построить треугольник с вершинами A (7;4) B (6;-3) C(-6;3) и найти:
2)длину и уравнение высоты, опущенной из верш. А
 )
 )

Уравнение стороны BC имеет вид:

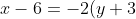 )
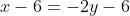
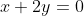
Пусть AH - высота, опущенная из вершины A.
Пусть уравнение высоты AH имеет вид: ax + by + c = 0.
Коэффициенты a, b и c необходимо определить.
Прямые AH: ax + by + c = 0 и BC: x + 2y = 0 перпендикулярны. По условию перпендикулярности двух прямых:
a + 2b = 0
a = - 2b
Уравнение высоты AH принимает вид:
ax + by + c = 0
- 2bx + by + c = 0
Точка A (7; 4) лежит на прямой AH. Следовательно, координаты точки A удовлетворяют уравнению прямой AH:
- 2b*7 + b*4 + c = 0
- 14b + 4b + c = 0
- 10b + c = 0
c = 10b
Уравнение высоты AH имеет вид:
- 2bx + by + c = 0
- 2bx + by + 10b = 0
- 2x + y + 10 = 0
2x - y - 10 = 0.
Точка H является точкой пересечения прямых AH и BC. Для нахождения координат точки H необходимо решить систему уравнений:
2x - y - 10 = 0; x + 2y = 0
x = 4; y = - 2
H (4; -2)
Цитата: milavica написал 26 окт. 2009 13:46
3)площадь треугольника
 )
 )
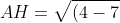^{2} + (-2-4)^{2} } = \sqrt{9 + 36} = \sqrt{45} )
 )
 )
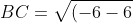^{2} + (3+3)^{2} } = \sqrt{144 + 36} = \sqrt{180} )
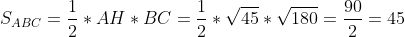
Цитата: milavica написал 26 окт. 2009 13:46
Построить треугольник с вершинами A (7;4) B (6;-3) C(-6;3) и найти:
4)систему неравенств, задающих внутренность треугольника
Уравнение стороны BC имеет вид: x + 2y = 0.
В левую часть уравнения подставляем координаты точки A (7;4): 7 + 2*4 = 7 + 8 = 15 > 0.
Таким образом, первое неравенство системы имеет вид: x + 2y > 0.
 )
 )
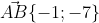
Уравнение стороны AB имеет вид:
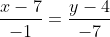
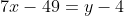
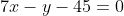
В левую часть уравнения подставляем координаты точки C (-6;3): 7*(-6) - 3 - 45 = -90 < 0.
Таким образом, второе неравенство системы имеет вид: 7x - y - 45 < 0.
 )
 )
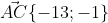
Уравнение стороны AC имеет вид:
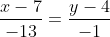
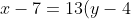 )
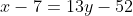
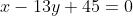
В левую часть уравнения подставляем координаты точки B (6; -3): 6 - 13*(-3) + 45 = 6 + 39 + 45 = 90 > 0.
Таким образом, третье неравенство системы имеет вид: x - 13y + 45 > 0.
Ответ. x + 2y > 0; 7x - y - 45 < 0; x - 13y + 45 > 0.
Цитата: oc написал 26 окт. 2009 16:08
найти угол между прямой L и плоскостью S в пространстве, если: L=x-3/0=y/-2=z+11/4 a S=3y+z-7=0

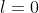
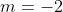
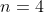
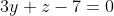
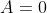
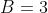
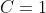

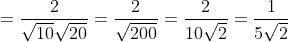
(Сообщение отредактировал attention 10 дек. 2009 15:13)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 26 окт. 2009 18:49 | IP
|
|
milavica

Новичок
|
     
RKI, спасибо большое!!!!!!!!!
|
Всего сообщений: 4 | Присоединился: октябрь 2009 | Отправлено: 26 окт. 2009 20:02 | IP
|
|
Yoh


Новичок
|
      
Из начала координат опустить перпендикуляр на прямую
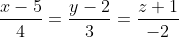
Заранее спс.
(Сообщение отредактировал attention 10 дек. 2009 15:16)
|
Всего сообщений: 3 | Присоединился: октябрь 2009 | Отправлено: 26 окт. 2009 20:06 | IP
|
|
Cardiff


Новичок
|
     
Пожалуйста!Срочно решить 2 задачи на завтра!Заранее всем спасибки!!!!!!!!!!
1)Даны две точки;A, лежащая на оси ординат, и B (1;0;1).Прямая AB состовляет с плоскостью Оxz угол в 30 градусов.Найдите координаты точки А.
2)Найдите координаты вектора a ,коллинеарного вектору b(6;8;-7,5) и образующий тупой угол с координатным вектором j ,если |a|=50
|
Всего сообщений: 17 | Присоединился: октябрь 2009 | Отправлено: 27 окт. 2009 13:24 | IP
|
|
oc


Новичок
|
      
Спасибо огромное)))
|
Всего сообщений: 8 | Присоединился: октябрь 2009 | Отправлено: 27 окт. 2009 13:50 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 2.9.1 Аналитическая геометрия
2.9.1 Аналитическая геометрия

 Форум
Форум

 Математика
Математика

 2.9.1 Аналитическая геометрия
2.9.1 Аналитическая геометрия