MargoA


Новичок
|
      
Помогите решить систему уравнений методом Гауса
х + у - 3z = -1
2x + y - 2z = 1
x + y + z = 3
x + 2y - 3z = 1
Почему 3 неизвестных и 4 уравнения???
|
Всего сообщений: 1 | Присоединился: октябрь 2009 | Отправлено: 24 окт. 2009 0:51 | IP
|
|
pavzer


Новичок
|
     
подскажите пожайлуста, какой граффик у данной функции:
y^2=(-3/4)x^2-x/2+1/4 в декартовой прямоугольной системе координат
|
Всего сообщений: 4 | Присоединился: октябрь 2009 | Отправлено: 24 окт. 2009 6:03 | IP
|
|
allash

Новичок
|
     
увыжаемые математики, почему в круге 360 градусов? спрашивает сын, ученик 4 класа школы, а я не знаю, что ответить))) помогите, уверена, что уж Вы то знаете точно правильный ответ.
|
Всего сообщений: 2 | Присоединился: октябрь 2009 | Отправлено: 24 окт. 2009 20:21 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: allash написал 24 окт. 2009 20:21
увыжаемые математики, почему в круге 360 градусов? спрашивает сын, ученик 4 класа школы, а я не знаю, что ответить))) помогите, уверена, что уж Вы то знаете точно правильный ответ.
внешняя ссылка удалена
Почитайте здесь
Очень интересно изложение
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 24 окт. 2009 20:34 | IP
|
|
allash

Новичок
|
     
спасибо, это забавное интересное объяснение)))
а если серьезно и научно, то как это объясняет геометрия, почему 360, а не 400,500 и.т.д
|
Всего сообщений: 2 | Присоединился: октябрь 2009 | Отправлено: 24 окт. 2009 21:14 | IP
|
|
RKI 


Долгожитель
|
     
Это и есть серьезное объяснение.
Объяснения, основанного на точных закономерностях, неких правилах , нет.
Современная геометрия взяла за основу эту модель - в круге 360 градусов.
И далее всё развитие строилось на этом.
Аналогия - была принята аксиома, что параллельные прямые не пересекаются.
Можно было брать другую модель - например, в круге 500 градусов. Но это было бы неудобно для вычислений.
Аналогия - Лобачевский (если я не ошибаюсь) ввел модель, что параллельные прямые пересекались.
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 24 окт. 2009 21:27 | IP
|
|
Cardiff


Новичок
|
     
Пожалуйста!!!
1)В кубе ABCDA1B1C1D1 длина ребра равна 1,М-центр грани DD1C1C.Используя метод координат найдите расстояние между серединами отрезков AM и B1D.
2)Даны две точки;A, лежащая на оси ординат, и B (1;0;1).Прямая AB состовляет с плоскостью Оxz угол в 30 градусов.Найдите координаты точки А.
|
Всего сообщений: 17 | Присоединился: октябрь 2009 | Отправлено: 25 окт. 2009 18:06 | IP
|
|
SSSergey


Новичок
|
     
Помогите решите пожалуйста ещё матричное исчисление

и
1)уравнение сторон треугольника;
2)уравнение высоты, проведенной из вершины A;
3)расстояние от вершины C до медианы, проведенной из вершины B;
4)координаты центра описанной около ABC окружности;
5)угол между стороной AB и высотой, проведенной из вершины A;
6)площадь треугольника.
A(22; -6), B(-2; 1), C(-6; -2).
спасибо!
|
Всего сообщений: 27 | Присоединился: октябрь 2009 | Отправлено: 25 окт. 2009 23:34 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Cardiff написал 25 окт. 2009 18:06
1)В кубе ABCDA1B1C1D1 длина ребра равна 1,М-центр грани DD1C1C.Используя метод координат найдите расстояние между серединами отрезков AM и B1D.
Пусть дан куб 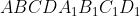 . .
Проведем декартову систему координат следующим образом: начало координат - точка A; ось Ox проходит через сторону 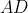 ; ось Oy проходит через сторону ; ось Oy проходит через сторону 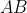 ; ось Oz проходит через сторону ; ось Oz проходит через сторону 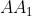 . .
По условию задачи длина ребра куба равна 1. Следовательно, вершины куба имеют следующие координаты:
 )
 )
 )
 )
 )
 )
 )
 )
Пусть точка K - середина отрезка 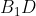 . Тогда . Тогда
 )
 )
Точка M - центр грани 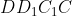 . Следовательно, . Следовательно,  )
Пусть точка L - середина отрезка AM. Тогда
 )
 )
^{2} + (0.5-0.25)^{2} + (0.5-0.25)^{2} } = \sqrt{0 + 0.0625 + 0.0625} = )
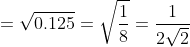
Цитата: SSSergey написал 25 окт. 2009 23:34
Помогите решите пожалуйста ещё матричное исчисление

Решить любым способом или каким-то конкретным?
(Сообщение отредактировал attention 10 дек. 2009 15:01)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 26 окт. 2009 11:55 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: SSSergey написал 25 окт. 2009 23:34
1)уравнение сторон треугольника;
A(22; -6), B(-2; 1), C(-6; -2).
 )
 )
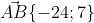
Уравнение стороны AB имеет вид:
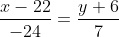
 = 24(y+6) )
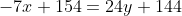
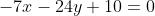
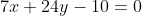
 )
 )
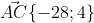
Уравнение стороны AC имеет вид:
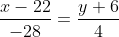
 = 7(y+6) )
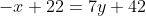
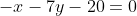
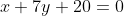
 )
 )
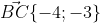
Уравнение стороны BC имеет вид:
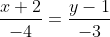
 = 4(y-1) )
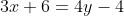
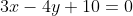
Цитата: SSSergey написал 25 окт. 2009 23:34
2)уравнение высоты, проведенной из вершины A;
A(22; -6), B(-2; 1), C(-6; -2).
Проведем высоту AH, где точка H лежит на прямой BC.
Пусть уравнение высоты AH имеет вид ax + by + c = 0. Коэффициенты a, b и c необходимо определить.
Прямые AH: ax + by + c = 0 и BC: 3x - 4y + 10 = 0 перпендикулярны. По условию перпендикулярности двух прямых:
3a - 4b = 0
4b = 3a
b = 3a/4
Уравнение высоты AH примет следующий вид:
ax + by + c = 0
ax + (3a/4)y + c = 0
4ax + 3ay + 4c = 0.
Точка A (22; -6) лежит на прямой AH. Значит, координаты точки A удовлетворяют уравнению высоты AH:
4a*22 + 3a*(-6) + 4c = 0
88a - 18a + 4c = 0
70a + 4c = 0
4c = - 70a
Таким образом, уравнение высоты AH принимает вид:
4ax + 3ay + 4c = 0
4ax + 3ay - 70a = 0
4x + 3y - 70 = 0
(Сообщение отредактировал attention 10 дек. 2009 15:02)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 26 окт. 2009 12:28 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 2.9.1 Аналитическая геометрия
2.9.1 Аналитическая геометрия

 Форум
Форум

 Математика
Математика

 2.9.1 Аналитическая геометрия
2.9.1 Аналитическая геометрия