MEHT


Долгожитель
|
     
Когда избавляетесь от корня, квадрат игрека будет положительным:
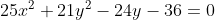
Вам осталось выделить из игреков полный квадрат и представить полученную конструкцию в каноническом виде
^2=%5Cfrac{300}{7}%5Cleft, )
^2}&space; +&space; %5Cfrac{%5Cleft&space; (&space;y-%5Cfrac{4}{7}&space; %5Cright&space; )^2}{%5Cleft&space;(&space;%5Cfrac{10}{7}&space; %5Cright&space; )^2}&space;=&space; 1. )
(Сообщение отредактировал MEHT 31 дек. 2011 1:20)
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 31 дек. 2011 1:17 | IP
|
|
facons

Новичок
|
      
Помогите решить...
Даны координаты вершин пирамиды А1А2А3А4: А1(3,3,8), А2(6,9,0), А3(1,7,2), А4(8,5,7). Найти:
1) Длинну ребра А1А2.
2)угол между ребрами А1А2 и А1А4.
3) угол между ребром А1А4 и гранью А1А2А3.
4) площадь грани А1А2А3.
5) объем пирамиды.
6) уравнение прямой А1А2
7) уравнение плоскости А1А2А3. Сделать чертеж.
(Сообщение отредактировал facons 8 янв. 2012 16:02)
|
Всего сообщений: 3 | Присоединился: январь 2012 | Отправлено: 8 янв. 2012 15:56 | IP
|
|
sebuble

Новичок
|
     
внешняя ссылка удалена
|
Всего сообщений: 1 | Присоединился: январь 2012 | Отправлено: 14 янв. 2012 15:23 | IP
|
|
swetlang

Новичок
|
     
Запуталась с каноническим уравнением. :cry:
Исходные данные: Привести к каноническому виду
2y^2-6y-9x-8.5=0
находим коэффициенты:
а11=0
а12=0
а22=2
а1=-4,5
а2=-3
а0=-8,5
т.к. а12=0, то уравнение имеет "почти" приведенный вид. Поэтому полагаем, что S=E.
выделяем полный квадрат по y:
(2y^2-6y+9)-9-9x-8.5=0
(2^(1/2)y-3)^2-9x-17.5=0
А дальше застряла :oops:
(Сообщение отредактировал swetlang 29 янв. 2012 1:00)
|
Всего сообщений: 12 | Присоединился: апрель 2011 | Отправлено: 29 янв. 2012 0:35 | IP
|
|
Katja

Новичок
|
     
Здравствуйте. Подскажите пожалуйста, как записать параметрические уравнения поверхности, образованной вращением кривой y=f(x) вокруг оси Oy.
|
Всего сообщений: 1 | Присоединился: февраль 2012 | Отправлено: 21 фев. 2012 18:11 | IP
|
|
Alenka9921

Новичок
|
      
Написать разложение вектора x по векторам а,в,с: х= (1,-4,4) ,а=(2,1,-1), в=(0,3,2), с=(1,-1,1)
|
Всего сообщений: 4 | Присоединился: март 2012 | Отправлено: 6 марта 2012 15:20 | IP
|
|
kahraba

Долгожитель
|
     
Alenka9921, составим систему уравнений:
2x+0y+z=1
x+3y-z=-4
-x+2y+z=4
cложим (2) и (3)
3y+2y=0 5y=0 y=0
cложим (1) и (2) учитывая, что у=0
2х+х=-3 3х=-3 х=-1
подставим значение (х) в (1) -2+0+z=1 z=3
записываем разложенный вектор: х= -1*а+0*b+3*c= -a+3c
x= -a+3c
|
Всего сообщений: 896 | Присоединился: август 2011 | Отправлено: 9 марта 2012 9:17 | IP
|
|
Alenka9921

Новичок
|
      
Коллинеарны ли векторы С1,С2, построенные по векторам а,в? а=(-2,4,1), в=(1,-2,7), с1=5а+3в, с2=2а-в
|
Всего сообщений: 4 | Присоединился: март 2012 | Отправлено: 13 марта 2012 12:29 | IP
|
|
miss fox


Новичок
|
       
Помогите помогите помогите пожалуйста!!! 1 график остался я капец как с ним замучилась, ни чего не понимаю x^2+8x-9y-29=0 нужно привести к каноническому виду и построить график, я вроде как привела но она утверждает что не так и ещё требует найти вершину а я не понимаю как, помогите буду благодарна))
|
Всего сообщений: 3 | Присоединился: январь 2012 | Отправлено: 14 марта 2012 20:34 | IP
|
|
MEHT


Долгожитель
|
     
^2-9%5Cleft%20(y+5%20%5Cright%20)=0;%5C%5C%5C%5C%20x'=y+5,%5C%5C%20y'=x+4,%5C%5C%20%5C%5C%20y'^2=2%5Ccdot%20%5Cleft%20(%5Cfrac{9}{2}%20%5Cright%20)%5Ccdot%20x')
В штрихованных координатах парабола задана канонически.
Вершина параболы - начало координат в этих самых штрихованных координатах. Приравняете к нулю x' и y', найдёте из вышезаписанных преобразований координаты вершины в XOY (фактически устный счёт).
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 15 марта 2012 16:14 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 2.9.1 Аналитическая геометрия
2.9.1 Аналитическая геометрия

 Форум
Форум

 Математика
Математика

 2.9.1 Аналитическая геометрия
2.9.1 Аналитическая геометрия