ProstoVasya
Долгожитель
|
    
Рассмотрим случай |z-1+i|>корня из 2.
Сначала сделайте сдвиг и сжатие, отобразив Ваш круг на единичный с центром в нуле.
w = корень из 2/(z-1+i).
Затем единичный круг отобразите на верхнюю полуплоскость.
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 20 нояб. 2009 21:59 | IP
|
|
Rabbit
Новичок
|
Помогите, пожалуйста найти множество точек 
|
Всего сообщений: 4 | Присоединился: ноябрь 2009 | Отправлено: 29 нояб. 2009 18:31 | IP
|
|
Graf de la Kruf
Новичок
|
Помогите плиз решить!!!
Найти все значения корня из комплексного числа. Сделать чертеж.
Корень 3-ей степени из (i/27).
|
Всего сообщений: 25 | Присоединился: август 2009 | Отправлено: 30 нояб. 2009 11:02 | IP
|
|
Black_Star
Участник
|
  
Цитата: ProstoVasya написал 3 нояб. 2009 17:36
Black Star
Можете пожалуйста, объяснить болие подробно откуда берётся  А то я ни как не могу придумать той формулы которую Вы используете
|
Всего сообщений: 109 | Присоединился: ноябрь 2007 | Отправлено: 7 дек. 2009 23:55 | IP
|
|
attention 
Долгожитель
|
Цитата: Black Star написал 7 дек. 2009 22:55
Цитата: ProstoVasya написал 3 нояб. 2009 17:36
Black Star
Можете пожалуйста, объяснить болие подробно откуда берётся А то я ни как не могу придумать той формулы которую Вы используете
Black Star, рассмотрите как обычное уравнение относительно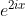 
(1 - 2i)}{(1 + 2i)(1 - 2i)} = \frac{2i + 4 - 4 + 8i}{1 + 4} = \frac{10i}{5} = 2i. \hfill \\ \end{gathered})
(Сообщение отредактировал attention 8 дек. 2009 0:50)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 8 дек. 2009 1:47 | IP
|
|
Black_Star
Участник
|
attention, спасибо.
|
Всего сообщений: 109 | Присоединился: ноябрь 2007 | Отправлено: 8 дек. 2009 22:11 | IP
|
|
Novenkaya1
Новичок
|
Помогите пожалуйста
разложить функцию в ряд Лорана в кольце sqrt(5)<|z-1|<3 , и в окрестности точки z=-2
f(z)=1/(z+2)(z^2+4)
совсем непонятно как решать
раскладываем ф-цию по степеням (z+2):
1/(z+2)(z^2+4) =1/((z+2)((z+2)^2-4z))= 1/((z+2)^3(1-4z/(z+2)^2))
как теперь избавится от z в числителе дроби 4z/(z+2)^2 чтобы можно было разложить ф-цию по формуле 1/1-x ?
(Сообщение отредактировал attention 9 дек. 2009 23:11)
|
Всего сообщений: 16 | Присоединился: май 2009 | Отправлено: 9 дек. 2009 18:23 | IP
|
|
attention
Долгожитель
|
Novenkaya1, не дублируйте посты! Вам помогут.
Лучше покажите, что у вас получилось решить, до чего дошли, что именно не получается.
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 9 дек. 2009 18:58 | IP
|
|
Kuonna
Новичок
|
помогите пожалуйста
нужно:
-разложить функцию в ряд Лорана по степеням z
z^2
f(z)= ----------
(z+1)^2
-найти разложение функции в ряд Лорана по степеням z-i и указать главную и правильную части ряда.
f(z)=e^(z/(z-i))
-найти все вычеты функции
f(z)=e^(z/(1-z))
-найти все особые точки и установить их тип
1
f(z)=--------------------------
(z^3)*(((z^2)+4)^2)
ОЧЕНЬ НУЖНА ВАША ПОМОЩЬ!!!
заранее благодарна)
(Сообщение отредактировал Kuonna 13 дек. 2009 2:54)
|
Всего сообщений: 1 | Присоединился: декабрь 2009 | Отправлено: 13 дек. 2009 2:29 | IP
|
|
Nord
Новичок
|
Помогите, пожалуйста, решить такой интеграл:
интегрирование от 0 до +беск. функция:
[ (ln(x))^2 * dx] / [ (x^2+1)^2 ]
Здесь функция действительной переменной, но надо решить методами ТФКП.
Как вообще решать несобственные интегралы второго рода в ТФКП? (про первый род написано в учебнике Свешникова)
|
Всего сообщений: 8 | Присоединился: май 2009 | Отправлено: 20 дек. 2009 21:29 | IP
|
|
Форум
2.2.2 Теория функций комплексного переменного (ТФКП)
