Roman Osipov 
Долгожитель
|
        
Функциональные ряды: теория и конкретные примеры.
Для вопросов сходимости есть соотв. тема!
|
Всего сообщений: 2356 | Присоединился: май 2007 | Отправлено: 19 апр. 2009 14:13 | IP
|
|
Njutochka27
Новичок
|
Здравствуйте!!! Помогите, пожалуйста!!!
Разложить функцию в ряд Маклорена,
определить область сходимости ряда
а) f(3x^2*cos(2x))
б) f(5/(4-3x))
у меня получилось так:
а) f(3x^2*cos(2x))=6x^2/2!-144x^4/4!+1824x^6/6!+...
даже не знаю, верно или нет, а дальше совсем запуталась
б) f(5/(4-3x))=(5/4*3x/4)+(5/4*3x^2/4^2)+(5/4*3x^3/4^3)+...
x принадлежит (-4/3;4/3)
|
Всего сообщений: 26 | Присоединился: сентябрь 2009 | Отправлено: 1 окт. 2009 11:37 | IP
|
|
Njutochka27
Новичок
|
Помогите, пожалуйста, буду очень признательна!!!
Разложить функцию в ряд Маклорена,
определить область сходимости ряда
f(3x^2*cos(2x))
|
Всего сообщений: 26 | Присоединился: сентябрь 2009 | Отправлено: 5 окт. 2009 15:23 | IP
|
|
Nissa
Новичок
|
Подскажите, пожалуйста!
Есть задание - необходимо вычислить интеграл с заданной точностью - т.е. сначала разложить функцию в ряд.
Подинтегральная функция, которую у меня не получается разложить в ряд:
(81+x^4)^(-1/4)
|
Всего сообщений: 1 | Присоединился: декабрь 2011 | Отправлено: 23 дек. 2011 21:18 | IP
|
|
ustam
Долгожитель
|
Цитата: Nissa написал 23 дек. 2011 21:18
Подскажите, пожалуйста!
Есть задание - необходимо вычислить интеграл с заданной точностью - т.е. сначала разложить функцию в ряд.
Подинтегральная функция, которую у меня не получается разложить в ряд:
(81+x^4)^(-1/4)
(81+x^4)^(-1/4) = (1/3)*{[1+(x/3)^4]^(-1/4)}
Воспользуйтесь разложением в ряд функции (1+х)^a, где а=-1/4
Вместо (х) в этом ряду подставляете (x/3)^4, и весь полученный ряд умножаете на (1/3).
Ну, а дальше интегрируете
|
Всего сообщений: 420 | Присоединился: декабрь 2008 | Отправлено: 24 дек. 2011 1:48 | IP
|
|
wanes101
Новичок
|
Всем привет
не пойму как разложить в ряд Тейлора
Если известно:
Как разложить еще догадаюсь, используя формулу Тейлора, но с определением сходимости возникнет вопрос, т.к. мне не понятно для чего добавлено вот это условие:
(Сообщение отредактировал wanes101 22 марта 2013 5:48)
|
Всего сообщений: 13 | Присоединился: июнь 2012 | Отправлено: 22 марта 2013 5:46 | IP
|
|
mad_math
Новичок
|
Может имеется в виду использование стандартного разложения для функции  с последующим его интегрированием?
|
Всего сообщений: 19 | Присоединился: май 2012 | Отправлено: 24 марта 2013 0:16 | IP
|
|
mad_math
Новичок
|
Может имеется в виду использование стандартного разложения для функции 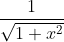 с последующим его интегрированием?
|
Всего сообщений: 19 | Присоединился: май 2012 | Отправлено: 24 марта 2013 0:17 | IP
|
|
katyasmirnovva
Новичок
|
1)Разложить по степеням х в ряд указанной функции. Указать интервал сходимости.
а) y=2^(-x)
б) y=x〖sinx〗^2
2)Вычислить указанный определенный интеграл взяв первые три члена разложения в ряд, и оценить полученную точность.
∫_0^0,5▒〖ln(1+x^3 )dx〗
3)Используя разложения функции в степенной ряд, вычислить ее значения с точностью до 〖10〗^(-4)
a)√(10&1026)
б)sin0.5
в)ln16
|
Всего сообщений: 1 | Присоединился: июнь 2016 | Отправлено: 16 июня 2016 13:34 | IP
|
|
Ancestor
Новичок
|
Привет, помогите пожалуйста разобраться с заданием:
С помощью разложения в ряд найти приближёно частное решение дифференциального уравнения (определить пять отличных от нуля членов разложения).
y' = y + x * (exp^y),y(0) = 0;
Я начал решать вот так:
1. y' = y + x * (exp^y) = 0 + 0*1 = 0;
2. y'' = ( y + x * (exp^y) )' = y' + exp^y + x * (exp^y) * y' = 0 + 1 + 0 * 1 = 1;
3. y''' = ( y' + exp^y + x * (exp^y) * y' )' = y'' + (exp^y) * y' + (exp^y) * y' + x * ( (exp^y)' * y' + (exp^y) * y' ) =
= y'' + (exp^y) * y' + (exp^y) * y' + x * ( exp^y * y' * y' + (exp^y) * y'' ) = 1 + 0 + 0 + 0 = 1;
У меня возникло сомнение, правильно ли я взял производную на третьем этапе: ( x * (exp^y) * y' )' = ?
(Сообщение отредактировал Ancestor 4 дек. 2016 15:50)
(Сообщение отредактировал Ancestor 4 дек. 2016 20:07)
|
Всего сообщений: 1 | Присоединился: декабрь 2016 | Отправлено: 3 дек. 2016 13:06 | IP
|
|
Форум
2.1.16 Функциональные ряды
