venom11


Новичок
|
      
У меня вот такой вопрос:а всё что касается кривых второго порядка,сюда писать?Или в другую тему?
|
Всего сообщений: 7 | Присоединился: сентябрь 2009 | Отправлено: 26 сен. 2009 16:13 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: venom11 написал 26 сен. 2009 16:13
У меня вот такой вопрос:а всё что касается кривых второго порядка,сюда писать?Или в другую тему?
Можно и сюда
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 26 сен. 2009 18:25 | IP
|
|
venom11


Новичок
|
      
Вот такие задания:
Задания перевожу с украинского.Слова,которые не могу перевести буду писать в квадратных скобках.
1)Найти точку пересечения оси Оу с [колом],диаметром которого является отрезок,который соединяет точки (-1;1) и (-2;-3).
2)Составить уравнение элипса,фокусы которого лежат на оси абсцис,симетрично относительно начала координат,если задано точка М1 (8;12) элипса и расстояние r1=20 [від її до ливого фокуса].
3)Составить уравнение гиперболы,фокусы которой расположены на оси ординат симетрично относительно начала координат,зная уравнение [асимптот] у=+- 12/5х и расстояние между вершинами равняется 48.
4)Составить уравнение параболы,вершина которой совпадает с началом координат,зная,что парабола расположена симетрично относительно оси Оу и проходит через точку D (4;-8).
Если нужно, могу полностью на украинском,как оно есть,задание написать.
(Сообщение отредактировал attention 10 дек. 2009 14:47)
|
Всего сообщений: 7 | Присоединился: сентябрь 2009 | Отправлено: 27 сен. 2009 1:21 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: venom11 написал 27 сен. 2009 1:21
1)Найти точку пересечения оси Оу с [колом],диаметром которого является отрезок,который соединяет точки (-1;1) и (-2;-3).
Рассматриваю следующую задачу. Найти точку пересечения оси Оу с кругом ,диаметром которого является отрезок,который соединяет точки (-1;1) и (-2;-3).
 )
 )
Отрезок AB является диаметром.
Пусть точка O является центром круга. Следовательно, точка O - середина отрезка AB.
 )
 )
Посчитаем длину диаметра AB.
^2 + (-3-1)^2} = \sqrt{1+16} = \sqrt{17} )
Тогда радиус круга AO равен
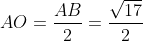
Тогда уравнение указанного в задаче круга имеет вид:
^2 + (y + 1)^2 \le \frac{17}{4} )
Найдем точки пересечения круга с осью Oy, то есть точки круга, абсциссы которых равны нулю.
^2 + (y + 1)^2 \le \frac{17}{4} )
^2 \le \frac{17}{4} )
^2 \le 2 )

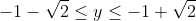
Ответ. : -1-\sqrt{2} \le y \le -1+\sqrt{2} \} )
Цитата: venom11 написал 27 сен. 2009 1:21
1)Найти точку пересечения оси Оу с [колом],диаметром которого является отрезок,который соединяет точки (-1;1) и (-2;-3).
Рассматриваю следующую задачу. Найти точку пересечения оси Оу с окружностью ,диаметром которой является отрезок,который соединяет точки (-1;1) и (-2;-3).
 )
 )
Отрезок AB является диаметром.
Пусть точка O является центром окружности. Следовательно, точка O - середина отрезка AB.
 )
 )
Посчитаем длину диаметра AB.
^2 + (-3-1)^2} = \sqrt{1+16} = \sqrt{17} )
Тогда радиус окружности AO равен
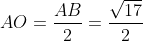
Тогда уравнение указанной в задаче окружности имеет вид:
^2 + (y + 1)^2 = \frac{17}{4} )
Найдем точки пересечения окружности с осью Oy, то есть точки окружности, абсциссы которых равны нулю.
^2 + (y + 1)^2 = \frac{17}{4} )
^2 = \frac{17}{4} )
^2 = 2 )
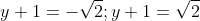
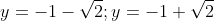
Ответ. ; (0;-1+\sqrt{2}) )
Цитата: venom11 написал 27 сен. 2009 1:21
4)Составить уравнение параболы,вершина которой совпадает с началом координат,зная,что парабола расположена симетрично относительно оси Оу и проходит через точку D (4;-8).
По условию задачи парабола расположена симметрично относительно оси Oy. Следовательно, уравнение параболы имеет вид:
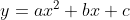
Координаты вершины параболы вычисляются по формулам:
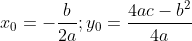
По условию задачи вершина параболы совпадает с началом координат. Следовательно,
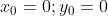
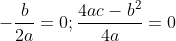
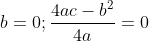
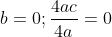
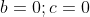
Следовательно, уравнение параболы имеет вид:
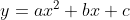
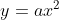
Парабола проходит через точку D (4;-8). Следовательно, координаты точки D удовлетворяют уравнению параболы:
 )
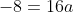
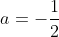
Уравнение параболы имеет вид:
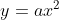
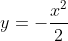
(Сообщение отредактировал attention 10 дек. 2009 14:48)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 27 сен. 2009 10:33 | IP
|
|
kibdaria

Новичок
|
     
Можно ещё вот такую задачку!!! записать уравнение прямой в канонической форме 2х-3у+2z+2=0; х+3у+z+1=0
и 2) Привести квадратичную форму к каноническому виду xy+yz+xz.
Пожалуйста помогите!!!!!!
|
Всего сообщений: 4 | Присоединился: сентябрь 2009 | Отправлено: 27 сен. 2009 11:04 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: venom11 написал 27 сен. 2009 1:21
3)Составить уравнение гиперболы,фокусы которой расположены на оси ординат симетрично относительно начала координат,зная уравнение [асимптот] у=+- 12/5х и расстояние между вершинами равняется 48.
Рассматриваем гиперболу, фокусы которой расположены на оси ординат симметрично относительно начала координат.
Следовательно,
1) вершины гиперболы также расположены на оси ординат симметрично относительно начала координат.
a - расстояние от начала координат до одной из вершин
2a = 48
a = 24
2) уравнения асимптот гиперболы имеют вид:
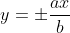
В случае данной задачи
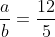
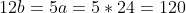
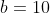
3) уравнение гиперболы имеет вид:
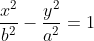

Цитата: kibdaria написал 27 сен. 2009 11:04
записать уравнение прямой в канонической форме 2х-3у+2z+2=0; х+3у+z+1=0
Задано уравнение прямой как пересечение двух плоскостей:
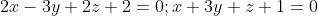
Найдем точку, лежащую на данной прямой.
Положим z = 0. Для нахождения абсциссы и ординаты точки необходимо решить систему линейных уравнений:
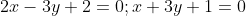
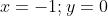
Таким образом, точка A (-1;0;0) - точка, лежащая на заданной прямой.
Найдем напрвляющий вектор прямой:
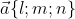
l = |-3 2| = (-3)*1 - 2*3 = - 3 - 6 = - 9
|3 1|
m = |2 2| = 2*1 - 2*1 = 2 - 2 = 0
|1 1|
n = |2 -3| = 2*3 - (-3)*1 = 6 + 3 = 9
|1 3|
Данные формулы можно посмотреть здесь: внешняя ссылка удалена
Направляющий вектор имеет вид:
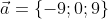
Каноническое уравнение прямой имеет вид:
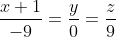
Цитата: kibdaria написал 27 сен. 2009 11:04
2) Привести квадратичную форму к каноническому виду xy+yz+xz.
f(x,y,z) = xy + yz + xz
Матрица A квадратичной формы имеет вид
0 1/2 1/2
1/2 0 1/2
1/2 1/2 0
Найдем собственные значения a матрицы A
|-a 1/2 1/2| = (-a)*|-a 1/2| -(1/2)*|1/2 1/2| +(1/2)*|1/2 -a|
|1/2 -a 1/2| |1/2 -a| |1/2 -a | |1/2 1/2|
|1/2 1/2 -a|
= (-a)*(a^2 - 1/4) - (1/2)*(-a/2 - 1/4) + (1/2)*(1/4 + a/2) =
= - a^3 + a/4 + a/4 + 1/8 + 1/8 + a/4 =
= - a^3 + 3a/4 + 1/4 = 0
a1 = 1
a2 = - 1/2
Тогда канонический вид заданной квадратической формы имеет вид
 = x_{1}^2 - \frac{x_{2}^2}{2} )
(Сообщение отредактировал attention 10 дек. 2009 14:50)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 27 сен. 2009 12:50 | IP
|
|
kibdaria

Новичок
|
     
огромное вам спасибо!!!!!!!!!!!
|
Всего сообщений: 4 | Присоединился: сентябрь 2009 | Отправлено: 27 сен. 2009 14:26 | IP
|
|
arinka

Новичок
|
     
Вы можете мне помочь решить задачу : Даны вершины пирамиды А1 (2,2,7) А2 (7,7,5) А3( 1,3,5) А4 (-1,5,1) Найти: 1) длину ребра А1,А2. 2) угол между рёбрами А1,А2 и А1,А3. 3) площадь грани А1,А2,А3. 4) объём пирамиды. 5) угол между ребромА1,А4 и гранью А1,А2,А3. 6) уравнение прямой А1,А2. 7) уравнение плоскости А1,А2,А3. 8) уравнение высоты к плоскости А1,А2,А3 проходящего через точку А4. 10) убедиться, что точка А4 принадлежит плоскости А1,А2,А3.
ПОМОГИТЕ ПОЖАЛУЙСТА!!!!!!!!!!!!
|
Всего сообщений: 2 | Присоединился: сентябрь 2009 | Отправлено: 27 сен. 2009 15:15 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: arinka написал 27 сен. 2009 15:15
1) длину ребра А1,А2.
 )
 )
^5 + (7-2)^2 + (5-7)^2} = \sqrt{25 + 25 + 4} = \sqrt{54} = 3\sqrt{6} )
Цитата: arinka написал 27 сен. 2009 15:15
2) угол между рёбрами А1,А2 и А1,А3.
 )
 )
 )
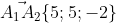
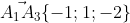
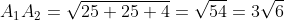
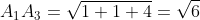
 = 5*(-1) + 5*1 + (-2)*(-2) = - 5 + 5 + 4 = 4 )
 = A_{1}A_{2} * A_{1}A_{3} * cos(A_{2}A_{1}A_{3}) = )
 = 18cos(A_{2}A_{1}A_{3}) )
 = 4 )
 = \frac{2}{9} )
 )
Цитата: arinka написал 27 сен. 2009 15:15
3) площадь грани А1,А2,А3.
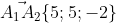
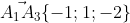
\vec{i} - (-10-2)\vec{j} + (5+5)\vec{k} = - 8\vec{i} + 12\vec{j} + 10\vec{k} )
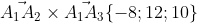
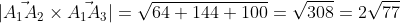
 = \frac{2\sqrt{77} }{2} = \sqrt{77} )
Цитата: arinka написал 27 сен. 2009 15:15
6) уравнение прямой А1,А2.
 )
 )
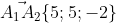
Уравение прямой 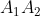 имеет вид: имеет вид:
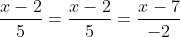
(Сообщение отредактировал attention 10 дек. 2009 14:55)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 27 сен. 2009 16:15 | IP
|
|
hfgeasd


Новичок
|
      
Пожалуйста,помогите решить две задачи!
1) В треугольнике ABC AB=9? BC=15. Из точки D,взятой на стороне AC,проведена прямая DE(точка E лежит на BC) так,что угол DEC=углу A. Найти DC, если DE=6.
2) В равнобедренный треугольник ABC(AB=BC)вписана окружность.Величина высоты BD,опущенной из вершины треугольникаравна 8см.Найти радиус вписанной окружности,если косинус угла A равен 3/5.
(Сообщение отредактировал attention 10 дек. 2009 14:55)
|
Всего сообщений: 32 | Присоединился: сентябрь 2009 | Отправлено: 28 сен. 2009 18:10 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 2.9.1 Аналитическая геометрия
2.9.1 Аналитическая геометрия

 Форум
Форум

 Математика
Математика

 2.9.1 Аналитическая геометрия
2.9.1 Аналитическая геометрия