MAcbka20

Новичок
|
      
При каком P плоскость треугольника ABC перпендикулярна плоскости треугольника ABD если заданы
A(-1;2;0) B(3;-2;1) C(1;1;-1) D(P;4;-2).
Заранее спасибо.
|
Всего сообщений: 4 | Присоединился: март 2010 | Отправлено: 3 марта 2010 17:19 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: MAcbka20 написал 3 марта 2010 17:19
При каком P плоскость треугольника ABC перпендикулярна плоскости треугольника ABD если заданы
A(-1;2;0) B(3;-2;1) C(1;1;-1) D(P;4;-2).
Заранее спасибо.
 )
 )
 )
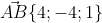

Уравнение плоскости  имеет вид: имеет вид:
|x+1 y-2 z| = 0
| 4 -4 1|
| 2 -1 -1|
(x+1)*|-4 1| - (y-2)*|4 1| + z*|4 -4| = 0
|-1 -1| |2 -1| |2 -1|
5(x+1) + 6(y-2) + 4z = 0
5x + 5 + 6y - 12 + 4z = 0
5x + 6y + 4z - 7 = 0 - уравнение плоскости 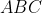
 )
 )
 )
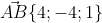
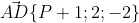
Уравнение плоскости 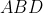 имеет вид: имеет вид:
|x+1 y-2 z| = 0
| 4 -4 1|
|P+1 2 -2|
(x+1)*|-4 1| - (y-2)*|4 1| + z*|4 -4| = 0
|2 -2| |P+1 -2| |P+1 2|
6(x+1) - (y-2)(-8-P-1) + z(8+4P+4) = 0
6(x+1) - (y-2)(-9-P) + z(12+4P) = 0
6(x+1) + (y-2)(9+P) + z(12+4P) = 0
6x + 6 + 9y + Py - 18 - 2P + 12z + 4Pz = 0
6x + (9+P)y + (12+4P)z - 12 - 2P = 0 - уравнение плоскости 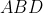
По условию перпендикулярности плоскостей
5*6 + 6*(9+P) + 4*(12+4P) = 0
30 + 54 + 6P + 48 + 16P = 0
22P + 132 = 0
P = -6
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 4 марта 2010 13:59 | IP
|
|
MAcbka20

Новичок
|
      
Спасибо ОГРОМНОЕ!
|
Всего сообщений: 4 | Присоединился: март 2010 | Отправлено: 4 марта 2010 21:01 | IP
|
|
Aubrey1

Новичок
|
        
пожалуйста помогите
Help me!!!!! please!!!!!!!!!!
Пирамида SABC задана вершинами S(5;6;-11), A(6;-6;-5), B(-6;6;-6), C(-6;-5;-11)
Найти
а) Уравнение плоскости проходящей через точки ABC
б) Величину угла между ребром SC и гранью ABC
в) площадь грани ABC
г) уравнение высоты опущеной из вершины S на грань ABC и её длинну
д) обьем пирамиды
|
Всего сообщений: 26 | Присоединился: март 2010 | Отправлено: 5 марта 2010 0:18 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Aubrey1 написал 5 марта 2010 0:18
Пирамида SABC задана вершинами S(5;6;-11), A(6;-6;-5), B(-6;6;-6), C(-6;-5;-11)
Найти
а) Уравнение плоскости проходящей через точки ABC
 )
 )
 )

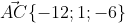
Уравнение плоскости 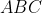 : :
|x-6 y+6 z+5| = 0
|-12 12 -1|
|-12 1 -6|
(x-6)*|12 -1| - (y+6)*|-12 -1| + (z+5)*|-12 12| = 0
| 1 -6| |-12 -6| |-12 1|
-71(x-6) - 60(y+6) + 132(z+5) = 0
-71x + 426 - 60y - 360 + 132z + 660 = 0
-71x - 60y + 132z + 726 = 0
71x + 60y - 132z - 726 = 0 - уравнение плоскости 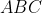
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 5 марта 2010 10:26 | IP
|
|
Aubrey1

Новичок
|
        
Спасибо огромное!!! этот пункт теперь понятен
|
Всего сообщений: 26 | Присоединился: март 2010 | Отправлено: 5 марта 2010 10:37 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Aubrey1 написал 5 марта 2010 0:18
Пирамида SABC задана вершинами S(5;6;-11), A(6;-6;-5), B(-6;6;-6), C(-6;-5;-11)
Найти
б) Величину угла между ребром SC и гранью ABC
 )
 )
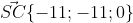
Уравнение прямой  имеет вид: имеет вид:
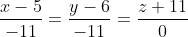
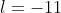
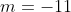
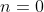
Уравнение плоскости 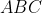 имеет вид: имеет вид:
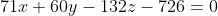
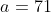
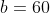
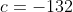
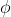 - угол между прямой - угол между прямой  и плоскостью и плоскостью 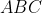

 + 60*(-11) + (-132)*0|}{\sqrt{5041 + 3600 + 17424}\sqrt{121 + 121 + 0} } = )

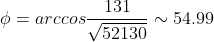
(Сообщение отредактировал RKI 5 марта 2010 10:42)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 5 марта 2010 10:39 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Aubrey1 написал 5 марта 2010 0:18
Пирамида SABC задана вершинами S(5;6;-11), A(6;-6;-5), B(-6;6;-6), C(-6;-5;-11)
Найти
в) площадь грани ABC

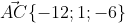
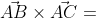
= | i j k| = i*|12 -1| - j*|-12 -1| + k*|-12 12| =
|-12 12 -1| | 1 -6| |-12 -6| |-12 1|
|-12 1 -6|
= -71i - 60j + 132k
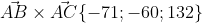
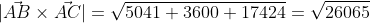
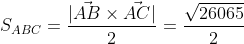
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 5 марта 2010 10:51 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Aubrey1 написал 5 марта 2010 0:18
Пирамида SABC задана вершинами S(5;6;-11), A(6;-6;-5), B(-6;6;-6), C(-6;-5;-11)
Найти
г) уравнение высоты опущеной из вершины S на грань ABC и её длинну
Обозначим  - высота пирамиды, где точка - высота пирамиды, где точка 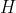 лежит на плоскости лежит на плоскости 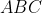
Уравнение высоты  имеет вид: имеет вид:
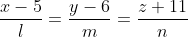
Прямая  перпендикулярна плоскости перпендикулярна плоскости 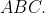 По условию перпендикулярности прямой и плоскости в просранстве: По условию перпендикулярности прямой и плоскости в просранстве:
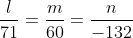
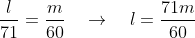

Уравнение прямой  имеет вид: имеет вид:
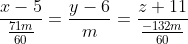
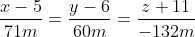
 - уравнение высоты - уравнение высоты 
(Сообщение отредактировал RKI 5 марта 2010 11:04)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 5 марта 2010 11:01 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Aubrey1 написал 5 марта 2010 0:18
г) уравнение высоты опущеной из вершины S на грань ABC и её длинну
 )
Найдем координаты точки 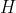
С одной стороны, точка 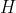 лежит на прямой лежит на прямой  . Следовательно, координаты точки . Следовательно, координаты точки 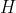 удовлетворяют уравнению прямой удовлетворяют уравнению прямой  : :
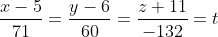
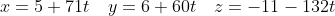
 )
С другой стороны, точка 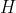 лежит на плоскости лежит на плоскости  Следовательно, координаты точки Следовательно, координаты точки  удовлетворяют уравнению плоскости удовлетворяют уравнению плоскости 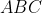 : :
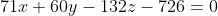
 + 60(6+60t) - 132(-11-132t) - 726 = 0 )
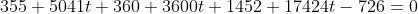
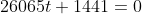

 )
 )
 )
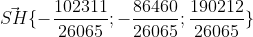

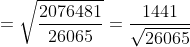
Длина высоты равна 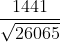
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 5 марта 2010 11:25 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.9.1 Аналитическая геометрия
2.9.1 Аналитическая геометрия

 Форум
Форум

 Математика
Математика

 2.9.1 Аналитическая геометрия
2.9.1 Аналитическая геометрия