irinalavruchina
Новичок
|
     
даны вектора |a|=4 |b|=6 угол между векторами = пи/3 Найти1)cos угла между (a- b)и(2a-3b) 2)площадб параллелограмма построенного на векторах (-a+2b) и (2a+3b)
2задача
Найти вектор а если он перпендикулярен векторам в(1;2;3) и с=2i+j-k и удовлетворяют условию (а*d)=5 где d=(1;1;1)
|
Всего сообщений: 16 | Присоединился: январь 2010 | Отправлено: 8 янв. 2010 9:47 | IP
|
|
Sunny
Новичок
|
 
Пожалуйста, погите с заданием:
Даны вершины треугольника A(1;1) B(2:-3) C(3;4). Составте уравнеие перпендикуляра, опущенного из вершины A на медиану, проведенную из вершины B.
вродебы все просто, но никак не могу сообразить, а заданий еще куча и время поджимает.
Заранее спасибо.
|
Всего сообщений: 1 | Присоединился: январь 2010 | Отправлено: 8 янв. 2010 22:37 | IP
|
|
GarP
Новичок
|
Поясните в чём заключается смысл rot, div b grad в математическом анализе
|
Всего сообщений: 1 | Присоединился: январь 2010 | Отправлено: 24 янв. 2010 18:01 | IP
|
|
uki13
Новичок
|
даны координаты вершин тр-ка АВС.найти длинну стороны АС,уравнение медианы СМ,координаты точки пересечения высот Z. внутренний угол А.сделать чертеж. координаты вершин тр-ка: А(0,1) ; В(6,4); С(3,5)
задача 2:
1 вычислите длину вектора АВ
2 найдите величину скалярного произведения ( АВ,ВС)
3 найти угол между векторами АВ и АС
4 найти вектор АВ-2ВС+3АС
А(0,1) В(6,4) С(3,5)
|
Всего сообщений: 5 | Присоединился: февраль 2010 | Отправлено: 7 фев. 2010 13:06 | IP
|
|
RKI 
Долгожитель
|
Цитата: uki13 написал 7 фев. 2010 13:06
задача 2:
1 вычислите длину вектора АВ
2 найдите величину скалярного произведения ( АВ,ВС)
3 найти угол между векторами АВ и АС
4 найти вектор АВ-2ВС+3АС
А(0,1) В(6,4) С(3,5)
1.
 )
 )
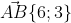
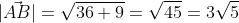
2.
 )
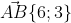
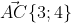
= 6*3+3*4=18+12=30 )
3.
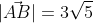
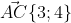
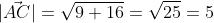
=|\vec{AB}|*|\vec{AC}|*cos(BAC) )
 )
=\frac{30}{15\sqrt{5} } = \frac{2}{\sqrt{5} } )
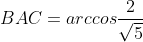
4.
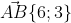
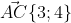
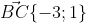
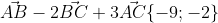
(Сообщение отредактировал RKI 7 фев. 2010 15:07)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 7 фев. 2010 14:47 | IP
|
|
RKI
Долгожитель
|
Цитата: uki13 написал 7 фев. 2010 13:06
даны координаты вершин тр-ка АВС.найти длинну стороны АС,уравнение медианы СМ,координаты точки пересечения высот Z. внутренний угол А.сделать чертеж. координаты вершин тр-ка: А(0,1) ; В(6,4); С(3,5)
длина стороны AC
^{2} + (5-1)^{2} }=\sqrt{9+16}=\sqrt{25}=5 )
-------------------------------------------------------------------
уравнение медианы CM
 )
 )
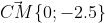
Уравнение медианы CM имеет вид:
|x-3 y-5| = 0
| 0 -2.5|
 - 0 = 0 )
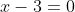
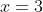
x = 3 - уравнение медианы CM
-------------------------------------------------------------------------------
внутренний угол A
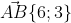
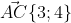
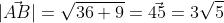
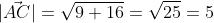
=6*3+3*4=18+12 = 30 )
=|\vec{AB}|*|\vec{AC}|*cosA )
|
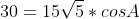
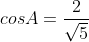
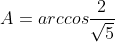
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 7 фев. 2010 15:19 | IP
|
|
RKI
Долгожитель
|
Цитата: uki13 написал 7 фев. 2010 13:06
даны координаты вершин тр-ка АВС.найти длинну стороны АС,уравнение медианы СМ,координаты точки пересечения высот Z. внутренний угол А.сделать чертеж. координаты вершин тр-ка: А(0,1) ; В(6,4); С(3,5)
Точка пересечения высот Z
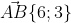
Уравнение прямой AB имеет вид:
|x-0 y-1| = 0
| 6 3|
 = 0 )
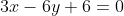
Пусть уравнение высоты CH имеет вид Ax + By + C = 0. Коэффициенты A, B и C небходимо найти.
Прямые AB и CH перпендикулярны. По условию перпендикулярности двух прямых 3A - 6B = 0.
3A = 6B
A = 2B
Уравнение высоты CH принимает вид:
Ax + By + C = 0
2Bx + By + C = 0
Прямая CH проходит через точку C. Следовательно, координаты точки C (3;5) удовлетворяют уравнению прямой CH:
6B + 5B + C = 0
11B + C = 0
C = -11B
Уравнение прямой CH имеет вид:
2Bx + By + C = 0
2Bx + By - 11B = 0 |:B
2x + y - 11 = 0
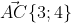
Уравнение прямой AC имеет вид:
|x-0 y-1| = 0
| 3 4|
 = 0 )
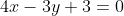
Пусть уравнение высоты BK имеет вид Ax + By + C = 0. Коэффициенты A, B и C небходимо найти.
Прямые AC и BK перпендикулярны. По условию перпендикулярности двух прямых 4A - 3B = 0.
4A = 3B
A = 0.75B
Уравнение высоты BK принимает вид:
Ax + By + C = 0
0.75Bx + By + C = 0
Прямая BK проходит через точку B. Следовательно, координаты точки B (6;4) удовлетворяют уравнению прямой BK:
4.5B + 4B + C = 0
8.5B + C = 0
C = -8.5B
Уравнение прямой BK имеет вид:
0.75Bx + By + C = 0
0.75Bx + By - 8.5B = 0 |:B
0.75x + y - 8.5 = 0
3x + 4y - 34 = 0
Точка Z - точка пересечения высот CH и BK. Для нахождения оординат точки Z необходимо решить систему линейных уравнений:
{2x + y - 11 = 0; 3x + 4y - 34 = 0
{y = - 2x + 11; 3x + 4(-2x+11) - 34 = 0
{y = - 2x + 11; 3x - 8x + 44 - 34 = 0
{y = - 2x + 11; - 5x + 10 = 0
{y = - 2x + 11; x = 2
{x = 2; y = 7
 )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 7 фев. 2010 15:37 | IP
|
|
uki13
Новичок
|
спасибо большое!!!! 
|
Всего сообщений: 5 | Присоединился: февраль 2010 | Отправлено: 7 фев. 2010 16:06 | IP
|
|
TommyKawaii
Новичок
|
1. Найти потенциальную функцию двумя способами, (условия dP/dy=dQ/dx НЕ выполняются вроде... )
a(M)=((x/y)+(3*(e^x)*(z^2))i+((y^2)*z-((x^2)/(2*(y^2)))j+(6*(e^x)*z+(z*(y^3)/3))k
как быть с такой задачей ? сталкивался только с выполняющимися условиями(
2. a(M)=(x+y)i+(y+z)j+(z+x)k
условия : y=2x ; y=4x ; x=1 (замкнутая) нормаль внешняя
z=y^2 ; z=0
посчитал дивергент , получился равным 3
не могу понять что дальше делать с этими всеми условиями и куда их подставлять, как быть с пределами интегрирования и какой у должен получиться график вообще исходя их этих условий ?
(Сообщение отредактировал attention 20 фев. 2010 15:58)
|
Всего сообщений: 17 | Присоединился: февраль 2010 | Отправлено: 19 фев. 2010 18:35 | IP
|
|
attention
Долгожитель
|
TommyKawaii, задание полностью в оригинале запости, тогда возможно будет помочь.
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 19 фев. 2010 23:29 | IP
|
|
|
Форум
2.5.4 Векторная алгебра и векторный анализ
