Genrih
Удален
|
   
Цитата: Guest написал 19 авг. 2006 18:53
izvinite chto tak rastyanulos' pishu vruchnuyu chto vidaet programa
-5/6 1/6 1/6 1/6 1/6 1/6 1/6
1/6 -5/6 1/6 1/6 1/6 1/6 1/6
1/6 1/6 -5/6 1/6 1/6 1/6 1/6
--------- i t.k.d. dumayu princip ponyat
Обратная матрица
стандартно используют формулу для алгебраического дополнения.
В Вaшем случае (симметричная матрица) можно попробовать и методом Гаусса.
|
Всего сообщений: N/A | Присоединился: N/A | Отправлено: 19 авг. 2006 20:20 | IP
|
|
Guest
Новичок
|
спасибо за столь "огромную" помощь
|
Всего сообщений: Нет | Присоединился: Never | Отправлено: 20 авг. 2006 19:25 | IP
|
|
Guest
Новичок
|
Помогите подруге. Плиз
1. Задания по линейной алгебре:
А) Найти определитель матрицы:
0 1 3
А= 2 3 5
3 5 7
Б) Решить систему уравнений методом Крамера:
2х1+х2-х3=0
3х2+4х3=-6
х1+х3=1
|
Всего сообщений: Нет | Присоединился: Never | Отправлено: 13 дек. 2006 13:42 | IP
|
|
Kellog
Начинающий
|
1)
det(A)=0+1*(5*3-2*7)+3*(2*5-3*3)=4
2)
2 1 -1
А= 0 3 4 det(A)=2*3+1*4+1*3=13
1 0 1
det(A) нашли, теперь ищем det(A1), то есть определитель матрицы, составленной из элементов матрицы A, но только первый ее столбец заменяем столбцом свободного члена получакм:
0 1 -1
А1= -6 3 4 det(A1)=0+1*(4*1+6*1)+1*3=13
1 0 1
Затем аналогично det(A2), где
2 0 -1
А2= 0 -6 4 det(A2)=2*(-6*1-4*1)+0-1*6=-26
1 1 1
И соответственно
2 1 0
А3= 0 3 -6 det(A3)=2*3+1*(-6)+0=0
1 0 1
Таким образом ответ:
х1=det(A1)/det(A)=13/13=1
х2=det(A2)/det(A)=-26/13=-2
х3=0
|
Всего сообщений: 79 | Присоединился: ноябрь 2006 | Отправлено: 15 дек. 2006 3:06 | IP
|
|
Stroks
Удален
|
Определитель n-го порядка. Как посчитать правый?
Я пробовал разложить по первой строке и столбцу, в надежде получить какое-либо реккурентное соотношение. Но тогда рушится закономерность в диагоналях, что не приводит ни к чему хорошему.
|
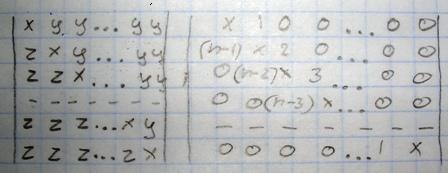
Всего сообщений: N/A | Присоединился: N/A | Отправлено: 19 дек. 2006 18:40 | IP
|
|
ulyannn
Удален
|
Необходимо решить систему уравнений:
x-2y+3z=1
2x-4y+6z=5
4x-8y+12z=-7
По внешнему виду можно сказать,то решений нет.
Все определители равны нулю, а это значит, что решений
бесконечное множество.
Помогите!
|
Всего сообщений: N/A | Присоединился: N/A | Отправлено: 28 дек. 2006 9:51 | IP
|
|
sms
Удален
|
Stroks: могу посчитать определитель слева. Нужен?
ulyannn: ну не все уж равны нулю. Умножьте первое уравнение на 2 и сложите со вторым. Получится противоречие, система несовместна. А значит Вы против Крамера... А только Крамер бывает против Крамера, если Вы смотрите старые фильмы.
|
Всего сообщений: N/A | Присоединился: N/A | Отправлено: 3 янв. 2007 10:44 | IP
|
|
76820999902867
Удален
|
Помогите, кому не трудно.
--------------------------------------------------------------------------------
1.)
Найти:
F∩ D, FỤ D, F/ D, F/ D, F× D, F× D,
Если 1) F=[0;2], D{0,14,6}:
2) F=[1;3) U(5;7], D=[2;6].
2)Представить в тригонометрической форме:
-√2+√2i
3)Вычислить:
(√3+i) ³*³
_________
(1+i) ²*²*²
4)Вычислить:
1 0 8
1 4 6
7 4 8
5)Найти АВ, ВА, (АВ, АВ Если
-3 4 2
В= 1 -5 3
0 1 2
-2 1 -1
А= 1 0 2
4 -1 3
б)Вычислить определитель
1 -1 0 3
3 2 1 -1
1 2 -1 3
4 0 1 2
|
Всего сообщений: N/A | Присоединился: N/A | Отправлено: 6 марта 2007 7:28 | IP
|
|
Guest
Новичок
|
Ребята, помогите! Ничего не помню, а тут начальница попросила....
-Х^3-3Х^2+18х-80=0
хоть намекните....
|
Всего сообщений: Нет | Присоединился: Never | Отправлено: 13 марта 2007 13:58 | IP
|
|
Guest
Новичок
|
я эту матрицу никогда не решу!
|
Всего сообщений: Нет | Присоединился: Never | Отправлено: 13 марта 2007 14:04 | IP
|
|
Форум
Матрицы, определители (детерминанты), линейные системы
