Форум - 2.5.4 Векторная алгебра и векторный анализ [8]

Форум	» Назад на решение задач по физике и термеху
Регистрация \| Профиль \| Войти \| Забытый пароль \| Присутствующие \| Справка \| Поиск

» Добро пожаловать, Гость: Войти | Регистрация

	Форум Математика 2.5.4 Векторная алгебра и векторный анализ
	Отметить все сообщения как прочитанные [ Помощь ] » Добро пожаловать на форум "Математика" «

Переход к теме
<< Назад Вперед >>

Несколько страниц [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 ]
Модераторы: Roman Osipov, RKI, attention, paradise

Karim

Начинающий
Вот такие же числа и у меня получились у точки, но они меня смутили. Спасибо еще раз!

Всего сообщений: 86 | Присоединился: октябрь 2009 | Отправлено: 9 нояб. 2009 10:58 | IP

ne umnay

Новичок
Помогите пожалуйста.
Нужно найти расстояние от точки (1;1) до прямой x=2y+1
Только обязательно через алгебру, через линейные многообразие.

(Сообщение отредактировал ne umnay 17 нояб. 2009 0:44)

Всего сообщений: 3 | Присоединился: ноябрь 2009 | Отправлено: 17 нояб. 2009 0:43 | IP

Lesechka

Новичок
Здравствуйте....
Координаты вершин пирамиды А1(-4, 8, -1) А2(5, -1, 6) А3(6, -1, 8) А4(0, -4, 2)
найти
1)угол между ребрами А1А2 и А1А4
2)угол между ребром А1А4 и гранью А1А2А3
3)площадь грани А1А2А3
4) объем пирамиды
5)уравнение высоты на А1А2А3
6) координаты основания этой высоты

пожалуйста, помогите.....
ответы какие-то странные получаются(

Всего сообщений: 6 | Присоединился: ноябрь 2009 | Отправлено: 18 нояб. 2009 2:31 | IP

RKI

Долгожитель

Цитата: Lesechka написал 18 нояб. 2009 2:31

Координаты вершин пирамиды А1(-4, 8, -1) А2(5, -1, 6) А3(6, -1, 8) А4(0, -4, 2)
найти
1)угол между ребрами А1А2 и А1А4

$A_{1} (-4, 8, -1)$
$A_{2} (5, -1, 6)$
$A_{4} (0, -4, 2)$

$\vec{A_{1}A_{2} } \{ 9, -9, 7 \}$
$\vec{A_{1}A_{4} } \{ 4, -12, 3 \}$

$|\vec{A_{1}A_{2} }| = \sqrt{81 + 81 + 49} = \sqrt{211}$
$|\vec{A_{1}A_{4} }| = \sqrt{16 + 144 + 9} = \sqrt{169} = 13$

$(\vec{A_{1}A_{2} }; \vec{A_{1}A_{4} }) = 9*4 + (-9)*(-12) + 7*3 = 36 + 108 + 21 = 165$

$(\vec{A_{1}A_{2} }; \vec{A_{1}A_{4} }) = |\vec{A_{1}A_{2} }|*|\vec{A_{1}A_{4} }|*cosA_{2}A_{1}A_{4} =$

$= 13\sqrt{211}*cosA_{2}A_{1}A_{4} = 165$

$cosA_{2}A_{1}A_{4} = \frac{165}{13\sqrt{211} }$

$A_{2}A_{1}A_{4} = arccos\frac{165}{13\sqrt{211} }$

Цитата: Lesechka написал 18 нояб. 2009 2:31

Координаты вершин пирамиды А1(-4, 8, -1) А2(5, -1, 6) А3(6, -1, 8) А4(0, -4, 2)
2)угол между ребром А1А4 и гранью А1А2А3

$A_{1} (-4, 8, -1)$
$A_{4} (0, -4, 2)$

$\vec{A_{1}A_{4} } \{ 4, -12, 3 \}$

Уравнение прямой A1A4 имеет вид:
$\frac{x+4}{4} = \frac{y-8}{-12} = \frac{z+1}{3}$

$l = 4$
$m = -12$
$n = 3$

$A_{1} (-4, 8, -1)$
$A_{2} (5, -1, 6)$
$A_{3} (6, -1, 8)$

$\vec{A_{1}A_{2} } \{ 9, -9, 7 \}$
$\vec{A_{1}A_{3} } \{ 10, -9, 9 \}$

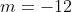
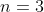
Уравнение плоскости A1A2A3 имеет вид:
|x+4 y-8 z+1| = 0
| 9 -9 7|
| 10 -9 9|

(x+4)*|-9 7| - (y-8)*|9 7| + (z+1)*|9 -9| = 0
|-9 9| |10 9| |10 -9|

(x+4)*(-81+63) - (y-8)*(81-70) + (z+1)*(-81+90) = 0

- 18(x+4) - 11(y-8) + 9(z+1) = 0

- 18x - 72 - 11y + 88 + 9z + 9 = 0

- 18x - 11y + 9z + 25 = 0

18x + 11y - 9z - 25 = 0

$a = 18$
$b = 11$
$c = - 9$

$\phi$ - угол между ребром A1A4 и плоскостью A1A2A3

$sin\phi = \frac{|al + bm + cn|}{\sqrt{a^{2} + b^{2} + c^{2} }\sqrt{l^{2} + m^{2} + n^{2} } } =$

$= \frac{|72 - 132 - 27|}{\sqrt{324 + 121 + 81}\sqrt{16 + 144 + 9} } = \frac{87}{13\sqrt{526} }$

$\phi = arcsin\frac{87}{13\sqrt{526} }$

Цитата: Lesechka написал 18 нояб. 2009 2:31

Координаты вершин пирамиды А1(-4, 8, -1) А2(5, -1, 6) А3(6, -1, 8) А4(0, -4, 2)
3)площадь грани А1А2А3

$\vec{A_{1}A_{2} } \{ 9, -9, 7 \}$
$\vec{A_{1}A_{3} } \{ 10, -9, 9 \}$

$\vec{A_{1}A_{2} } \times \vec{A_{1}A_{3} } =$

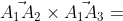
= | i j k| = i*|-9 7| - j*| 9 7| + k*| 9 -9| =
| 9 -9 7| |-9 9| |10 9| |10 -9|
|10 -9 9|

= i*(-81+63) - j*(81 - 70) + k*(-81 + 90) = - 18i - 11j + 9k

$\vec{A_{1}A_{2} } \times \vec{A_{1}A_{3} } \{ -18, -11, 9 \}$

$|\vec{A_{1}A_{2} } \times \vec{A_{1}A_{3} }| = \sqrt{324 + 121 + 81} = \sqrt{526}$

$S_{A_{1}A_{2}A_{3} } = \frac{|\vec{A_{1}A_{2} } \times \vec{A_{1}A_{3} }|}{2} = \frac{\sqrt{526} }{2}$

Цитата: Lesechka написал 18 нояб. 2009 2:31

Координаты вершин пирамиды А1(-4, 8, -1) А2(5, -1, 6) А3(6, -1, 8) А4(0, -4, 2)
4) объем пирамиды

$A_{1} (-4, 8, -1)$
$A_{2} (5, -1, 6)$
$A_{3} (6, -1, 8)$
$A_{4} (0, -4, 2)$

$\vec{A_{4}A_{1} } \{ -4, 12, -3 \}$
$\vec{A_{4}A_{2} } \{ 5, 3, 4 \}$
$\vec{A_{4}A_{3} } \{ 6, 3, 6 \}$

$(\vec{A_{4}A_{1} }; \vec{A_{4}A_{2} }; \vec{A_{4}A_{3} }) =$

= |-4 12 -3| = -4*|3 4| - 12*|5 4| - 3*|5 3| =
| 5 3 4| |3 6| |6 6| |6 3|
| 6 3 6|

= -4*(18 - 12) - 12*(30 - 24) - 3*(15 - 18) =
= - 24 - 72 + 9 = - 87

$V_{A_{1}A_{2}A_{3}A_{4} } = \frac{|(\vec{A_{4}A_{1} }; \vec{A_{4}A_{2} }; \vec{A_{4}A_{3} })|}{6} = \frac{87}{6} = \frac{29}{2}$

Цитата: Lesechka написал 18 нояб. 2009 2:31

Координаты вершин пирамиды А1(-4, 8, -1) А2(5, -1, 6) А3(6, -1, 8) А4(0, -4, 2)
5)уравнение высоты на А1А2А3

$A_{4} (0, -4, 2)$

Уравнение высоты A4H имеет вид:
$\frac{x}{l} = \frac{y+4}{m} = \frac{z-2}{n}$

Коэффициенты l, m и n необходимо найти.

Уравнение плоскости A1A2A3 имеет вид:
$18x + 11y - 9z - 25 = 0$

По условию перпендикулярности прямой и плоскости в пространстве
$\frac{l}{18} = \frac{m}{11} = \frac{n}{-9}$

$l = -2n \ \ \ m = - \frac{11n}{9}$

Уравнение высоты A4H имеет вид:
$\frac{x}{-2n} = \frac{y+4}{-\frac{11n}{9} } = \frac{z-2}{n}$

$\frac{x}{-2} = \frac{y+4}{-\frac{11}{9} } = z-2$

Цитата: Lesechka написал 18 нояб. 2009 2:31
Здравствуйте....
Координаты вершин пирамиды А1(-4, 8, -1) А2(5, -1, 6) А3(6, -1, 8) А4(0, -4, 2)
6) координаты основания этой высоты

H (x,y,z)

Точка H лежит на прямой A4H. Следовательно, координаты точки H удовлетворяют уравнению прямой A4H:

$\frac{x}{-2} = \frac{y+4}{-\frac{11}{9} } = z-2 = t$

$x = -2t \ \ \ y = - 4 - \frac{11t}{9} \ \ \ z = 2+t$

H (-2t; -4-11t/9; 2+t)

Точка H лежит на плоскости A1A2A3. Следовательно, координаты точки H удовлетворяют уравнению плоскости A1A2A3:

$18x + 11y - 9z - 25 = 0$

$-36t - 44 - \frac{121t}{9} - 18 - 9t - 25 = 0$

$- \frac{526t}{9} - 87 = 0$

$t = - \frac{783}{526}$

$H (\frac{783}{263}; -\frac{1147}{526}; \frac{269}{526})$

(Сообщение отредактировал attention 9 дек. 2009 6:44)

Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 18 нояб. 2009 13:56 | IP

Lesechka

Новичок
Нужно найти координаты конца вектора с, если начало вектора находится в точке М0(нулевое)...
с=(1, -2, 5)
М0 = (4, -1, 2)

Всего сообщений: 6 | Присоединился: ноябрь 2009 | Отправлено: 18 нояб. 2009 19:07 | IP

fler

Новичок
Дана система векторов a1;a2;a3;a4;a5;a6 в которой a3 = (0,1,1,2), a4=(1,1,1,3)a5=(1,0,-2,-1)a6=(1,0,1,2). Дополнить линейно независимую часть а1=(5,2,7,14), а2=(2,11,-10,3) до базиса системы векторов a1;a2;a3;a4;a5 и все векторы, не вошедшие в базис, разложить по базису.

Всего сообщений: 1 | Присоединился: ноябрь 2009 | Отправлено: 22 нояб. 2009 8:08 | IP

mDv

Новичок
1) Определить собственные значения и собственные векторы матрицы:
A =
-13 3
-14 11

2) Привести квадратичную форму к каноническому виду:

2x2+5y2+11z2-20xy+4zx-16yz.

двойки после букв ето квадрат

Всего сообщений: 1 | Присоединился: ноябрь 2009 | Отправлено: 24 нояб. 2009 14:59 | IP

blendas

Новичок
Здравствуйте, помогите, пожалуйста!

Найдите косинус угла между векторами: |а|=4, |b|=3, аb = 6.

СПАСИБО!

(Сообщение отредактировал attention 9 дек. 2009 5:54)

Всего сообщений: 10 | Присоединился: октябрь 2009 | Отправлено: 3 дек. 2009 12:15 | IP

STRELLA

Новичок
Помогите кто может!!!

Зараннее огромное спасибо.

Вычислить поток векторного поля:a=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k через внешнюю поверхность пирамиды, образуемую плоскостью Р и координатными плоскостями, двумя способами:

а) использовав определение потока;
б) с помощью формулы Остроградского-Гаусса.

(Сообщение отредактировал attention 8 дек. 2009 18:14)

(Сообщение отредактировал STRELLA 10 дек. 2009 18:10)

Всего сообщений: 17 | Присоединился: ноябрь 2009 | Отправлено: 8 дек. 2009 18:47 | IP

Amalfy

Новичок
Здравствуйте, помогите решить задачку - нигде не нашла подобной, чтобы разобраться самой...
Векторы а и b составляют угол 45. Найти площадь треугольника, построенного на веторах a-2b и 3a+2b, если |a|=|b|=5. Заранее спасибо.

Всего сообщений: 5 | Присоединился: декабрь 2009 | Отправлено: 8 дек. 2009 22:56 | IP

Отправка ответа:

Имя пользователя Вы зарегистрировались?
Пароль Забыли пароль?
Сообщение
Использование HTML запрещено
Использование IkonCode разрешено
Смайлики разрешены

Опции отправки
Добавить подпись?
Получать ответы по e-mail?
Разрешить смайлики в этом сообщении?
Просмотреть сообщение перед отправкой? Да Нет

Переход к теме
<< Назад Вперед >> Несколько страниц [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 ]