Karim


Начинающий
|
      
Огромное спасибо!
Помогите пожалуйста еще с одним заданием
данный участок имеет четырехугольную форму. В вершинах вбиты 4 столба А, В, С, D.
Нужно найти координаты столба D, если известно что он расположен симметрично столбу А относительно прямой ВС.
А(4, 13)
В(-6, 8)
С(6, -1)
Проверьте пожалуйста, я тут что то пытался сделать:
находим уравнение прямой ВС
(у-8)/-9=(х+6)/12, =>
3х+4у-14=0
(х-4)/3=(у-13)/4,
4х-3у+23=0.
Решаем систему двух уравнений
{4х-3у+23=0
{3х+4y-14=0
х=-2
y=5.
D(-2, 5).
Правильно?
(Сообщение отредактировал attention 9 дек. 2009 6:35)
|
Всего сообщений: 86 | Присоединился: октябрь 2009 | Отправлено: 29 окт. 2009 20:57 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Karim написал 31 окт. 2009 21:39
данный участок имеет четырехугольную форму. В вершинах вбиты 4 столба А, В, С, D.
Нужно найти координаты столба D, если известно что он расположен симметрично столбу А относительно прямой ВС.
А(4, 13)
В(-6, 8)
С(6, -1)
 )
 )
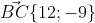
Уравнение стороны BC имеет вид:
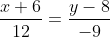
 = -4(y-8) )
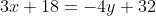
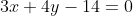
Постороим перпендикуляр h к прямой BC, проходящий через точку A.
Пусть уравнение перпендикуляра h имеет вид: ax + by + c = 0. Коэффициенты a, b и c необходимо найти.
Прямые h: ax + by + c = 0 и BC: 3x + 4y - 14 = 0 перпендикулярны. По условию перпендикулярности двух прямых на плоскости
3a + 4b = 0
4b = - 3a
Уравнение прямой h принимает вид:
ax + by + c = 0
4ax + 4by + 4c = 0
4ax - 3ay + 4c = 0
Прямай h проходит через точку A (4; 13). Следовательно, координаты точки A удовлетворяют уравнению прямой h:
4a*4 - 3a*13 + 4c = 0
16a - 39a + 4c = 0
- 23a + 4c = 0
4c = 23a
Таким образом, уравнение перпендикуляра h имеет вид:
4ax - 3ay + 4c = 0
4ax - 3ay + 23a = 0
4x - 3y + 23 = 0
Найдем точку пересечения прямой BC и перпендикуляра h. Для этого необходимо решить систему динейных уравнений:
3x + 4y - 14 = 0; 4x - 3y + 23 = 0
x = - 2; y = 5
H(-2; 5)
Искомая точка D лежит на перпендикуляре h и AH = HD.
D(x; y)
Точка D(x;y) лежит на прямой h: 4x - 3y + 23 = 0. Следовательно, координаты точки D удовлетворяют уравнению прямой h:
4x - 3y + 23 = 0
4x = 3y - 23
x = (0.75)y - 5.75
D ((0.75)y - 5.75; y)
 )
 )
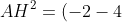^{2} + (5-13)^{2} = 36 + 64 = 100 )
 )
 )
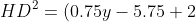^{2} + (y-5)^{2} = (0.75y - 3.75)^{2} + (y-5)^{2} = )
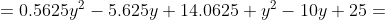
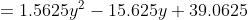
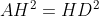
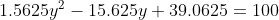
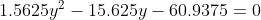
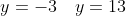
Значение y = 13 соотвествует точке A, а y = - 3 - точке D
D ((0.75)y - 5.75; y)
D (-8; -3)
(Сообщение отредактировал RKI 1 нояб. 2009 13:08)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 1 нояб. 2009 13:07 | IP
|
|
Karim


Начинающий
|
      
Ого, тут столько писанины, а я попытался сделать в две строчки! Огромное спасибо, RKI, ТЫ-КРАСАВЧИК! Спасибо
|
Всего сообщений: 86 | Присоединился: октябрь 2009 | Отправлено: 1 нояб. 2009 13:15 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Karim написал 1 нояб. 2009 13:15
Ого, тут столько писанины, а я попытался сделать в две строчки! Огромное спасибо, RKI, ТЫ-КРАСАВЧИК! Спасибо
Пожалуйста.
Только я - это она 
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 1 нояб. 2009 13:24 | IP
|
|
Karim


Начинающий
|
      
Ой, извини!
Тогда ты просто КРАСОТКА! :-)
|
Всего сообщений: 86 | Присоединился: октябрь 2009 | Отправлено: 1 нояб. 2009 13:55 | IP
|
|
jaredleto


Новичок
|
     
1)
а - постоянный вектор поля
r=x*i+y*j+z*k r=|r|
Найти divF, rotF если F = [a,r]
F - векторное поле
2)
Найти циркуляцию векторного поля F вдоль кривой гамма, пробегаемой один раз в положительном направлении, если смотреть из начала координат
F=(y^2)*z*i+(y^2)j+(z^2)k
если кривая гамма задана так:
z^2 = 2 - x^2; x^2 - y^2 - + z^2 =1 (y>0)
3)
Найти поток веторного поля F каждый гладкий кусок границы области D в направлении внешней нормали:
F = x*z*i + y*z*j + (z^2 -1 )*k
D: sqrt(x^2 + y^2)<z<4
4)
Найти поток векторного поля F через границу области ограниченной указанными поверхностями, в направлении внешней нормали
F = (2x+y)*i + (y+2x)*j + (x+y)*k
S1: 4*(x^2 + y^2) = z
S2: 4*x^2 + 4*y^2 + z =2
5)
Найти работу векторного поля F при перемещении вдоль кривой гамма от точки А к точке В :
F = x*i + (x+y+z)*j + y*k
гамма задана так:
x = sin(z); x+y+z = 1
A(0;1;0)
B(1; -pi/2; pi/2)
6)
Найти векторные линии данного векторного поля F:
F = 2x*i + 4y*j
7)
Вычислить интеграл скалярного поля f по поверхности S:
f=sqrt(x^2 + z^2)
S: (x^2)/9 + (z^2)/9 - (y^2)/16 = 0 , 0<=y<=4
|
Всего сообщений: 2 | Присоединился: ноябрь 2009 | Отправлено: 4 нояб. 2009 22:17 | IP
|
|
jaredleto


Новичок
|
     
может кто-то знает как делать какое-то из заданий)?
помогите пожалуйста =)
|
Всего сообщений: 2 | Присоединился: ноябрь 2009 | Отправлено: 8 нояб. 2009 10:55 | IP
|
|
ProstoVasya

Долгожитель
|
     
4. Для вычисления потока векторного поля сквозь замкнутую поверхность используем формулу Остроградского-Гаусса. При вычислении интеграла по объёму используем цилиндрические координаты

|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 8 нояб. 2009 12:12 | IP
|
|
Karim


Начинающий
|
      
Здравствуйте еще раз, помогите пожалуйста мне разобраться, запутался.
задача.
Треугольник задан вершинами
А(-2;-2), В(7;-6), С(1;2). Нужно написать уравнение окружности с центром в А, для которой ВС служит касательной.
решение.
Так как ВС- касательная к окружности, то радиус данной окружности перпендикулярен касательной.
Найдем уравнение прямой ВС:
(у+6)/(2+6)=(х-7)/(1-7)......
у=-4/3 х+10/3.
Найдем уравнение прямой АЕ, перпендикулярной прямой ВС. По свойству перпендикулярности k1=-1/k2. Тогда прямая АЕ будет иметь вид у=3/4 х+b. Подставив точку А в это уравнение получаем, что
АЕ: у=3/4 х-1/2.
Так как АЕ-радиус, то нам необходимо найти длину отрезка АЕ, для этого находим координату точки Е, решив систему уравнени
{у=3/4 х-1/2,
{у=-4/3 х+10/3.
И вот дальше получается полный бред! Где я ошибся?
(Сообщение отредактировал Karim 9 нояб. 2009 0:46)
|
Всего сообщений: 86 | Присоединился: октябрь 2009 | Отправлено: 9 нояб. 2009 0:43 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Karim написал 9 нояб. 2009 0:43
задача.
Треугольник задан вершинами
А(-2;-2), В(7;-6), С(1;2). Нужно написать уравнение окружности с центром в А, для которой ВС служит касательной.
 )
 )
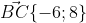
Уравнение прямой BC имеет вид:
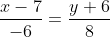
 = -3(y+6) )
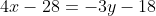
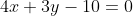
Построим перпендикуляр AH к прямой BC, где точка H - пересечение прямых AH и BC.
Пусть прямая AH имеет своим уравнением следующее равенство: ax + by + c = 0. Коэффициенты a, b и c необходимо определить.
Прямая AH: ax + by + c = 0 и BC: 4x + 3y - 10 = 0 перпендикулярны. По условию перпендикулярности двух прямых в плоскости
4a + 3b = 0
3b = - 4a
Уравнение прямой AH принимает вид:
ax + by + c = 0
3ax + 3by + 3c = 0
3ax - 4ay + 3c = 0
Точка A (-2;-2) лежит на прямой AH. Следовательно, координаты точки A удовлетворяют уравнению перпендикуляра AH:
3a*(-2) - 4a*(-2) + 3c = 0
- 6a + 8a + 3c = 0
2a + 3c = 0
3c = - 2a
Уравнение перпендикуляра AH имеет вид:
3ax - 4ay + 3c = 0
3ax - 4ay - 2a = 0
3x - 4y - 2 = 0
Точка H является точкой пересечения прямых BC и AH. Поэтому для нахождения координат точки H необходимо решить систему уравнений:
{4x + 3y - 10 = 0; 3x - 4y - 2 = 0
{x = 46/25; y = 22/25
H (46/25; 22/25)
A (-2; -2)
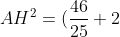^{2} + (\frac{22}{25} + 2)^{2} = \frac{9216}{625} + \frac{5184}{625} = \frac{576}{25} )
Запишем уравнение окружности с центом в точке A(-2;-2) и радиусом AH:
^{2} + (y+2)^{2} = \frac{576}{25} )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 9 нояб. 2009 8:36 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 2.5.4 Векторная алгебра и векторный анализ
2.5.4 Векторная алгебра и векторный анализ

 Форум
Форум

 Математика
Математика

 2.5.4 Векторная алгебра и векторный анализ
2.5.4 Векторная алгебра и векторный анализ