MEHT
Долгожитель
|
    
Ну тогда понятно) Просто решили "устрашить" поле функциями, фактически не влияющими на вычисление дивергенции.
Можно выбросить из поля этот самый логарифм, который всё портит, или же заменить его другой функцией z, существущей на заданной сфере - условия теоремы будут выполнены и ответ сойдётся.
(Сообщение отредактировал MEHT 5 апр. 2012 19:25)
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 5 апр. 2012 19:24 | IP
|
|
Dim
Новичок
|
Возможно)
А подскажите, если заменить, как Вы говорите-то как у меня получится в этом случае:
Найти поток векторного поля a через замкнутую поверхность S (нормаль внешняя)
a=(lny+7*x)*i+(sinz-2*y)*j+(e^y-2*z)/4)*k
S: x^2+y^2+z^2=2*x+2*y+2*z-2
|
Всего сообщений: 42 | Присоединился: январь 2012 | Отправлено: 5 апр. 2012 19:27 | IP
|
|
MEHT
Долгожитель
|
S это (x-1)^2 + (y-1)^2 + (z-1)^2 = 1 - сфера радиуса 1 с центром в точке (1,1,1)
Тут всё благополучно с полем, за исключением одной точки сферы (1,0,1) - в этой точке вектор a неопределён.
Если выбросить этот не влияющий на вычисление дивергенции логарифм, правый интеграл в формуле Остроградского вычисляется аналогично предыдущему.
Тут дивергенция
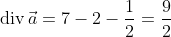
а объём для шара радиуса 1.
Окончательное перемножение оъбёма (4/3) п на 9/2 даст 6п.
(Сообщение отредактировал MEHT 5 апр. 2012 19:51)
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 5 апр. 2012 19:41 | IP
|
|
Dim
Новичок
|
А разве дивергенция в данном случае не такая: div a=7-2-2=3?
То есть поток будет равен:
3* 3/4* П*R^3 = 4П ?
|
Всего сообщений: 42 | Присоединился: январь 2012 | Отправлено: 5 апр. 2012 19:45 | IP
|
|
MEHT
Долгожитель
|
Нет, в z-компоненте поля ещё деление на четвёрку.
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 5 апр. 2012 19:50 | IP
|
|
Dim
Новичок
|
Извините, опечатка-вот так должно быть:
a=(lny+7*x)*i+(sinz-2*y)*j+(e^y-2*z)*k
S: x^2+y^2+z^2=2*x+2*y+2*z-2
|
Всего сообщений: 42 | Присоединился: январь 2012 | Отправлено: 5 апр. 2012 19:55 | IP
|
|
MEHT
Долгожитель
|
Да, тогда 4п.
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 5 апр. 2012 19:59 | IP
|
|
Dim
Новичок
|
Хорошо) Спасибо большое за помощь)
|
Всего сообщений: 42 | Присоединился: январь 2012 | Отправлено: 5 апр. 2012 20:00 | IP
|
|
MEHT
Долгожитель
|
;)
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 5 апр. 2012 20:01 | IP
|
|
Vasilisk
Новичок
|
Помогите пожалуйста решить
при каких n векторы а=(n;3;2) и b=(-2;n;7) перпендикулярны?
|
Всего сообщений: 7 | Присоединился: май 2012 | Отправлено: 25 мая 2012 13:53 | IP
|
|
Форум
2.5.4 Векторная алгебра и векторный анализ
