Dim

Новичок
|
     
Помогите, пожалуйста, решить: Найти поток a векторного поля через замкнутую поверхность (нормаль внешняя)
a=(4*x-2*y^2)*i+(lnz-4*y)*j+(x+(3*z)/4)*k
S: x^2+y^2+z^2=2*x+3
Кто поможет--буду очень рада. Спасибо)
|
Всего сообщений: 42 | Присоединился: январь 2012 | Отправлено: 2 апр. 2012 21:00 | IP
|
|
Dim

Новичок
|
     
Я пробовала, но не всё могу решить.
|
Всего сообщений: 42 | Присоединился: январь 2012 | Отправлено: 2 апр. 2012 21:01 | IP
|
|
MEHT


Долгожитель
|
     
Кстати, не сразу обратил внимание - ваше поле не определено для отрицательных или равного нулю z (из-за логарифма в y-компоненте поля). Тем самым через нижнюю половину заданной сферы S поток неопределён.
Таким образом, не прибегая к вычислениям можно говорить, что поток неопределён (несуществует).
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 3 апр. 2012 1:44 | IP
|
|
Dim

Новичок
|
     
А какие-нибкдь доказательства есть?----что поток не существует
|
Всего сообщений: 42 | Присоединился: январь 2012 | Отправлено: 4 апр. 2012 0:24 | IP
|
|
Dim

Новичок
|
     
Помогите, пожалуйста с таким заданием:
Найти поток векторного поля a через замкнутую поверхность S (нормаль внешняя)
a=(lny+7*x)*i+(sinz-2*y)*j+(e^y-2*z)/4)*k
S: x^2+y^2+z^2=2*x+2*y+2*z-2
|
Всего сообщений: 42 | Присоединился: январь 2012 | Отправлено: 4 апр. 2012 0:27 | IP
|
|
MEHT


Долгожитель
|
     
Цитата: Dim написал 4 апр. 2012 0:24
А какие-нибкдь доказательства есть?----что поток не существует
Это очевидно 
Посмотрите как задан вектор a - в него входит ln(z). Логарифм определён лишь для положительных z,
А сфера S, через которую должен вычислятся поток этого самого вектора, частью своей поверхности вылезла в область отрицательных z.
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 4 апр. 2012 18:25 | IP
|
|
Dim

Новичок
|
     
А в ответе написано что равно 8Pi
|
Всего сообщений: 42 | Присоединился: январь 2012 | Отправлено: 5 апр. 2012 12:28 | IP
|
|
MEHT


Долгожитель
|
     
Это неверно. Хотя нетрудно догадаться как получен этот результат.
Взяли формулу Остроградского
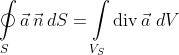
и вычислили интеграл справа:
дивергенция даст постоянную 3/4, которую можно вынести за знак интеграла, оставшийся интеграл представляет собой объём шара, по которому интегрируют. Этот интеграл можно взять перейдя к сферич. координатам. А можно проще - вспомнить что объём шара радиуса r есть
V = (4/3) п r^3; для нашего шара радиус равен 2 (из заданного уравнения сферы).
Окончательно находится, что интеграл справа равен 8п.
Но помимо основной формулы следует также помнить и об условиях теоремы Остроградского. Эти условия несоблюдаются - не существует интеграл слева.
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 5 апр. 2012 18:44 | IP
|
|
MEHT


Долгожитель
|
     
Скажите, а из какого задачника такая расчётка? Если не секрет 
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 5 апр. 2012 18:45 | IP
|
|
Dim

Новичок
|
     
Задачника нет - просто дали задачу и ответ)
|
Всего сообщений: 42 | Присоединился: январь 2012 | Отправлено: 5 апр. 2012 19:18 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.5.4 Векторная алгебра и векторный анализ
2.5.4 Векторная алгебра и векторный анализ

 Форум
Форум

 Математика
Математика

 2.5.4 Векторная алгебра и векторный анализ
2.5.4 Векторная алгебра и векторный анализ