VAsiaaa

Новичок
|
     
Цитата: Cemen написал 26 апр. 2012
Первую задачу, если не ошибаюсь можно решить так : С=25!/(4!*(25-4)! =12650
Вторая задача - количество карт, подходящих под условие, разделить на 36
(Сообщение отредактировал VAsiaaa 27 апр. 2012 9:19)
|
Всего сообщений: 2 | Присоединился: апрель 2012 | Отправлено: 27 апр. 2012 9:16 | IP
|
|
Cemen


Новичок
|
    
спасибо)))
|
Всего сообщений: 2 | Присоединился: апрель 2012 | Отправлено: 27 апр. 2012 18:02 | IP
|
|
Nextos9

Новичок
|
    
Приветствую всех!
Помогите пожалуйста мне найти дисперсию, она у меня всегда получается отрицательной, вроде все верно решаю а всеровно одно и тоже - дисперсия отрицательная.
Вот мое решение внешняя ссылка удалена внешняя ссылка удалена (извеняюсь за сторонний сайт)
Очень прошу о помощи, я три дня с ним возился и ничего не смог не найти в нете, не решить. :-(
(Сообщение отредактировал Nextos9 29 апр. 2012 18:14)
|
Всего сообщений: 4 | Присоединился: апрель 2012 | Отправлено: 29 апр. 2012 16:09 | IP
|
|
ustam


Долгожитель
|
     
Цитата: Nextos9 написал 29 апр. 2012 16:09
Очень прошу о помощи, я три дня с ним возился и ничего не смог не найти в нете, не решить. :-(
За свои мучения скажите "Спасибо" составителю задач. Элементарная опечатка!!!
У вас же не выполняется условие: интеграл в пределах от -бесконечности до +бесконечности от плотности вероятности должно равняться 1, а у вас получается 16!!!
Правильное условие: f(x) = x/8 при 0<x<или равно 4
(Сообщение отредактировал ustam 29 апр. 2012 22:34)
|
Всего сообщений: 420 | Присоединился: декабрь 2008 | Отправлено: 29 апр. 2012 22:29 | IP
|
|
Nextos9

Новичок
|
    
ustam, Спасибо! Действительно на интервале от 0 до 4 все идеально получается.
Тоесть в функции плотности просто была опечатка?
Спасибо еще раз! :-)
|
Всего сообщений: 4 | Присоединился: апрель 2012 | Отправлено: 30 апр. 2012 13:03 | IP
|
|
Nextos9

Новичок
|
    
ustam, У меня теперь еще один вопрос, еще в одном форуме мне ответили что просто нужно найти нормированую функцию и для этого просто разделить текущую функцию плотности на 16, я теперь не пойму где правельный ответ, в примере по котором я делал это задание о нормированой функции и слова небыло. :-(
|
Всего сообщений: 4 | Присоединился: апрель 2012 | Отправлено: 30 апр. 2012 13:54 | IP
|
|
ustam


Долгожитель
|
     
Цитата: Nextos9 написал 30 апр. 2012 13:54
ustam, У меня теперь еще один вопрос, еще в одном форуме мне ответили что просто нужно найти нормированую функцию и для этого просто разделить текущую функцию плотности на 16, я теперь не пойму где правельный ответ, в примере по котором я делал это задание о нормированой функции и слова небыло. :-(
У вас обычная задача, к нормированию отношения не имеет. Просто элементарная опечатка.
|
Всего сообщений: 420 | Присоединился: декабрь 2008 | Отправлено: 30 апр. 2012 14:15 | IP
|
|
Nextos9

Новичок
|
    
ustam, Спасибо еще раз! А то я уже был в непонятке.
|
Всего сообщений: 4 | Присоединился: апрель 2012 | Отправлено: 30 апр. 2012 14:17 | IP
|
|
vin0gradof


Новичок
|
    
Здравствуйте! Прошу помощи со следующей задачей:
Для подготовки к экзамену студенту необходимо подготовить 2n вопросов. Каждый билет содержит 2 вопроса. Комплектация билетов вопросами осуществляется случаынйм образом. Студент подготовил r вопросов. Найти вероятность того, что он сдаст экзамен, если для этого необходимо ответить на два вопроса своего билета или на один вопрос своего билета и один доволнительный вопрос по выбору преподавателя.
Все остальное решил, эту не могу. Теорвер все-таки последний раз был лет 6-7 назад
|
Всего сообщений: 3 | Присоединился: апрель 2012 | Отправлено: 30 апр. 2012 18:33 | IP
|
|
MEHT


Долгожитель
|
    
Укомплектовать 2n вопросов в билеты по два вопроса каждый можно 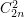 способами. (При таком подсчёте билеты структуры {вопрос1, вопрос2} тождественны билетам {вопрос2, вопрос1}. Это надо уяснить, дабы не было впоследствии недоразумений при подсчёте). способами. (При таком подсчёте билеты структуры {вопрос1, вопрос2} тождественны билетам {вопрос2, вопрос1}. Это надо уяснить, дабы не было впоследствии недоразумений при подсчёте).
Количество "полностью удачных" билетов укомплектовывались бы по такому же принципу и составлялись из r выученных вопросов, т.е. всего их будет 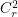 штук в этой общей нашей кучке из штук в этой общей нашей кучке из 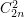 . .
Теперь подсчитаем количество "на половину удачных" билетов. Они будут комплектоваться таким способом, что один из вопросов в них - из выученых, второй - из оставшихся невыученых: 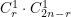 . Если будет иметь место такой "полусчастливый" билет, то придётся ещё отвечать на 1 доп.вопрос, который будет случайно выбран из общей кучки 2n вопросов. А, как мы знаем, из них только r вопросов благоприятны для успешной сдачи экзамена. . Если будет иметь место такой "полусчастливый" билет, то придётся ещё отвечать на 1 доп.вопрос, который будет случайно выбран из общей кучки 2n вопросов. А, как мы знаем, из них только r вопросов благоприятны для успешной сдачи экзамена.
Вся комбинаторика "благоприятных" и общего количества возможных исходов налицо, можно составлять вероятности по классическому принципу "отношение благоприятного количества исходов к общему количеству":
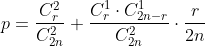
Если ничего не напутал, ответ такой. Осталось только пораскрывать биномиальные коэффициенты.
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 1 мая 2012 17:35 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.6.1(3) Теория вероятности
2.6.1(3) Теория вероятности

 Форум
Форум

 Математика
Математика

 2.6.1(3) Теория вероятности
2.6.1(3) Теория вероятности