Motokoss

Новичок
|
      
RKI Спасибо вам за решение, не могли бы еще решить одно ур-е.
Найдите общее решение диф. ур.

(Сообщение отредактировал Motokoss 8 марта 2010 15:59)
(Сообщение отредактировал Motokoss 8 марта 2010 15:59)
|
Всего сообщений: 17 | Присоединился: январь 2009 | Отправлено: 8 марта 2010 15:57 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: helena написал 7 марта 2010 21:58
Помогите пожалуйста найти частное решение дифференциального уравнения первого порядка, которое удовлетворяет заданному начальному условию:
(x^2-3y^2)dx+2xydy=0, y(2)=1.
Спасибо
dx + 2xydy = 0 )
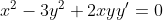


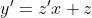
 = 0 )
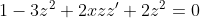
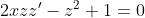
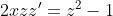
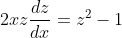
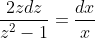
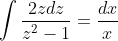
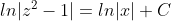
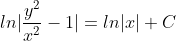
 = 1 )
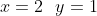
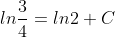
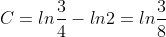
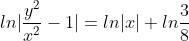
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 9 марта 2010 18:25 | IP
|
|
svetik2289

Новичок
|
      
помогите решить с третьего номера все!
внешняя ссылка удалена
заранее спасибо
|
Всего сообщений: 13 | Присоединился: октябрь 2009 | Отправлено: 9 марта 2010 19:02 | IP
|
|
Natalia 1919

Новичок
|
     
ПОМОГИТЕ!!!
^3=0)
(Сообщение отредактировал attention 13 марта 2010 20:04)
|
Всего сообщений: 4 | Присоединился: февраль 2010 | Отправлено: 13 марта 2010 19:14 | IP
|
|
attention 


Долгожитель
|
      
Цитата: Natalia 1919 написал 13 марта 2010 19:14
ПОМОГИТЕ!!!
^3=0)
Сделай замену: y'=p(y), y''=p(y)p'(y)
^3=0\Leftrightarrow\left\{\begin{gathered}y'=p(y),\hfill\\y''=p(y)p'(y)\hfill\\\end{gathered}\right\}\Leftrightarrow{pp'}+2yp^3=0\Leftrightarrow\hfill\\\Leftrightarrow\left[\begin{gathered}p=0,\hfill\\\frac{dp}{dy}=-2yp^2;\hfill\\\end{gathered}\right.\Leftrightarrow\left[\begin{gathered}y'=0,\hfill\\-\frac{dp}{p^2}=2ydy;\hfill\\\end{gathered}\right.\Leftrightarrow\left[\begin{gathered}y_1=C,\hfill\\-\int\frac{dp}{p^2}=2\int{y\,dy};\hfill\\\end{gathered}\right.\Leftrightarrow\hfill\\\end{gathered})
dy=\int{dx};\hfill\\\end{gathered}\right.\Leftrightarrow\left[\begin{gathered}y_1=C,\hfill\\\frac{y_2^3}{3}+C_1y_2=x+C_2.\hfill\\\end{gathered}\right.\hfill\\\end{gathered})
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 13 марта 2010 20:26 | IP
|
|
svetik2289

Новичок
|
      
помогите решить третий номер
внешняя ссылка удалена
заранее спасибо
|
Всего сообщений: 13 | Присоединился: октябрь 2009 | Отправлено: 13 марта 2010 20:47 | IP
|
|
Natalia 1919

Новичок
|
     
СПасибо огромное))))
|
Всего сообщений: 4 | Присоединился: февраль 2010 | Отправлено: 14 марта 2010 15:34 | IP
|
|
korp


Новичок
|
     
Помогите пожалуйста
Тема: диф. уравнения что допускают снижения порядка.
Найти общее решение диф. уравнения
1. 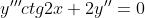
2. 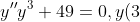=-7,%20y'(3)%20=%20-1)
|
Всего сообщений: 3 | Присоединился: март 2010 | Отправлено: 16 марта 2010 22:57 | IP
|
|
IKA

Новичок
|
     
Помогите,пожалуйста:
y'+2y=e^(-2x)
|
Всего сообщений: 6 | Присоединился: январь 2010 | Отправлено: 17 марта 2010 11:31 | IP
|
|
polinka

Новичок
|
      
Здравствуйте! Начала решать уравнение и запуталась с е сос тепенью помогите пожалуйста, вот уравнение y'+2xy=xe^(-x^2) дошла до int dv/v=-int2xdx
|
Всего сообщений: 7 | Присоединился: март 2010 | Отправлено: 17 марта 2010 13:17 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.3.1(2) Обыкновенные дифференциальные уравнения (ОДУ)
2.3.1(2) Обыкновенные дифференциальные уравнения (ОДУ)

 Форум
Форум

 Математика
Математика

 2.3.1(2) Обыкновенные дифференциальные уравнения (ОДУ)
2.3.1(2) Обыкновенные дифференциальные уравнения (ОДУ)