Nerev0r
Новичок
|
     
функция  является решением дифференциального уравнения  Тогда значение k равно …
(Сообщение отредактировал Nerev0r 27 окт. 2012 22:15)
|
Всего сообщений: 6 | Присоединился: октябрь 2012 | Отправлено: 27 окт. 2012 22:14 | IP
|
|
ustam
Долгожитель
|
Nerev0r
Найди производную y'. Потом подставь выражения для y и y' в дифф.уравнение и найдешь k
|
Всего сообщений: 420 | Присоединился: декабрь 2008 | Отправлено: 27 окт. 2012 22:55 | IP
|
|
maksim111
Новичок
|
Помогите решить диффур:
(x+y-2)dx+(x-y+4)dy=0
Но надо решить НЕ методом полного диффура!
не могу понять тип урь-е (исключая полный диф.)
|
Всего сообщений: 2 | Присоединился: ноябрь 2012 | Отправлено: 7 нояб. 2012 19:05 | IP
|
|
ustam
Долгожитель
|
maksim111
Так это и есть уравнение в полных дифференциалах и решать надо, как и положено решать такие уравнения. Зачем пытаться выдумывать что-то другое?
|
Всего сообщений: 420 | Присоединился: декабрь 2008 | Отправлено: 7 нояб. 2012 20:03 | IP
|
|
maksim111
Новичок
|
В этом вся и проблема! я доказал, что это полный диффур, решил, но препод сказала, определи тип урь-е и реши по-другому! Блин это однородное или нет? не могу я разобраться в нём, задрал пример...
|
Всего сообщений: 2 | Присоединился: ноябрь 2012 | Отправлено: 7 нояб. 2012 20:27 | IP
|
|
eliza91
Новичок
|
Помогите,пожалуйста:
y'''-16y'=e^2x+3cos(2x)-sin(x)
|
Всего сообщений: 1 | Присоединился: декабрь 2012 | Отправлено: 4 дек. 2012 3:30 | IP
|
|
MaxZenit
Новичок
|
Прошу помощи, надеюсь в ту тему кинул.
|
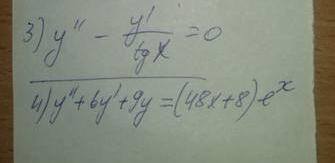
Всего сообщений: 2 | Присоединился: декабрь 2012 | Отправлено: 13 дек. 2012 18:18 | IP
|
|
lanafounteyn
Новичок
|
Ребят, помогите пожалуйста. Пишу курсовую по дифурам: вот такая просьба к тем, кто понимает ДУ:
я решила уравнение Y(t)=B*(dY(t)/dt)+C(t) в дискретном виде с помощью метода разделения переменных, вроде банально, при С(t)=0; мне необходимо решить это же уравнение с любыми значениями на ваш вкус, также при С(t)=0 и C(t)- const! пожалуйстаа помогите!
|
Всего сообщений: 1 | Присоединился: декабрь 2012 | Отправлено: 14 дек. 2012 20:33 | IP
|
|
MaxZenit
Новичок
|
с 3-им помогли:
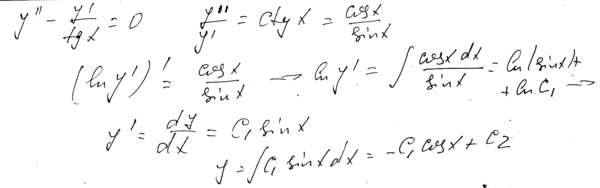
Ребят кто знает решение 4-ого?
|
Всего сообщений: 2 | Присоединился: декабрь 2012 | Отправлено: 15 дек. 2012 13:43 | IP
|
|
kettarian
Новичок
|
Помогите решить или подскажите идею решения:
y^{2}lny = y'^{2}+xyy'
x^{5}yy'+y^{4}=-x^{8}
y'=e^{\frac{(x+y}{2x-y+1}} +\frac{3y-1}{3x+1}
(Сообщение отредактировал kettarian 25 дек. 2012 0:54)
|
Всего сообщений: 1 | Присоединился: декабрь 2012 | Отправлено: 25 дек. 2012 0:52 | IP
|
|
Форум
2.3.1(2) Обыкновенные дифференциальные уравнения (ОДУ)
