statist


Новичок
|
     
Помогите пожалуйста - срочно надо!!!
1. Найти площадь части конической фигуры z=корень из (x*x+y*y), заключенной внутри цилиндра x^2+y^2=2x
2. Найти статический момент относительно плоскости Oxy однородного тела, ограниченного поверхностями
z= корень из (16-9*x*x-y*y)
6*z=9*x*x+y*y
3. Найти объем тела, заданого неравенствами
16≤x*x+y*y+z*z≤100
корень из ((x*x+y*y)/15)≤z≤корень из ((x*x+y*y)/3)
корень из 3 *x≤y≤0
|
Всего сообщений: 1 | Присоединился: июнь 2010 | Отправлено: 22 июня 2010 19:01 | IP
|
|
ZamZam


Новичок
|
     
∬x^2/y^2 dxdy, x=2, y=x, xy=1
помогите пожалуйста вычислить интеграл в wolfram mathematica
|
Всего сообщений: 2 | Присоединился: июнь 2010 | Отправлено: 25 июня 2010 15:15 | IP
|
|
ZamZam


Новичок
|
     
людииии, помогите с интегралом.......сессия горит!!!!
|
Всего сообщений: 2 | Присоединился: июнь 2010 | Отправлено: 26 июня 2010 17:18 | IP
|
|
attention 


Долгожитель
|
      
Цитата: Katrina написала 12 сентября 2010 20:36 здесь
Помогите кто-нибудь решить, пожалуйста!
Найти объем тела, ограниченного поверхностями:
z=sqrt(x^2+y^2); z=2-x^2-y^2
Katrina, данное тело снизу ограниченно конусом 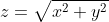 , а сверху параболоидом , а сверху параболоидом 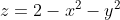 . Чтобы найти проекцию тела на плоскость x0y, приравняйте правые части уравнений ограничивающих поверхностей, то есть . Чтобы найти проекцию тела на плоскость x0y, приравняйте правые части уравнений ограничивающих поверхностей, то есть
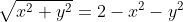
Теперь сделайте подстановку:
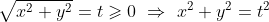
Получите квадратное уранение:
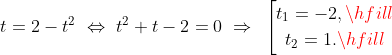
Следовательно, проекцией на плоскость x0y служит единичная окружность с центром в начале координат: 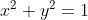
Теперь, когда известны пределы интегрирования, составляйте тройной интеграл для вычисления искомого объёма тела. Чтобы вычислить двойной интеграл перейдите в полярную систему координат.
dx\,dy=)
\,d\rho=)
}\right|_0^1=2\pi\!\left(1-\frac{1}{3}-\frac{1}{4}\right)=2\pi\cdot\frac{5}{12}=\frac{5\pi}{6}) (куб. ед.). (куб. ед.).
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 13 сен. 2010 17:09 | IP
|
|
Glouz

Новичок
|
     
Здравствуйте, помогите пожалуйста с решением двух тройных интегралов, буду очень вам благодарен или хотя бы дать наводку, как решать. Знаю, конечно, что примеры наверное "детские", но тем не менее, своих мозгов так сказать не хватает.
1. ∫∫∫ (x2 + y2 + z2)2dV
По области x2 + y2 + z2= 4
2. ∫∫∫ dV⁄√b2 + (x2 + y2 + z2)3/2 (квадратный корень в знаменателе под всем выражением)
По области x2 + y2 + z2= 4
|
Всего сообщений: 1 | Присоединился: сентябрь 2010 | Отправлено: 19 сен. 2010 23:49 | IP
|
|
attention 


Долгожитель
|
      
Glouz, в обоих интегралах надо перейти в сферические координаты.
Попробуйте, напишите что получается.
(Сообщение отредактировал attention 20 сен. 2010 14:10)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 20 сен. 2010 14:08 | IP
|
|
Sapfir

Новичок
|
     
Помогите пожалуйста с решением, уже неделю мучаюсь...
Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах a>0,
y^6=a^2*(3*y^2-x^2)*(x^2+y^2)
|
Всего сообщений: 1 | Присоединился: сентябрь 2010 | Отправлено: 28 сен. 2010 15:57 | IP
|
|
Annushka90

Новичок
|
      
помогите пожалуйста правильно найти пределы интегрирования и построить фигуру: найти объем тела, ограниченного поверхностями y=x^2, y=z, y+z=2
|
Всего сообщений: 1 | Присоединился: октябрь 2010 | Отправлено: 3 окт. 2010 15:16 | IP
|
|
koteshik

Новичок
|
      
Всем здравствуйте,я тут новенькая!!!
помогите пожалуйста кто-нибудь!!!я не знаю как решить!!!
с помощью двух двойных интегралов вычислить в полярных координатах площадь плоской фигуры, ограниченной указанными линиями:
(x^2+y^2)^3=a^4y^2
|
Всего сообщений: 2 | Присоединился: ноябрь 2010 | Отправлено: 5 нояб. 2010 17:38 | IP
|
|
koteshik

Новичок
|
      
блин,не правильно написала!!!
(x^2+y^2)^3=(a^4)*y^2
вот так думаю понятней будет...
|
Всего сообщений: 2 | Присоединился: ноябрь 2010 | Отправлено: 5 нояб. 2010 17:41 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.1.8 Кратные интегралы (двойные, тройные, ..., N-кратные)
2.1.8 Кратные интегралы (двойные, тройные, ..., N-кратные)

 Форум
Форум

 Математика
Математика

 2.1.8 Кратные интегралы (двойные, тройные, ..., N-кратные)
2.1.8 Кратные интегралы (двойные, тройные, ..., N-кратные)