ProstoVasya

Долгожитель
|
     
Haker0502
Эта замена переменных аналогична той, что мы с Вами обсуждали. Основная идея - подынтегральная функция должна зависеть от одной переменной. На прямых линиях ax+by = С подынтегральная функция постоянна. Таким образом надо ввести переменную, скажем t = ax+by или что-то подобное с точностью до умножения на число. В качестве другой переменной выберем семейство прямых ортогональное к выписанному ранее. Это, скажем, -bx +ay = s, с точностью до умножения на число. Это число выбираем так, чтобы якобиан равнялся 1. Это ортогональное преобразование плоскости, переводящее единичный круг в себя.
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 23 нояб. 2009 22:38 | IP
|
|
Haker0502


Участник
|
       
Цитата: ProstoVasya написал 23 нояб. 2009 22:38
t = ax+by или что-то подобное с точностью до умножения на число. -bx +ay = s, с точностью до умножения на число. Это число выбираем так, чтобы якобиан равнялся 1.
В моем случае, насколько я понял, это число равно
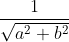
Отсюда,

Я правильно понял???
(Сообщение отредактировал Haker0502 23 нояб. 2009 23:01)
|
Всего сообщений: 109 | Присоединился: декабрь 2007 | Отправлено: 23 нояб. 2009 22:58 | IP
|
|
ProstoVasya

Долгожитель
|
     
Да, правильно. Это такой поворот плоскости, что подынтегральная функция зависит от одной переменной.
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 23 нояб. 2009 23:03 | IP
|
|
Haker0502


Участник
|
       
Цитата: ProstoVasya написал 23 нояб. 2009 23:03
Да, правильно. Это такой поворот плоскости, что подынтегральная функция зависит от одной переменной.
А число 1/sqrt(a^2+b^2) разве возможно подобрать простым перебором, в смысле, наугад? Или для этого есть определенные методы???
|
Всего сообщений: 109 | Присоединился: декабрь 2007 | Отправлено: 23 нояб. 2009 23:35 | IP
|
|
ProstoVasya

Долгожитель
|
     
Haker0502
Число sqrt(a^2+b^2) - длина векторов {a, b} и {-b, a}. Поэтому t и s - это проекции на новые координатные орты.
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 24 нояб. 2009 7:32 | IP
|
|
Haker0502


Участник
|
       
Цитата: ProstoVasya написал 24 нояб. 2009 7:32
Haker0502
Число sqrt(a^2+b^2) - длина векторов {a, b} и {-b, a}. Поэтому t и s - это проекции на новые координатные орты.
Спасибо большое, что бы я без Вас делал!
Помогите, пожалуста, готовлюсь к контрольной и не могу преодолеть двух заданий:
1.
}dxdy)
2.
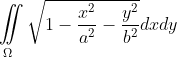 , где область , где область 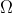 ограничена эллипсом ограничена эллипсом 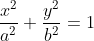
Относительно первого, у меня был похожий интеграл и вот как он сводился с помощью замены, а с этим так не получается — в результате выходит ноль.
}dxdy = \int\limits_{ - 1}^1 {f(u)du})
Помогите пожалуста. Огромное спасибо!
(Сообщение отредактировал attention 23 дек. 2009 10:38)
|
Всего сообщений: 109 | Присоединился: декабрь 2007 | Отправлено: 24 нояб. 2009 10:37 | IP
|
|
attention 


Долгожитель
|
      
Цитата: Haker0502 написал 27 нояб. 2009 19:18
Помогите, пожалуста, готовлюсь к контрольной и не могу преодолеть двух заданий:
1.
}dxdy)
2.
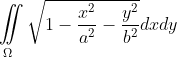 , где область , где область  ограничена эллипсом ограничена эллипсом 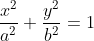
Относительно первого, у меня был похожий интеграл и вот как он сводился с помощью замены, а с этим так не получается — в результате выходит ноль.
}dxdy = \int\limits_{ - 1}^1 {f(u)du})
Помогите пожалуста. Огромное спасибо!
Подсказка для 1
 dx dy} = 4\int\limits_0^1 {dx\int\limits_0^{1 - x} {\left( {x + y} \right) dy} } = \ldots )
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 29 нояб. 2009 23:33 | IP
|
|
ProstoVasya

Долгожитель
|
     
Во втором интеграле выполните замену
x = a r cost
y = b r sint
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 30 нояб. 2009 20:09 | IP
|
|
Haker0502


Участник
|
       
Цитата: ProstoVasya написал 30 нояб. 2009 20:09
Во втором интеграле выполните замену
x = a r cost
y = b r sint
Извините меня за тупой вопрос: откуда Вы узнали, что надо делать именно такую замену?
|
Всего сообщений: 109 | Присоединился: декабрь 2007 | Отправлено: 30 нояб. 2009 21:02 | IP
|
|
ProstoVasya

Долгожитель
|
     
При a = b =1, Вы бы и сами сказали, что нужны полярные координаты.
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 30 нояб. 2009 21:05 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 2.1.8 Кратные интегралы (двойные, тройные, ..., N-кратные)
2.1.8 Кратные интегралы (двойные, тройные, ..., N-кратные)

 Форум
Форум

 Математика
Математика

 2.1.8 Кратные интегралы (двойные, тройные, ..., N-кратные)
2.1.8 Кратные интегралы (двойные, тройные, ..., N-кратные)