lilly


Новичок
|
     
Цитата: Haker0502 написал 5 нояб. 2009 1:24
Напишите пожалуста ярче (точнее) пределы интегралов, а то ничего не понять.
Простите...
вот сделала в paint

если не понятно снова переделаю
|
Всего сообщений: 30 | Присоединился: май 2009 | Отправлено: 5 нояб. 2009 2:55 | IP
|
|
1000HP


Новичок
|
      
RKI! Помоги с задачей!!! на 17 стр.
|
Всего сообщений: 12 | Присоединился: октябрь 2009 | Отправлено: 5 нояб. 2009 9:29 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: 1000HP написал 5 нояб. 2009 9:29
RKI! Помоги с задачей!!! на 17 стр.
Уравнение второй касательной Вы написали верно.
К сожалению, как искать угол между кривой и поверхностью я не помню. Это надо искать в специальной литературе (я думаю, по дифференциальной геометрии)
Цитата: lilly написал 5 нояб. 2009 2:55
Цитата: Haker0502 написал 5 нояб. 2009 1:24
Напишите пожалуста ярче (точнее) пределы интегралов, а то ничего не понять.
Простите...
вот сделала в paint

если не понятно снова переделаю
dy + \int\limits_{1}^{3} dx \int\limits_{0}^{\frac{3-x}{2} } f(x,y)dy = \iint\limits_{D} f(x,y)dxdy = )
Множество D - это область, ограниченная линиями 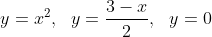 . .
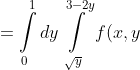dx )
(Сообщение отредактировал attention 23 дек. 2009 10:27)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 5 нояб. 2009 9:52 | IP
|
|
1000HP


Новичок
|
      
Жаль что угол не можете решить, я тоже нигде информацию найти не могу......
Парюсь с нахождением ротора....не понимаю.....всякую литературу почитал, нигде внятно не объсняется как его расчитывать.....
(Даны векторное поле F=(x+z)i и плоскость p=x+y+z-2=0 , которая совместно с координатными плоскостями образует пирамиду V. Обозначим основание пирамиды, принадлежащее плоскости (р), через , ограничивающий контур - через нормаль к направленную вне пирамиды V , - через n.
Требуется:
2) вычислить циркуляцию векторного поля F по замкнутому контуру непосредственно и применив теорему Стокса к контуру и ограниченной им поверхности с нормалью n;)
Непосредственно я посчитал, а ротор понять не могу...
Если сможете, поясните подробно, как этот пример решается....

(Сообщение отредактировал 1000HP 5 нояб. 2009 11:16)
|
Всего сообщений: 12 | Присоединился: октябрь 2009 | Отправлено: 5 нояб. 2009 11:13 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: 1000HP написал 5 нояб. 2009 11:13
Жаль что угол не можете решить, я тоже нигде информацию найти не могу......
Я сегодня обязательно поищу. Если найду, то сегодня-завтра напишу.
Цитата: 1000HP написал 5 нояб. 2009 11:13
(Даны векторное поле F=(x+z)i и плоскость p=x+y+z-2=0 , которая совместно с координатными плоскостями образует пирамиду V. Обозначим основание пирамиды, принадлежащее плоскости (р), через , ограничивающий контур - через нормаль к направленную вне пирамиды V , - через n.
Требуется:
2) вычислить циркуляцию векторного поля F по замкнутому контуру непосредственно и применив теорему Стокса к контуру и ограниченной им поверхности с нормалью n;)
Непосредственно я посчитал, а ротор понять не могу...
Если сможете, поясните подробно, как этот пример решается....

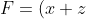i )
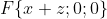
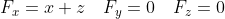
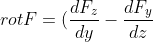i + (\frac{dF_{x} }{dz} - \frac{dF_{z} }{dx})j + (\frac{dF_{y} }{dx} - \frac{dF_{x} }{dy})k = )
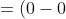i + (1 - 0)j + (0 - 0)k = j = \{ 0; 1; 0 \} )
Формулу ротора в расписанном виде можно посмотреть здесь
http://ru.wikipedia.org/wiki/%D0%A0%D0%BE%D1%82%D0%BE%D1%80_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0)
Цитата: 1000HP написал 2 нояб. 2009 10:27
Даны поверхность и кривая. Найти углы между ними в точках их пересечения. В этих же точках написать уравнение плоскости, касательной к поверхности.
Кривая: x=t; z=sint; y=t^2; Поверхность: 2*x^2+y^2=1
Появилась следующая идея.
Первая точка пересечения:
) )
 - параметр, соответствующий точке - параметр, соответствующий точке 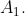
Напишем уравнение касательной прямой к кривой  в точке в точке 
 = 1 )
 = 1 )
 = 2t )
 = - 2\sqrt{\sqrt{2} - 1})
 = cost )
 = cos(-\sqrt{\sqrt{2} - 1}) = cos(\sqrt{\sqrt{2} - 1}) )
Уравнение касательной прямой имеет вид:
}{-2\sqrt{\sqrt{2} - 1} } = \frac{z + sin(\sqrt{2} - 1)}{cos{\sqrt{2} - 1} } )
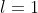
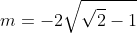
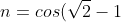 )
Касательная плоскость к заданной поверхности в точке  : :
y + 2 = 0 )

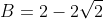
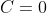
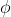 - угол между кривой и поверхностью в точке - угол между кривой и поверхностью в точке  или, другими словами, угол между касательной плоскостью к поверхности и касательной прямой к линии. или, другими словами, угол между касательной плоскостью к поверхности и касательной прямой к линии.
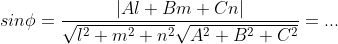 - подставить и посчитать - подставить и посчитать
Аналогично во второй точке
Надеюсь, что это верно
(Сообщение отредактировал attention 23 дек. 2009 10:27)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 5 нояб. 2009 11:30 | IP
|
|
FoxSov


Новичок
|
      
Помогите, пожалуйста.
Вычислить массу материальной пластины, занимающей область D плоскости хОу, если поверхностная плотность 
и границы области заданы уравнениями:  , ,  ,у=х. ,у=х.
Чертеж я сделала. А дальше не могу решить. Не могу перейти к полярным координатам.
(Сообщение отредактировал FoxSov 7 нояб. 2009 23:30)
|
Всего сообщений: 7 | Присоединился: август 2009 | Отправлено: 5 нояб. 2009 15:40 | IP
|
|
lilly


Новичок
|
     
RKI
СПАСИБО!!!
|
Всего сообщений: 30 | Присоединился: май 2009 | Отправлено: 6 нояб. 2009 7:14 | IP
|
|
beresnevvitaliy


Начинающий
|
       
RKI, пожалуйста помогите, очень спасибо заранее;)
Вычислить площадь, ограниченную линиями  (справа). (справа).

|
Всего сообщений: 52 | Присоединился: март 2009 | Отправлено: 6 нояб. 2009 19:29 | IP
|
|
1000HP


Новичок
|
      
Цитата: RKI написал 5 нояб. 2009 12:40
Цитата: 1000HP написал 2 нояб. 2009 10:27
Даны поверхность и кривая. Найти углы между ними в точках их пересечения. В этих же точках написать уравнение плоскости, касательной к поверхности.
Кривая: x=t; z=sint; y=t^2; Поверхность: 2*x^2+y^2=1
Появилась следующая идея.
Первая точка пересечения:
) )
 - параметр, соответствующий точке - параметр, соответствующий точке 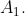
Напишем уравнение касательной прямой к кривой  в точке в точке 
 = 1 )
 = 1 )
 = 2t )
 = - 2\sqrt{\sqrt{2} - 1})
 = cost )
 = cos(-\sqrt{\sqrt{2} - 1}) = cos(\sqrt{\sqrt{2} - 1}) )
Уравнение касательной прямой имеет вид:
}{-2\sqrt{\sqrt{2} - 1} } = \frac{z + sin(\sqrt{2} - 1)}{cos{\sqrt{2} - 1} } )
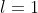
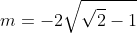
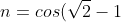 )
Касательная плоскость к заданной поверхности в точке  : :
y + 2 = 0 )

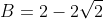
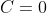
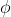 - угол между кривой и поверхностью в точке - угол между кривой и поверхностью в точке  или, другими словами, угол между касательной плоскостью к поверхности и касательной прямой к линии. или, другими словами, угол между касательной плоскостью к поверхности и касательной прямой к линии.
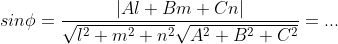 - подставить и посчитать - подставить и посчитать
Аналогично во второй точке
Надеюсь, что это верно
Подставив и посчитав приблизительно ( для точного вычисления не хватило бы терпения возится с корнями) получилось:
 (градусов наверно) (градусов наверно)
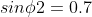 (градусов наверно) (градусов наверно)
|
Всего сообщений: 12 | Присоединился: октябрь 2009 | Отправлено: 7 нояб. 2009 15:35 | IP
|
|
RKI 


Долгожитель
|
     
100HP
Значения синуса НЕ МОГУТ быть градусами.
Это просто число
Для нахождения значения углов необходимо вычислить арксинусы от 0,29 и 0,7
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 7 нояб. 2009 15:51 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 2.1.8 Кратные интегралы (двойные, тройные, ..., N-кратные)
2.1.8 Кратные интегралы (двойные, тройные, ..., N-кратные)

 Форум
Форум

 Математика
Математика

 2.1.8 Кратные интегралы (двойные, тройные, ..., N-кратные)
2.1.8 Кратные интегралы (двойные, тройные, ..., N-кратные)