valynya

Новичок
|
     
проинтегрируйте уравнение
xdx+ydy+(ydx-xdy/x^2+y^2)=0
|
Всего сообщений: 2 | Присоединился: октябрь 2010 | Отправлено: 18 окт. 2010 21:21 | IP
|
|
Andregor


Новичок
|
      
Добрый вечер! НЕ могу решить уравнение: 2хуу'=(у')^2-1
|
Всего сообщений: 5 | Присоединился: март 2010 | Отправлено: 19 окт. 2010 20:42 | IP
|
|
Myteamix


Новичок
|
      

внешняя ссылка удалена
нужно срочно решить к завтрашнему дню
помогите пожалуйста!!
(Сообщение отредактировал Myteamix 21 окт. 2010 21:06)
(Сообщение отредактировал Myteamix 22 окт. 2010 0:06)
|
Всего сообщений: 40 | Присоединился: сентябрь 2010 | Отправлено: 21 окт. 2010 21:05 | IP
|
|
gip


Новичок
|
     
Помогите необходимо срочно решить диференцированное уровнение
ydx+(2корень xy-x) dy=0
Зарание спасибо
(Сообщение отредактировал gip 23 окт. 2010 13:22)
|
Всего сообщений: 2 | Присоединился: октябрь 2010 | Отправлено: 23 окт. 2010 13:21 | IP
|
|
gip


Новичок
|
     
Помогите срочно решить диференцированое уравнение второго порядка
y^^+7^+6y=0
|
Всего сообщений: 2 | Присоединился: октябрь 2010 | Отправлено: 23 окт. 2010 13:27 | IP
|
|
Vitani7


Новичок
|
      
Подскажите решение дифференциального уравнения второго порядка
2xy'y''=y'^2-1
(Сообщение отредактировал attention 24 окт. 2010 16:05)
|
Всего сообщений: 4 | Присоединился: октябрь 2010 | Отправлено: 24 окт. 2010 15:07 | IP
|
|
attention 


Долгожитель
|
      
Цитата: Vitani7 написал 24 окт. 2010 15:07
Подскажите решение дифференциального уравнения второго порядка
2xy'y''=y'^2-1
Перенесите y'^2 в левую часть и поделите уравнение на x^2, тогда слева можно будет выделить производную отношения (y'^2)/x, затем проинтегрируйте:
'=-\frac{1}{x^2}~\Rightarrow)
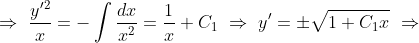
^3}.)
(Сообщение отредактировал attention 24 окт. 2010 16:09)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 24 окт. 2010 16:09 | IP
|
|
Vitani7


Новичок
|
      
attention, спасибо!
|
Всего сообщений: 4 | Присоединился: октябрь 2010 | Отправлено: 24 окт. 2010 17:10 | IP
|
|
Badsanta

Новичок
|
     
y``=x
y`(0)=1
y(0)=1
|
Всего сообщений: 4 | Присоединился: октябрь 2010 | Отправлено: 24 окт. 2010 19:09 | IP
|
|
attention 


Долгожитель
|
      
Цитата: Badsanta написал 24 окт. 2010 19:09
y''=x
y'(0)=1, y(0)=1
Badsanta, а с этим уравнением какие проблемы?!
Просто два раза проинтегрируйте его и ищите неизвестные константы:
\!dx=\frac{x^3}{6}+Cx+C_1.})
=1,y'(0)=1,\hfill\\y=\frac{x^3}{6}+Cx+C_1,\hfill\\y'=\frac{x^2}{2}+C;\hfill\\\end{gathered}\right.~\Rightarrow~\left\{\!\begin{gathered}1=C_1,\hfill\\1=C.\hfill\\\end{gathered}\right.})
Ответ: 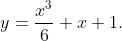
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 25 окт. 2010 0:01 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.3.1(2) Обыкновенные дифференциальные уравнения (ОДУ)
2.3.1(2) Обыкновенные дифференциальные уравнения (ОДУ)

 Форум
Форум

 Математика
Математика

 2.3.1(2) Обыкновенные дифференциальные уравнения (ОДУ)
2.3.1(2) Обыкновенные дифференциальные уравнения (ОДУ)