Sav

Новичок
|
     
Помогите решить:
Найти координаты центра тяжести однородной пластины,ограниченной линиями.Сделать чертеж
x^2+y^2=2^x;y>=0;x>=0
И вторая:
Перейдя к полярным координатам,вычислить двойной интеграл:
int int_{D}arctg y/x dxdy
|
Всего сообщений: 8 | Присоединился: январь 2009 | Отправлено: 11 окт. 2009 15:13 | IP
|
|
1000HP


Новичок
|
      
Помогите пожалуйста!!!
С помощью двойного интеграла вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертеж
y=sinx; y=1-x^2
спасибо))))
|
Всего сообщений: 12 | Присоединился: октябрь 2009 | Отправлено: 28 окт. 2009 13:13 | IP
|
|
ProstoVasya

Долгожитель
|
     
1000HP
Нет ли описки в условии задачи? Точки пересечения кривых находятся приближённо: х1 = -1.409624, х2 = 0.636733.
Площадь между кривыми с точностью до 6-го знака после запятой равна 1.670214
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 29 окт. 2009 10:00 | IP
|
|
beresnevvitaliy


Начинающий
|
       
Найти первообразную функцию U(x,y) по её полному дифференциалу:

(Сообщение отредактировал beresnevvitaliy 31 окт. 2009 15:52)
|
Всего сообщений: 52 | Присоединился: март 2009 | Отправлено: 31 окт. 2009 15:51 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: beresnevvitaliy написал 31 окт. 2009 15:51
Найти первообразную функцию U(x,y) по её полному дифференциалу:

(Сообщение отредактировал beresnevvitaliy 31 окт. 2009 15:52)
]dx + [e^{x+y} - cos(x-y) + 2]dy )
 = \int [e^{x+y} + cos(x-y)]dx + C(y) = )
 + C(y) )
 + C'(y) = e^{x+y} - cos(x-y) + 2 )
 = 2 )
 = 2y )
 = e^{x+y} + sin(x-y) + 2y )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 1 нояб. 2009 14:00 | IP
|
|
1000HP


Новичок
|
      
ProstoVasya нетб нет ошибки. Задачу решил, никто здесь не помог......
Помогите лучше вот с чем (искал теорию, нигде не нашел):
Даны поверхность и кривая. Найти углы между ними в точках их пересечения. В этих же точках написать уравнение плоскости, касательной к поверхности.
Кривая: x=t; z=sint; y=t^2; Поверхность: 2*x^2+y^2=1
(Сообщение отредактировал attention 23 дек. 2009 10:22)
|
Всего сообщений: 12 | Присоединился: октябрь 2009 | Отправлено: 2 нояб. 2009 10:26 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: 1000HP написал 2 нояб. 2009 10:27
Помогите лучше вот с чем (искал теорию, нигде не нашел):
Даны поверхность и кривая. Найти углы между ними в точках их пересечения. В этих же точках написать уравнение плоскости, касательной к поверхности.
Кривая: x=t; z=sint; y=t^2; Поверхность: 2*x^2+y^2=1
(Сообщение отредактировал 1000HP 2 нояб. 2009 10:31)
Найдем точки пересечения данной кривой и данной поверхности.
С одной стороны, данные точки лежат на кривой, то есть координаты этих точек имеют вид:
 . .
С другой стороны, данные точки лежат на поверхности, то есть координаты точек удовлетворяют уравнению:
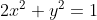
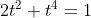
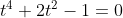
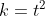
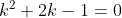



Таким образом, имеется две точки пересечения.
Первая точка:
) )
Вторая точка:
). )
Запишем уравнение плоскости в следующем виде:
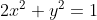
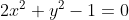
 = 2x^{2} + y^{2} - 1 )

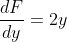
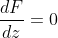
Запишем уравнение касательной плоскости к поверхности в первой точке.
 = - 4\sqrt{\sqrt{2} - 1} )
 = 2(\sqrt{2} - 1) )
 = 0 )
Уравнение первой касательной плоскости имеет вид:
 + 2(\sqrt{2} - 1)(y - (\sqrt{2} - 1)) + 0 = 0 )
y - 2 = 0 )
y + 2 = 0 )
Уравнение касательной плоскости во второй точке записывается аналогично
(Сообщение отредактировал RKI 2 нояб. 2009 13:32)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 2 нояб. 2009 13:30 | IP
|
|
1000HP


Новичок
|
      
Спасибо большое! Непонял где идет расчет углов(непонятно)...
Правильно я доделал?

|
Всего сообщений: 12 | Присоединился: октябрь 2009 | Отправлено: 2 нояб. 2009 14:59 | IP
|
|
lilly


Новичок
|
     
Может кто нибудь помочь с этим?

ЗАРАНЕЕ СПАСИБО!!!
|
Всего сообщений: 30 | Присоединился: май 2009 | Отправлено: 3 нояб. 2009 8:01 | IP
|
|
ProstoVasya

Долгожитель
|
     
lilly
Сомневаюсь, что тремя плоскостями можно огородить конечный объём.
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 3 нояб. 2009 8:46 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.1.8 Кратные интегралы (двойные, тройные, ..., N-кратные)
2.1.8 Кратные интегралы (двойные, тройные, ..., N-кратные)

 Форум
Форум

 Математика
Математика

 2.1.8 Кратные интегралы (двойные, тройные, ..., N-кратные)
2.1.8 Кратные интегралы (двойные, тройные, ..., N-кратные)