Graf de la Kruf


Новичок
|
     
Помогите плиз решить задачу:
Для тела, ограниченного заданными поверхностями, с помощью тройного интеграла найти объем. Сделать чертеж
z=0 x^2+y^2=z x^2+y^2=4
заранее благодарю)))
|
Всего сообщений: 25 | Присоединился: август 2009 | Отправлено: 24 авг. 2009 15:59 | IP
|
|
aly17

Участник
|
     
Roman Osipov
спасибо!!!
и можно вопрос))))в этом задании не нужно переходить к полярным координатам??
|
Всего сообщений: 107 | Присоединился: декабрь 2008 | Отправлено: 24 авг. 2009 22:40 | IP
|
|
attention 


Долгожитель
|
      
Цитата: Graf de la Kruf написал 24 авг. 2009 15:59
Помогите плиз решить задачу:
Для тела, ограниченного заданными поверхностями, с помощью тройного интеграла найти объем. Сделать чертеж
z=0 x^2+y^2=z x^2+y^2=4
заранее благодарю)))
Фактически Вам надо вычислить объем цилиндра  , который снизу ограничен плоскостью , который снизу ограничен плоскостью  , а сверху - параболоидом , а сверху - параболоидом  . .

(Сообщение отредактировал attention 3 сен. 2009 17:35)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 26 авг. 2009 12:33 | IP
|
|
Graf de la Kruf


Новичок
|
     
attention спасибо большое вы мне очень помогли!!!! )))
|
Всего сообщений: 25 | Присоединился: август 2009 | Отправлено: 26 авг. 2009 12:49 | IP
|
|
attention 


Долгожитель
|
      
Цитата: aly17 написал 23 авг. 2009 19:44
помогите пожалста с двойным интегралом!!
вычислить двойной интеграл:
int*int*xdxdy,где D - область,ограниченна линиями x^2+y^2 = 4, x=0, y=0 (x>=0,y>=0)
заранее огромное спасибо!!!
aly17, просто внести под дифференциал подкоренное выражение:

(Сообщение отредактировал attention 3 сен. 2009 17:35)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 27 авг. 2009 1:29 | IP
|
|
Graf de la Kruf


Новичок
|
     
Помогите пожалуйста!!!
С помощью двойного интеграла вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертеж
y=0.5; y=cos x
спасибо))))
(Сообщение отредактировал attention 23 дек. 2009 10:15)
|
Всего сообщений: 25 | Присоединился: август 2009 | Отправлено: 27 авг. 2009 12:32 | IP
|
|
attention 


Долгожитель
|
      
Цитата: Graf de la Kruf написал 1 сен. 2009 12:58
Помогите пожалуйста!!!
С помощью двойного интеграла вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертеж
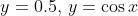
спасибо))))
Итак, имеем
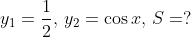
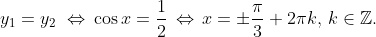
} \right| \, - \frac{\pi }{3} \leqslant x \leqslant \frac{\pi }{3},\, \frac{1}{2} \leqslant y \leqslant \cos x} \right\}. )
Следовательно, площадь  будет будет
dx = )
 \right|_0^{\pi /3} = 2k\left( \frac{\sqrt 3}{2} - \frac{\pi }{6}\right) = k\left( \sqrt 3 - \frac{\pi }{3} \right),)
где 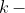 количество "арок" косинуса, лежащих выше одной второй. количество "арок" косинуса, лежащих выше одной второй.
График добавлю позже.
Это рассмотрен случай, когда косинус лежит выше одной второй, аналогично попробуйте рассмотреть случай, когда косинус лежит ниже одной второй.
(Сообщение отредактировал attention 3 сен. 2009 17:34)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 1 сен. 2009 15:27 | IP
|
|
beresnevvitaliy


Начинающий
|
       
 ; ;
 , если область D ограничена линиями xy=1, y=sqrt{x}, x=2 , если область D ограничена линиями xy=1, y=sqrt{x}, x=2
 , если область D ограничена x=0, y=0, 4x+4y-pi=0. , если область D ограничена x=0, y=0, 4x+4y-pi=0.
 , если область D определяется неравенствами x^2+y^2(<=)9, y(>=)(2/3)x+3. <= и >= соответственно меньше или равно, больше или равно. , если область D определяется неравенствами x^2+y^2(<=)9, y(>=)(2/3)x+3. <= и >= соответственно меньше или равно, больше или равно.
 , если область D ограничена линиями x=0, y=pi/2, y=x. , если область D ограничена линиями x=0, y=pi/2, y=x.
|
Всего сообщений: 52 | Присоединился: март 2009 | Отправлено: 12 сен. 2009 10:32 | IP
|
|
RKI 


Долгожитель
|
     
int_{1}^{3} dx int_{x^3}^{x} (x-y)dy =
= int_{1}^{3} (xy - (y^2)/2) |_{x^3}^{x} dx =
= int_{1}^{3} (x^2 - (x^2)/2 - x^4 + (x^6)/2) dx =
= int_{1}^{3} ((x^6)/2 - x^4 + (x^2)/2) dx =
= (x^7)/14 - (x^5)/5 + (x^3)/6 |_{1}^{3} =
= 2187/14 - 243/5 + 27/6 - 1/14 + 1/5 - 1/6 =
= 1093/7 - 242/5 + 13/3 = (16395 - 5082 + 455)/105 =
= 11768/105
надеюсь, я не ошиблась
int int_{D} (cos2x + siny) dxdy =
= int_{0}^{П/4} dy int_{0}^{П/4 - y} (cos2x + siny) dx =
= int_{0}^{П/4} ((1/2)sin2x + xsiny) |_{0}^{П/4 - y} dy =
= int_{0}^{П/4} ((1/2)sin(П/2 - 2y) + (П/4 - y)siny) dy =
= int_{0}^{П/4} ((1/2)cos2y + (П/4)siny - ysiny)dy =
= (1/4)sin2y - (П/4)cosy + ycosy - siny |_{0}^{П/4} =
= 1/4 - (П/4)(sqrt(2)/2) + (П/4)(sqrt(2)/2) - sqrt(2)/2 - 0 +
+ П/4 - 0 + 0 =
= 1/4 - sqrt(2)/2 + П/4
надеюсь, я не ошиблась
int int_{D} sin(x+y)dxdy =
= int_{0}^{П/2} dy int_{0}^{y} sin(x+y)dx =
= int_{0}^{П/2} - cos(x+y) |_{0}^{y} dy =
= int_{0}^{П/2} (- cos(y+y) + cos(0+y))dy =
= int_{0}^{П/2} (cosy - cos2y)dy =
= siny - (1/2)sin2y |_{0}^{П/2} =
= 1 - 0 - 0 + 0 = 1
надеюсь, я опять не ошиблась 
(Сообщение отредактировал attention 23 дек. 2009 10:17)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 12 сен. 2009 13:46 | IP
|
|
beresnevvitaliy


Начинающий
|
       
 , где ошибка не подскажете? , где ошибка не подскажете?
|
Всего сообщений: 52 | Присоединился: март 2009 | Отправлено: 13 сен. 2009 12:09 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 2.1.8 Кратные интегралы (двойные, тройные, ..., N-кратные)
2.1.8 Кратные интегралы (двойные, тройные, ..., N-кратные)

 Форум
Форум

 Математика
Математика

 2.1.8 Кратные интегралы (двойные, тройные, ..., N-кратные)
2.1.8 Кратные интегралы (двойные, тройные, ..., N-кратные)