malutka


Новичок
|
      
ммммм про меня забыли((((((
|
Всего сообщений: 16 | Присоединился: август 2009 | Отправлено: 1 сен. 2009 15:55 | IP
|
|
attention 


Долгожитель
|
      
Цитата: malutka написал 28 авг. 2009 10:22
Здравствуйте ))не могли бы помочь решить несколько задач)))))))))))
Имеются следующие выборочные данные (выборка 10%-ная, механическая) о выпуске продукции и сумме прибыли, млн. руб.:

По исходным данным:
Задание 13.1.
13.1.1. Постройте статистический ряд распределения предприятий по сумме прибыли, образовав пять групп с равными интервалами. Постройте графики ряда распределения.
Сначала надо проранжировать предприятия по сумме прибыли в пордке возрастания, что приведенно в таблице.
Теперь найдём длину группировочного интервала по формуле:

где 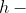 длина интервала; длина интервала;
 и и 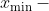 соотвественно максимальное и минимальное значение группировочного признака; соотвественно максимальное и минимальное значение группировочного признака;
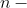 количество интервалов. количество интервалов.
Итак, вычислим длину группировочного интервала:
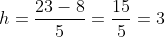

График ряда распределения предприятий по сумме прибыли

Задание 13.1.
13.1.2. Рассчитайте числовые характеристики ряда распределения предприятий по сумме прибыли: среднюю арифметическую , среднее квадратическое отклонение, дисперсию, коэффициент вариации V. Сделайте выводы.
На основе решения задания 13.1.1 (смотрите предыдущий пост) составим таблицу вспомогательных значений для расчета искомых величин.

Итак, рассчитаем искомые величины.
Средняя арифметическая:
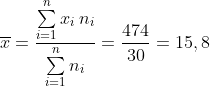
Среднее квадратическое отклонение:
^2 n_i}{ \sum\limits_{i = 1}^n n_i -1} = \sqrt \frac{168,3}{29} \approx \sqrt{5,803448276} \approx 2,409034719)
Дисперсия:
^2 \, n_i }{\sum\limits_{i = 1}^n n_i-1} = \frac{168,3}{29} \approx 5,803448276)
Коэффициент вариации:
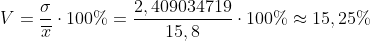
(Сообщение отредактировал attention 18 дек. 2009 18:44)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 1 сен. 2009 22:05 | IP
|
|
malutka


Новичок
|
      
спасибочки attention))))
просто я вообще в матиматике ни бум бум....а скоро сесия))))))
|
Всего сообщений: 16 | Присоединился: август 2009 | Отправлено: 1 сен. 2009 22:15 | IP
|
|
MADD


Начинающий
|
     
Помогите пожалуйста, решить такую задачу: Имеются следующие данные о распределении работников организации сферы обслуживания населения по размеру средней месячной заработной платы

Определить дисперсию заработной платы по способу моментов.
Формула такая? [tex]1/n \sum_{i=1}^n (x_i - M)^2[/tex] Не пойму, как считать, я дурак.
|
Всего сообщений: 65 | Присоединился: декабрь 2008 | Отправлено: 4 сен. 2009 2:36 | IP
|
|
Blondinka v kvadrate


Новичок
|
        
RKI, безумно благодарна за уже решенные задания! Вот уточненные (копирую из контрольной):
По данным выборки нужно:
1.Начертить график: полигон относительных частот и гистограмму.
2.Вычислить среднюю арифметическую, дисперсию, среднее квадратическое отклонение, коэффициенты асимметрии и эксцесса.
3.Построить эмпирическую функцию распределения и изобразить её графически.
4.На уровне значимости 0,05 проверить гипотезу о нормальном законе распределения генеральной совокупности.
1.1Распределение затрат на 100 руб. продукции по предприятиям хлопчатобумажной промышленности.
Интервал:
96,3-97,3 I 97,3-98,3 I 98,3-99,3 I 99,3-100,3 I 100,3-101,3 I 101,3-102,3 I 102,3-103,3 I 103,3-104,3 I 104,3-105,3
Кол-во Предприятий:
3 I 3 I 12 I 12 I 24 I 18 I 17 I 4 I 2
Она такая и есть...получается что не имеет решения?
RKI, и вот:
2.1 Найти интервальную оценку для генеральной средней и генерального среднего квадратического отклонения с надежностью 0,96 по следующим данным выборки: 12, 10, 13, 12, 15.
Все слово в слово.
RKI, право уже не ловко, но без вас здесь ни как:
2.5 Найти минимальный объем выборки , при котором с надежностью 0,9109 можно утверждать , что точность оценки генеральной средней диаметра изготовляемых валиков по выборочной средней будет равна 0,4 мм. Известно, что диаметр валиков генеральной совокупности есть нормальная случайная величина с Q = 3.2 мм.
Проверка статистических гипотез.
Общее для всех вариантов
1. По данным 12 рейсов установлено, что в среднем машина затрачивает на поездку до хлебоприемного комбината х =73 мин. Допустив, что время поездки есть нормальная случайная величина, на уровне значимости 0,05 проверить гипотезу Но: м(мю) =75 мин.:
а) При конкурирующей гипотезе Н1: м (мю) =72 мин., если известно, что Q=4 мин.;
б) При конкурирующей гипотезе H1: м(мю)=72 мин., если выборочное среднее квадратическое отклонение S=4 мин.;
в) Для условий а) и б) вычислить мощность критерия.
P.S. = Q(хвостик вверху,просто не знаю как называется)
(Сообщение отредактировал attention 18 дек. 2009 18:40)
|
Всего сообщений: 22 | Присоединился: июнь 2009 | Отправлено: 5 сен. 2009 18:37 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Blondinka v kvadrate написал 5 сен. 2009 18:40
2.1 Найти интервальную оценку для генеральной средней и генерального среднего квадратического отклонения с надежностью 0,96 по следующим данным выборки: 12, 10, 13, 12, 15.
xi 10 12 13 15
ni 1 2 1 1
x* - средняя в выборке
x* = (1/5)*(10*1 + 12*2 + 13*1 + 15*1) = 62/5 = 12.4
s - среднее квадратическое в выборке
s^2 = (1/5)*[1*(10 - 12.4)^2 + 2*(12 - 12.4)^2 +
+ 1*(13 - 12.4)^2 + 1*(15 - 12.4)^2] =
= (1/5)*(5.76 + 0.32 + 0.36 + 6.76) = (13.2)/5 = 2.64
s ~ 1.6248
X* - генеральная средняя
a = 0.96
t - критическая точка распределения Стьюдента с n-1 = 5-1 = 4 степенями свободы, на уровне значимости 1-a = 1-0.96 = 0.04
t ~ 2.9985
x* - st/sqrt(n) < X* < x* + st/sqrt(n)
12.4 - (1.6248)*(2.9985)/sqrt(5) < X* < 12.4 + (1.6248)*(2.9985)/sqrt(5)
12.4 - 2.1788 < X* < 12.4 + 2.1788
10.2212 < X* < 14.5788
б - генеральное средне квадратическое
a1 - критическая точки хи-квадрат распределения с n-1 = 5-1 = 4 степенями свободы, уровень значимости (1-a)/2 = (1-0.96)/2 = 0.02
a1 ~ 11.6678
a2 - критическая точки хи-квадрат распределения с n-1 = 5-1 = 4 степенями свободы, уровень значимости 1 - (1-a)/2 = 1 - (1-0.96)/2 = 1 - 0.02 = 0.98
a2 ~ 0.4294
(n-1)(s^2)/a1 < б^2 < (n-1)(s^2)/a2
4*(2.64)/(11.6678) < б^2 < 4*(2.64)/(0.4294)
0.9051 < б^2 < 24.5925
0.9514 < б < 4.9591
Цитата: Blondinka v kvadrate написал 5 сен. 2009 18:43
2.5 Найти минимальный объем выборки , при котором с надежностью 0,9109 можно утверждать , что точность оценки генеральной средней диаметра изготовляемых валиков по выборочной средней будет равна 0,4 мм. Известно, что диаметр валиков генеральной совокупности есть нормальная случайная величина с Q = 3.2 мм.
a = 0.9109
delta = 0.4
б = 3.2
delta > бu/sqrt(n)
Ф(u) = a/2 = (0.9109)/2 = 0.45545
u ~ 1.70
delta > бu/sqrt(n)
0.4 > (3.2)*(1.7)/sqrt(n)
0.4 > (5.44)/sqrt(n)
sqrt(n)/(5.44) > 1/(0.4)
sqrt(n) > (5.44)/(0.4)
sqrt(n) > 13.6
n > 184.96
n(min) = 185
Цитата: Blondinka v kvadrate написал 5 сен. 2009 18:52
1. По данным 12 рейсов установлено, что в среднем машина затрачивает на поездку до хлебоприемного комбината х =73 мин. Допустив, что время поездки есть нормальная случайная величина, на уровне значимости 0,05 проверить гипотезу Но: м(мю) =75 мин.:
а) При конкурирующей гипотезе Н1: м (мю) =72 мин., если известно, что Q=4 мин.;
б) При конкурирующей гипотезе H1: м(мю)=72 мин., если выборочное среднее квадратическое отклонение S=4 мин.;
x* = 73
а) H0: a = 75
H1: a = 72
б = 4
U = (73 - 75)sqrt(12)/4 ~ - 1.7321
Ф(u) = 0.5 - a = 0.5 - 0.05 = 0.45
u ~ 1.65
- 1.7321 < - 1.65
U < - u
Гипотеза H0 отвергается
б) H0: a = 75
H1: a = 72
s = 4
T = (73 - 75)sqrt(12)/4 ~ - 1.7321
t - критическая точка распределения Стьюдента с n-1 = 12-1 = 11 степенями свободы и уровнем значимости 0.05 для односторонней критической области.
t ~ 2.20
- 1.7321 > - 2.20
T > -t
Гипотеза H0 принимается
Цитата: Blondinka v kvadrate написал 5 сен. 2009 18:37
По данным выборки нужно:
1.Начертить график: полигон относительных частот и гистограмму.
2.Вычислить среднюю арифметическую, дисперсию, среднее квадратическое отклонение, коэффициенты асимметрии и эксцесса.
3.Построить эмпирическую функцию распределения и изобразить её графически.
4.На уровне значимости 0,05 проверить гипотезу о нормальном законе распределения генеральной совокупности.
1.1Распределение затрат на 100 руб. продукции по предприятиям хлопчатобумажной промышленности.
Интервал:
96,3-97,3 I 97,3-98,3 I 98,3-99,3 I 99,3-100,3 I 100,3-101,3 I 101,3-102,3 I 102,3-103,3 I 103,3-104,3 I 104,3-105,3
Кол-во Предприятий:
3 I 3 I 12 I 12 I 24 I 18 I 17 I 4 I 2
1.
x(i-1) - x(i) ni
96.3 - 97.3 3
97.3 - 98.3 3
98.3 - 99.3 12
99.3 - 100.3 12
100.3 - 101.3 24
101.3 - 102.3 18
102.3 - 103.3 17
103.3 - 104.3 4
104.3 - 105.3 2
n = 3 + 3 + 12 + 12 + 24 + 18 + 17 + 4 + 2 = 95
hi = x(i) - x(i-1)
частота wi = ni/n
плотность относительной частоты wi/hi
x(i-1) - x(i) ni hi wi wi/hi
96.3 - 97.3 3 1 3/95 3/95
97.3 - 98.3 3 1 3/95 3/95
98.3 - 99.3 12 1 12/95 12/95
99.3 - 100.3 12 1 12/95 12/95
100.3 - 101.3 24 1 24/95 24/95
101.3 - 102.3 18 1 18/95 18/95
102.3 - 103.3 17 1 17/95 17/95
103.3 - 104.3 4 1 4/95 4/95
104.3 - 105.3 2 1 2/95 2/95
Постороение гистограммы.
Олложим на оси абсцисс интервалы (96.3; 97.3); (97.3; 98.3); (98.3; 99.3); (99.3; 100.3); (100.3; 101.3); (101.3; 102.3); (102.3; 103.3); (103.3; 104.3); (104.3; 105.3) длиной 1 каждый.
Затем проведем параллельно им отрезки, отстоящие от оси x на соответствующие значения плотности относительной частоты: 3/95; 3/95; 12/95; 12/95; 24/95; 18/95; 17/95; 4/95; 2/95 соответственно.
Получится 9 рядом стоящих прямоугольников.
y(i) = (x(i-1) + x(i))/2
x(i-1) - x(i) ni hi wi wi/hi y(i)
96.3 - 97.3 3 1 3/95 3/95 96.8
97.3 - 98.3 3 1 3/95 3/95 97.8
98.3 - 99.3 12 1 12/95 12/95 98.8
99.3 - 100.3 12 1 12/95 12/95 99.8
100.3 - 101.3 24 1 24/95 24/95 100.8
101.3 - 102.3 18 1 18/95 18/95 101.8
102.3 - 103.3 17 1 17/95 17/95 102.8
103.3 - 104.3 4 1 4/95 4/95 103.8
104.3 - 105.3 2 1 2/95 2/95 104.8
Построение полигона относительных частот.
Поставить на координатной плоскости точки с координатами (96.3; 0); (96.8; 3/95); (97.8; 3/95); (98.8; 12/95); (99.8; 12/95); (100.8; 24/95); (101.8; 18/95); (102.8; 17/95); (103.8; 4/95); (104.8; 2/95); (105.3; 0). Соединить данные точки отрезками.
Получится ломаная кривая
(Сообщение отредактировал attention 18 дек. 2009 18:45)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 6 сен. 2009 11:53 | IP
|
|
attention 


Долгожитель
|
      
RKI, вроде бы, гистограмма строится не по относительным плотностям частот, а просто по частотам??
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 6 сен. 2009 14:27 | IP
|
|
RKI 


Долгожитель
|
     
attention
Перед решением данного пункта задачи я просмотрела книги по математической статистике, а также данные в интернете. И оказалось, что строить надо по относительным плотностям частот.
Цитата: Blondinka v kvadrate написал 6 сен. 2009 16:43
Огромное спасибо RKI!!! Как хорошо, что на земле есть очень одаренные люди!!!!Всех целую!)))
Ой, а я не знаю как надо строить, там не написано(( О_о
Тогда укажите, что гистограмма по относительным частотам, и стройте, как я описала.
Остальные пункты допишу завтра.
Цитата: Blondinka v kvadrate написал 5 сен. 2009 18:37
По данным выборки нужно:
1.Начертить график: полигон относительных частот и гистограмму.
2.Вычислить среднюю арифметическую, дисперсию, среднее квадратическое отклонение, коэффициенты асимметрии и эксцесса.
3.Построить эмпирическую функцию распределения и изобразить её графически.
4.На уровне значимости 0,05 проверить гипотезу о нормальном законе распределения генеральной совокупности.
1.1Распределение затрат на 100 руб. продукции по предприятиям хлопчатобумажной промышленности.
Интервал:
96,3-97,3 I 97,3-98,3 I 98,3-99,3 I 99,3-100,3 I 100,3-101,3 I 101,3-102,3 I 102,3-103,3 I 103,3-104,3 I 104,3-105,3
Кол-во Предприятий:
3 I 3 I 12 I 12 I 24 I 18 I 17 I 4 I 2
(продолжение)
2.
x(i-1) - x(i) ni y(i)
96.3 - 97.3 3 96.8
97.3 - 98.3 3 97.8
98.3 - 99.3 12 98.8
99.3 - 100.3 12 99.8
100.3 - 101.3 24 100.8
101.3 - 102.3 18 101.8
102.3 - 103.3 17 102.8
103.3 - 104.3 4 103.8
104.3 - 105.3 2 104.8
3*(96.8) + 3*(97.8) + 12*(98.8) + 12*(99.8) + 24*(100.8) +
+ 18*(101.8) + 17*(102.8) + 4*(103.8) + 2*(104.8) =
= 290.4 + 293.4 + 1185.6 + 1197.6 + 2419.2 + 1832.4 +
+ 1747.6 + 415.2 + 209.6 = 9591
среднее арифметическое x* = 9591/95 ~ 100.96
3*(96.8 - 100.96)^2 + 3*(97.8 - 100.96)^2 +
+ 12*(98.8 - 100.96)^2 + 12*(99.8 - 100.96)^2 +
+ 24*(100.8 - 100.96)^2 + 18*(101.8 - 100.96)^2 +
+ 17*(102.8 - 100.96)^2 + 4*(103.8 - 100.96)^2 +
+ 2*(104.8 - 100.96)^2 =
= 51.9168 + 29.9568 + 55.9872 + 16.1472 + 0.6144 +
+ 12.7008 + 57.5552 + 32.2624 + 29.4912 = 268.632
дисперсия s^2 ~ (268.632)/95 ~ 2.8277
квадратическое отклонение
s ~ 1.6816
3*(96.8 - 100.96)^3 + 3*(97.8 - 100.96)^3 +
+ 12*(98.8 - 100.96)^3 + 12*(99.8 - 100.96)^3 +
+ 24*(100.8 - 100.96)^3 + 18*(101.8 - 100.96)^3 +
+ 17*(102.8 - 100.96)^3 + 4*(103.8 - 100.96)^3 +
+ 2*(104.8 - 100.96)^3 ~
~ - 215.9739 - 94.6635 - 120.9324 - 18.7308 - 0.0983 +
+ 10.6687 + 105.9016 + 91.6252 + 113.2462 =
= - 128.9572
центральный момент третьего порядка
m(3) ~ - (128.9572)/95 ~ - 1.3574
коэффициент асимметрии
m(3)/(s^3) ~ - (1.3574)/(4.7550) ~ - 0.2855
3*(96.8 - 100.96)^4 + 3*(97.8 - 100.96)^4 +
+ 12*(98.8 - 100.96)^4 + 12*(99.8 - 100.96)^4 +
+ 24*(100.8 - 100.96)^4 + 18*(101.8 - 100.96)^4 +
+ 17*(102.8 - 100.96)^4 + 4*(103.8 - 100.96)^4 +
+ 2*(104.8 - 100.96)^4 ~
~ 898.4514 + 299.1366 + 261.2139 + 21.7277 + 0.0157 +
+ 8.9617 + 194.8589 + 260.2156 + 434.8654 =
~ 2379.2355
центральный момент четвертого порядка
m(4) ~ (2379.2355)/95 ~ 25.0445
коэффициент эксцесса
m(4)/(s^4) - 3 ~ (25.0445)/(7.9959) - 3 ~ 0.1321
Цитата: Blondinka v kvadrate написал 5 сен. 2009 18:37
По данным выборки нужно:
1.Начертить график: полигон относительных частот и гистограмму.
2.Вычислить среднюю арифметическую, дисперсию, среднее квадратическое отклонение, коэффициенты асимметрии и эксцесса.
3.Построить эмпирическую функцию распределения и изобразить её графически.
4.На уровне значимости 0,05 проверить гипотезу о нормальном законе распределения генеральной совокупности.
1.1Распределение затрат на 100 руб. продукции по предприятиям хлопчатобумажной промышленности.
Интервал:
96,3-97,3 I 97,3-98,3 I 98,3-99,3 I 99,3-100,3 I 100,3-101,3 I 101,3-102,3 I 102,3-103,3 I 103,3-104,3 I 104,3-105,3
Кол-во Предприятий:
3 I 3 I 12 I 12 I 24 I 18 I 17 I 4 I 2
(продолжение)
3.
F(x) = {0, x <= 96.8
{3/95, 96.8 < x <= 97.8
{6/95, 97.8 < x <= 98.8
{18/95, 98.8 < x <= 99.8
{30/95, 99.8 < x <= 100.8
{54/95, 100.8 < x <= 101.8
{72/95, 101.8 < x <= 102.8
{89/95, 102.8 < x <= 103.8
{93/95, 103.8 < x <= 104.8
{1, x > 104.8
Цитата: Blondinka v kvadrate написал 5 сен. 2009 18:37
По данным выборки нужно:
1.Начертить график: полигон относительных частот и гистограмму.
2.Вычислить среднюю арифметическую, дисперсию, среднее квадратическое отклонение, коэффициенты асимметрии и эксцесса.
3.Построить эмпирическую функцию распределения и изобразить её графически.
4.На уровне значимости 0,05 проверить гипотезу о нормальном законе распределения генеральной совокупности.
1.1Распределение затрат на 100 руб. продукции по предприятиям хлопчатобумажной промышленности.
Интервал:
96,3-97,3 I 97,3-98,3 I 98,3-99,3 I 99,3-100,3 I 100,3-101,3 I 101,3-102,3 I 102,3-103,3 I 103,3-104,3 I 104,3-105,3
Кол-во Предприятий:
3 I 3 I 12 I 12 I 24 I 18 I 17 I 4 I 2
(продолжение)
4.
i x(i-1) - x(i) ni y(i)
1 96.3 - 97.3 3 96.8
2 97.3 - 98.3 3 97.8
3 98.3 - 99.3 12 98.8
4 99.3 - 100.3 12 99.8
5 100.3 - 101.3 24 100.8
6 101.3 - 102.3 18 101.8
7 102.3 - 103.3 17 102.8
8 103.3 - 104.3 4 103.8
9 104.3 - 105.3 2 104.8
x* ~ 100.96
s ~ 1.6816
p1 = P(X < 96.8) = 0.5 + Ф((96.8 - 100.96)/1.6816) ~
~ 0.5 + Ф(-2.47) = 0.5 - Ф(2.47) ~ 0.5 - 0.493 = 0.007
p2 = P(96.8 < X < 97.8) =
= Ф((97.8 - 100.96)/1.6816) - Ф((96.8 - 100.96)/1.6816) ~
~ Ф(-1.88) - Ф(-2.47) = - Ф(1.88) + Ф(2.47) ~
~ - 0.4699 + 0.493 = 0.0231
p3 = P(97.8 < X < 98.8) =
= Ф((98.8 - 100.96)/1.6816) - Ф((97.8 - 100.96)/1.6816) ~
~ Ф(-1.28) - Ф(-1.88) = - Ф(1.28) + Ф(1.88) ~
~ - 0.3997 + 0.4699 = 0.0702
p4 = P(98.8 < X < 99.8) =
= Ф((99.8 - 100.96)/1.6816) - Ф((98.8 - 100.96)/1.6816) ~
~ Ф(-0.69) - Ф(-1.28) = - Ф(0.69) + Ф(1.28) ~
~ - 0.2549 + 0.3997 = 0.1448
p5 = P(99.8 < X < 100.8) =
= Ф((100.8 - 100.96)/1.6816) - Ф((99.8 - 100.96)/1.6816) ~
~ Ф(-0.10) - Ф(-0.69) = - Ф(0.10) + Ф(0.69) ~
~ - 0.0398 + 0.2549 = 0.2151
p6 = P(100.8 < X < 101.8) =
= Ф((101.8 - 100.96)/1.6816) - Ф((100.8 - 100.96)/1.6816) ~
~ Ф(0.50) - Ф(-0.10) = Ф(0.50) + Ф(0.10) ~
~ 0.1915 + 0.0398 = 0.2313
p7 = P(101.8 < X < 102.8) =
= Ф((102.8 - 100.96)/1.6816) - Ф((101.8 - 100.96)/1.6816) ~
~ Ф(1.09) - Ф(0.50) ~ 0.3621 - 0.1915 = 0.1706
p8 = P(102.8 < X < 103.8) =
= Ф((103.8 - 100.96)/1.6816) - Ф((102.8 - 100.96)/1.6816) ~
~ Ф(1.69) - Ф(1.09) ~ 0.4545 - 0.3621 = 0.0924
p9 = P(X > 103.8) = 0.5 - Ф((103.8 - 100.96)/1.6816) ~
~ 0.5 - Ф(1.69) ~ 0.5 - 0.4545 = 0.0455
i x(i-1) - x(i) ni pi npi
1 96.3 - 97.3 3 0.007 0.665
2 97.3 - 98.3 3 0.0231 2.1945
3 98.3 - 99.3 12 0.0702 6.669
4 99.3 - 100.3 12 0.1448 13.756
5 100.3 - 101.3 24 0.2151 20.4345
6 101.3 - 102.3 18 0.2313 21.9735
7 102.3 - 103.3 17 0.1706 16.207
8 103.3 - 104.3 4 0.0924 8.778
9 104.3 - 105.3 2 0.0455 4.3225
i x(i-1) - x(i) ni npi ni - npi
1 96.3 - 97.3 3 0.665 2.335
2 97.3 - 98.3 3 2.1945 0.8055
3 98.3 - 99.3 12 6.669 5.331
4 99.3 - 100.3 12 13.756 - 1.756
5 100.3 - 101.3 24 20.4345 3.5655
6 101.3 - 102.3 18 21.9735 - 3.9735
7 102.3 - 103.3 17 16.207 0.793
8 103.3 - 104.3 4 8.778 - 4.778
9 104.3 - 105.3 2 4.3225 - 2.3225
i x(i-1) - x(i) npi ni - npi (ni - npi)^2/npi
1 96.3 - 97.3 0.665 2.335 8.1988
2 97.3 - 98.3 2.1945 0.8055 0.2957
3 98.3 - 99.3 6.669 5.331 4.2614
4 99.3 - 100.3 13.756 - 1.756 0.2242
5 100.3 - 101.3 20.4345 3.5655 0.6221
6 101.3 - 102.3 21.9735 - 3.9735 0.7185
7 102.3 - 103.3 16.207 0.793 0.0388
8 103.3 - 104.3 8.778 - 4.778 2.6007
9 104.3 - 105.3 4.3225 - 2.3225 1.2479
Суммируя значения в последней графе, получаем значение статистики хи квадрат 18.2081.
Из таблицы критических точек распределения хи-квадрат по уровню значимости 0,05 и числу степеней свободы r-1-k = 9-1-2=6 находим критическую точку 12.6.
Поскольку 18.2081 > 12.6, то гипотеза о нормальном законе распределения генеральной совокупности НЕ принимается.
(Сообщение отредактировал attention 18 дек. 2009 18:48)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 6 сен. 2009 14:41 | IP
|
|
attention 


Долгожитель
|
      
Нашел у себя в книге, что полигон и гистограмма могут строятся как по относительным, так и не по относительным частотам (Сизова Т.М. Статистика).
Blondinkе v kvadrate надо было бы уточнить, по каким частотам строить гистограмму: абсолютным или относительным.
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 6 сен. 2009 14:55 | IP
|
|
RKI 


Долгожитель
|
     
По сути, изменения в построении будут несложными
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 6 сен. 2009 15:08 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 2.6.3 Математическая статистика
2.6.3 Математическая статистика

 Форум
Форум

 Математика
Математика

 2.6.3 Математическая статистика
2.6.3 Математическая статистика