elena59


Новичок
|
     
Подсскажите, пожалуйста, решение этого задания!!! не получаеться решить!
Дана функция y=f(x) и два значения аргумента х .
Требуется.
1)Найти пределы функций при приближении к каждому из данных значений х слева и справа;
2) Установить , является ли данная функция непрерывной или разрывной для каждого из данных значений х;
3) Сделать схематический чертеж в окрестности точек x1 и x2.
y=9^(1/(2-x)); x1=0; x2=2;
|
Всего сообщений: 2 | Присоединился: март 2010 | Отправлено: 9 марта 2010 20:42 | IP
|
|
Innesa


Новичок
|
     
Очень прошу ребят подскажите пожалуйста!!!!!
Функция задается различными аналитическими выражениями для различных областей изменения независимой переменной.
Требуется.
1) Найти точки разрыва функции, если они существуют;
2) Найти скачок функции в каждой точке разрыва;
3) Сделать схематический чертеж.
пример: -2(x+1), если x<=-1
y= (x+1)^2, если -1<x<0
x, если x=>0
|
Всего сообщений: 3 | Присоединился: март 2010 | Отправлено: 9 марта 2010 21:12 | IP
|
|
elena59


Новичок
|
     
Большое спасибо!
А подскажите пожалуйста !!!
Найти указанные пределы ( не пользуясь правилом Лопиталя );
1) 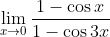
2) ^{\tfrac{3x}{x-1}})
(Сообщение отредактировал attention 11 марта 2010 8:47)
|
Всего сообщений: 2 | Присоединился: март 2010 | Отправлено: 10 марта 2010 18:14 | IP
|
|
attention 


Долгожитель
|
      
Цитата: elena59 написал 10 марта 2010 17:14
Большое спасибо!
А подскажите пожалуйста !!!
Найти указанные пределы ( не пользуясь правилом Лопиталя );
1) 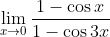
Преобразуйте числитель и знаменатель к первому замечательному пределу:
^2 = \frac{1}{9}\left(\frac{1}{1}\right)^2 = \frac{1}{9}. \hfill \\ \end{gathered})
(Сообщение отредактировал attention 11 марта 2010 9:08)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 11 марта 2010 10:04 | IP
|
|
attention 


Долгожитель
|
      
Цитата: elena59 написал 10 марта 2010 17:14
Большое спасибо!
А подскажите пожалуйста !!!
Найти указанные пределы ( не пользуясь правилом Лопиталя );
2) ^{\tfrac{3x}{x-1}})
Преобрвзуйте ко второму замечательному пределу:
^{\tfrac{3x}{x-1}}=\mathop{\lim}\limits_{x\to1}(1+2x-2)^{\tfrac{6x}{2x-2}}=\left[\mathop{\lim}\limits_{x\to1}(1+2x-2)^{\tfrac{1}{2x-2}}\right]^{6\mathop{\lim}\limits_{x\to1}x}=e^6.)
(Сообщение отредактировал attention 11 марта 2010 9:24)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 11 марта 2010 10:22 | IP
|
|
vika

Новичок
|
      
Помогите найти придел lim (x->беск,y->2) (1+y/x)^x
заранее спасибо
|
Всего сообщений: 5 | Присоединился: декабрь 2009 | Отправлено: 11 марта 2010 19:24 | IP
|
|
Karim


Начинающий
|
      
Помогите пожалуйста с пределом
(х^2*ctg 2х)/sin 3х
если х->0
|
Всего сообщений: 86 | Присоединился: октябрь 2009 | Отправлено: 12 марта 2010 0:40 | IP
|
|
Karim


Начинающий
|
      
Я кажется уже решил сам, так что не надо мне помогать
|
Всего сообщений: 86 | Присоединился: октябрь 2009 | Отправлено: 12 марта 2010 1:21 | IP
|
|
Roman Osipov 


Долгожитель
|
         
На всякий случай: ответ 1/6.
внешняя ссылка удалена.
|
Всего сообщений: 2356 | Присоединился: май 2007 | Отправлено: 17 марта 2010 21:53 | IP
|
|
Snigur


Новичок
|
     
Доброй ночи! Помогите пожалуйста
lim (1-2х)^1/х,
если х->0
|
Всего сообщений: 19 | Присоединился: июль 2009 | Отправлено: 5 апр. 2010 0:43 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.1.2 Предел функции одного и многих действ. аргументов
2.1.2 Предел функции одного и многих действ. аргументов

 Форум
Форум

 Математика
Математика

 2.1.2 Предел функции одного и многих действ. аргументов
2.1.2 Предел функции одного и многих действ. аргументов