senara

Новичок
|
    
RKI очень вас прошу о помощи. Надо контрольную сдавать, из 9 заданий смогла с горем пополам решить 2 (транспортные задачи). Видимо не тот мозг у меня! Очень на вас надеюсь, очень прошу о понимании. Задания следующие:
1. На фирме работают 8 аудиторов, из которых 3 – высокой квалификации, и 5 программистов, из которых 2 – высокой квалификации. В командировку надо отправить группу из 3 аудиторов и 2 программистов. Какова вероятность того, что в этой группе окажется по крайней мере 1 аудитор высокой квалификации, если каждый специалист имеет равные возможности поехать в командировку?
2. Прибор, работающий в течение времени t, состоит из трех узлов, каждый из которых независимо от других может за это время выйти из строя. Неисправность хотя бы одного узла выводит прибор из строя целиком. Вероятность безотказной работы в течение времени t первого узла равна – 0,9, второго – 0,95, третьего – 0,8. Найти вероятность того, что в течение времени t прибор выйдет из строя.
3. Известно, что в среднем 60 % всего числа изготовляемых заводом телефонных аппаратов является продукцией первого сорта. Чему равна вероятность того, что в изготовленной партии окажется: а) 6 аппаратов первого сорта, если партия содержит 10 аппаратов; б) 120 аппаратов первого сорта, если партия содержит 200 аппаратов?
4. Два покупателя независимо друг от друга делают по одной покупке. Вероятность того, что покупку сделает первый покупатель, равна 0,8, а вероятность того, что второй – 0,6. Случайная величина Х – число покупок, сделанных покупателями. Описать закон распределения случайной величины Х. Найти функцию распределения случайной величины и ее числовые характеристики.
5. Случайная величина Х задана интегральной функцией F (х) = 0. Найти:
1)Дифференциальную функцию распределения вероятностей f(x);
2)Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение;
3)Вычислить вероятность попадания случайной величины в заданный интервал (λ, β);
4)Построить графики функций F(x) = 0 и f(x).
0, х ≤ 0
F(x) (х^2)/9, 0 < х ≤ 3
1, х > 3.
λ = 2, β = 3
6. имеются данные о продаже товаров в системе спорткультторга по кварталам пятилетки в тыс.руб. Рассчитать гарантийный запас товара (в тыс.руб) на квартал с указанной надежностью и проанализировать плановые товарные запасы на квартал.
Данные о продаже одежды и белья трикотажного:
313299330300460534300331235
206222380403328350236232299
7. По данным предприятий между капиталовложениями Х (млн.руб) и выпуском продукции Y (млн.руб) найти выборочное уравнение прямой линии регрессии Y на Х и статистическими методами изучить зависимость между случайными величинами.
хi yi
20 + N/2 32 – K/2
24 + M/2 30 – N/2
28 + K/2 36 – M/2
30 + N/2 40 – K/2
31 + K/2 41 – M/2
33 + M/2 47 – N/2
34 + K/2 56 – N/2
37 + N/2 54 – M/2
38 + M/2 60 – K/2
40 + K/2 55 – M/2
41 + N/2 61 – N/2
43 + M/2 67 - K/2
45 + K/2 69 – M/2
48 + M/2 76 – K/2
Где: M = 44; N = 52; K = 24
Y = 0,97, план 3,75 тыс. у.е.
Очень рассчитываю на вас.
|
Всего сообщений: 7 | Присоединился: январь 2010 | Отправлено: 8 фев. 2010 7:52 | IP
|
|
senara

Новичок
|
    
5 задание отбразилось не корректно.
3)Вычислить вероятность попадания случайной величины в заданный интервал (альфа;бетта;)
0, х меньше или равно 0
F(x) (х^2)/9, 0 < х меньше или равно 3
1, х > 3.
альфа= 2, бетта= 3
|
Всего сообщений: 7 | Присоединился: январь 2010 | Отправлено: 8 фев. 2010 8:01 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: senara написал 8 фев. 2010 7:52
2. Прибор, работающий в течение времени t, состоит из трех узлов, каждый из которых независимо от других может за это время выйти из строя. Неисправность хотя бы одного узла выводит прибор из строя целиком. Вероятность безотказной работы в течение времени t первого узла равна – 0,9, второго – 0,95, третьего – 0,8. Найти вероятность того, что в течение времени t прибор выйдет из строя.
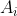 = {вероятность безотказной работы в течение времени t i-того узла} = {вероятность безотказной работы в течение времени t i-того узла}
i = 1, 2, 3
 = 0.9 )
 = 0.95 )
 = 0.8 )
A = {в течение времени t прибор выйдет из строя}
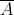 = {в течение времени t прибор не выйдет из строя} = {в течение времени t прибор не выйдет из строя}
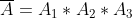
 = P(A_{1}*A_{2}*A_{3}) = P(A_{1})*P(A_{2})*P(A_{3}) = )
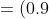*(0.95)*(0.8) = 0.684 )
 = 1 - P(\overline{A}) = 1 - 0.684 = 0.316 )
(Сообщение отредактировал RKI 8 фев. 2010 11:42)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 8 фев. 2010 11:41 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: senara написал 8 фев. 2010 7:52
3. Известно, что в среднем 60 % всего числа изготовляемых заводом телефонных аппаратов является продукцией первого сорта. Чему равна вероятность того, что в изготовленной партии окажется: а) 6 аппаратов первого сорта, если партия содержит 10 аппаратов; б) 120 аппаратов первого сорта, если партия содержит 200 аппаратов?
p = 0.6 - вероятность того, что аппарат является продукцией первого сорта
q = 1 - p = 0.4
а) n = 10 - общее количество аппаратов
m - количество аппаратов первого сорта
По формуле Бернулли
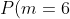 = C_{10}^{6}*(0.6)^{6}*(0.4)^{4} = )
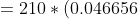*(0.0256) = 0.250822656 )
б) n = 200 - общее количество аппаратов
np = 200*(0.6) = 120
npq = 200*(0.6)*(0.4) = 48
m - количество аппаратов первого сорта
m = 120
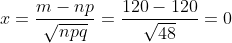
По локальной формуле Муавра-Лапласа
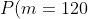 = \frac{\phi (x) }{\sqrt{npq} } = \frac{\phi (0)}{\sqrt{48} } \sim \frac{0.39894}{\sqrt{48} } \sim 0.0576 )
(Сообщение отредактировал RKI 8 фев. 2010 12:00)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 8 фев. 2010 11:59 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: senara написал 8 фев. 2010 7:52
4. Два покупателя независимо друг от друга делают по одной покупке. Вероятность того, что покупку сделает первый покупатель, равна 0,8, а вероятность того, что второй – 0,6. Случайная величина Х – число покупок, сделанных покупателями. Описать закон распределения случайной величины Х. Найти функцию распределения случайной величины и ее числовые характеристики.
Случайная величина X - число покупок. Данная случайная величина может принимать следующие значения:
{X=0} - ни один из двух покупателей не совершил покупку
{X=1} - покупку совершил только один покупатель
{X=2} - оба покупателя совершили по покупке
P(X=0) = (1-0.8)*(1-0.6) = (0.2)*(0.4) = 0.08
P(X=1) = (0.8)*(1-0.6) + (1-0.8)*(0.6) =
= (0.8)*(0.4) + (0.2)*(0.6) = 0.32 + 0.12 = 0.44
P(X=2) = (0.8)*(0.6) = 0.48
Закон распределения случайной величины X имеет вид:
X 0 1 2
P 0.08 0.44 0.48
Функция распределения случайной величины X имеет вид:
F(x) = {0, x <= 0
{0.08, 0 < x <= 1
{0.52, 1 < x <= 2
{1, x > 2
M(X) = 0*(0.08) + 1*(0.44) + 2*(0.48) = 0 + 0.44 + 0.96 = 1.4 - математическое ожидание
 ) = 0*(0.08) + 1*(0.44) + 4*(0.48) = 0 + 0.44 + 1.92 = 2.36 = 0*(0.08) + 1*(0.44) + 4*(0.48) = 0 + 0.44 + 1.92 = 2.36
 = M(X^{2}) - M^{2} (X) = 2.36 - 1.96 = 0.4 ) - дисперсия - дисперсия
 = \sqrt{D(X)} = \sqrt{0.4} \sim 0.6325 ) - среднее квадратическое отклонение - среднее квадратическое отклонение
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 8 фев. 2010 12:09 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: senara написал 8 фев. 2010 7:52
5. Случайная величина Х задана интегральной функцией F (х) = 0. Найти:
1)Дифференциальную функцию распределения вероятностей f(x);
2)Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение;
3)Вычислить вероятность попадания случайной величины в заданный интервал (λ, β);
4)Построить графики функций F(x) = 0 и f(x).
F(x) = {0, x <= 0
{(x^2)/9, 0 < x <= 3
{1, x > 3
1) f(x) = F'(x)
f(x) = {0, x <= 0
{2x/9, 0 < x < 3
{0, x > 3
2)
 = \int\limits_{-\infty}^{+\infty} xf(x)dx = \int\limits_{-\infty}^{0} xf(x)dx + \int\limits_{0}^{3} xf(x)dx + \int\limits_{3}^{+\infty} xf(x)dx = )

 = 2 )
 = \int\limits_{-\infty}^{+\infty} x^{2}f(x)dx = \int\limits_{-\infty}^{0} x^{2}f(x)dx + \int\limits_{0}^{3} x^{2}f(x)dx + \int\limits_{3}^{+\infty} x^{2}f(x)dx = )
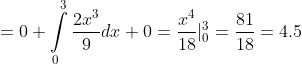
 = M(X^{2}) - M^{2}(X) = 4.5 - 4 = 0.5 )
 = \sqrt{D(X)} = \sqrt{0.5} \sim 0.7071 )
3) P(2<X<3) = F(3) - F(2) = 1 - 4/9 = 5/9
(Сообщение отредактировал RKI 8 фев. 2010 12:34)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 8 фев. 2010 12:31 | IP
|
|
senara

Новичок
|
    
Огромнейшее ВАМ спасибо за помощь! Если вам не сложно, можно решить еще 7 задание? Я очень - очень вам БЛАГОДАРНА!!
|
Всего сообщений: 7 | Присоединился: январь 2010 | Отправлено: 8 фев. 2010 13:11 | IP
|
|
|
|
|

 Форум
Форум

 Математика
Математика

 2.6.2 Теория вероятностей в примерах
2.6.2 Теория вероятностей в примерах

 Форум
Форум

 Математика
Математика

 2.6.2 Теория вероятностей в примерах
2.6.2 Теория вероятностей в примерах