Felis


Начинающий
|
     
Спасибо, Old!
|
Всего сообщений: 71 | Присоединился: декабрь 2008 | Отправлено: 9 янв. 2009 0:11 | IP
|
|
aly17

Участник
|
     
Не знаю, в какой раздел кинуть это задание...решила сюда..)))
Найти значения параметра  , при котором функция , при котором функция =a\sin{x}+\ln{(1+3x)}) имеет экстремум в точке имеет экстремум в точке 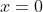 . Будет это максимум или минимум? . Будет это максимум или минимум?
(Сообщение отредактировал attention 6 дек. 2009 23:32)
|
Всего сообщений: 107 | Присоединился: декабрь 2008 | Отправлено: 11 янв. 2009 13:22 | IP
|
|
RKI 


Долгожитель
|
     
f(x) = asinx+ln(1+3x)
f'(x) = acosx + 3/(1+3x)
x=0 - точка экстремума => f'(0)=0
f'(0) = a+3 = 0
a=-3
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 11 янв. 2009 13:36 | IP
|
|
aly17

Участник
|
     
блин,точно.....оказывается лёгкий пример..))))спасибо большое!)))
|
Всего сообщений: 107 | Присоединился: декабрь 2008 | Отправлено: 11 янв. 2009 13:57 | IP
|
|
aly17

Участник
|
     
и ещё одно)))))))))))
Исследовать функцию на непрерывность:
 = \begin{cases} \frac{1}{x^2-4}, & \mbox{if} \quad x \leqslant 0 \\ 1-x, & \mbox{if} \quad 0 <x < 1 \\ \ln{x}, & \mbox{if} \quad x \geqslant 1\end{cases})
Выяснить существование и непрерывность f'(x)
(Сообщение отредактировал attention 6 дек. 2009 23:34)
|
Всего сообщений: 107 | Присоединился: декабрь 2008 | Отправлено: 11 янв. 2009 14:01 | IP
|
|
aly17

Участник
|
     
то есть,если пределы слева и справа равны,ф-я непрерывна??
|
Всего сообщений: 107 | Присоединился: декабрь 2008 | Отправлено: 11 янв. 2009 14:35 | IP
|
|
RKI 


Долгожитель
|
     
Далее необходимо исследовать производную на существование в точке x=1
И исследовать производную на непрерывность.
Делается по уже расписанному алгоритму.
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 11 янв. 2009 14:39 | IP
|
|
aly17

Участник
|
     
спасибо огромедное)))))))))))))))))))очень помогли!!)))))))
|
Всего сообщений: 107 | Присоединился: декабрь 2008 | Отправлено: 11 янв. 2009 14:41 | IP
|
|
Krolik

Новичок
|
      
Прошу прощения, если не там создаю сообщение (первый раз).
Непосредственно по определению можно доказать, что производная от четной (нечетной)
функции есть нечетная (четная) функция. Можно на основании этого свойства доказать, что если при интегрировании получается четная (нечетная) функция, то подынтегральная функция нечетная (четная). Однако, обратное утверждение мне доказать пока не удается, хотя подозреваю, что оно верно, т.к. не удается подобрать контрпримеров.
Вопрос: верно ли утверждение: «При интегрировании четной (нечетной) функции, выбирая из множества первообразных функцию с нужной (быть может, нулевой константой) всегда получается нечетная (четная) функция. »
Если утверждение верно, то буду весьма признателен хотя бы за схему доказательства, а если неверно, то за приведение контрпримера. Несмотря на поиски в классических учебниках, я почему-то не нашел освещение этого несложного вопроса, что ставит меня полностью в тупик.
|
Всего сообщений: 14 | Присоединился: январь 2009 | Отправлено: 13 янв. 2009 17:06 | IP
|
|
ProstoVasya

Долгожитель
|
     
Т.к. речь идёт о чётных и нечётных функциях, то области определения этих функций (для простоты) будем считать совпадающими со всей вещественной осью. Рассмотрите определённый интеграл с переменным верхним пределом и нижним пределом ноль. Этот интеграл (по теореме Барроу) является первообразной. Эта первообразная то, что Вам нужно. При доказательстве используйте теорему о замене переменной в определённом интеграле.
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 13 янв. 2009 19:20 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.1.4 Исследование функций одной и многих переменных
2.1.4 Исследование функций одной и многих переменных

 Форум
Форум

 Математика
Математика

 2.1.4 Исследование функций одной и многих переменных
2.1.4 Исследование функций одной и многих переменных