dima slayer
Новичок
|
    
СПАсибо!
|
Всего сообщений: 20 | Присоединился: март 2009 | Отправлено: 9 дек. 2009 22:07 | IP
|
|
attention 
Долгожитель
|
Для blond134
} {4x^2} = \mathop {\lim }\limits_{x \to 0} \left[\frac{\sin^2x}{4x^2} + \cos^2x\frac{\sin^2\frac{x}{2} }{2x^2} \right] = \hfill \\ = \frac{1}{4}\mathop {\lim }\limits_{x \to 0} {\left(\frac{\sin x}{x} \right)^2} + \frac{1}{8}\mathop {\lim }\limits_{x \to 0} {\cos ^2}x\mathop {\lim }\limits_{x \to 0} {\left( {\frac{\sin \frac{x}{2} }{\frac{x}{2} } } \right)^2} = \hfill \\ = \frac{1}{4} \cdot 1^2 + \frac{1}{8} \cdot 1^2 \cdot 1^2 = \frac{1}{4} + \frac{1}{8} = \frac{3}{8}. \hfill \\ \end{gathered})
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 10 дек. 2009 0:34 | IP
|
|
Grits
Новичок
|
Помогите, пожалуйста, решить предел:
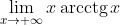
(Сообщение отредактировал attention 11 дек. 2009 5:50)
|
Всего сообщений: 3 | Присоединился: декабрь 2009 | Отправлено: 11 дек. 2009 5:41 | IP
|
|
attention
Долгожитель
|
Цитата: Grits написал 11 дек. 2009 4:41
Помогите пожалуйста решить предел :
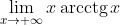
Grits, замените x на ctg(t), дальше все элементарно:
 = \hfill \\ = \mathop {\lim }\limits_{t \to 0} t\,\text{ctg}\,t = {\left(\mathop {\lim }\limits_{t \to 0} \frac{\sin t}{t}\right)^{-1} \cdot \mathop {\lim }\limits_{t \to 0} \cos t = 1^ {-1} \cdot 1 = 1. \hfill \\ \end{gathered})
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 11 дек. 2009 6:49 | IP
|
|
Grits
Новичок
|
спасибо огромное) ,и еще немогли бы в помочь мне еще с 1им пределом
помочь нужно с тем где корень кубический из x+1 - корень кубический из Х ))
(Сообщение отредактировал attention 11 дек. 2009 17:53)
|
Всего сообщений: 3 | Присоединился: декабрь 2009 | Отправлено: 11 дек. 2009 17:20 | IP
|
|
Veselo
Новичок
|
Собственно, задание - вычислить предел.
lim->Pi/3 (sin(x-Pi/3))/(1-2cos(x))
Я решал с помощью Лопиталя.
производная числителя: cos(x-Pi/3)
знаменателя: 3^1/2(корень из 3)
подставил - получилось 1/(3^1/2).
прошу развеять мои сомнения! =)
ps лучше решить через 1ый замечательный, но не получается у меня.
И ещё один.
Решить, применяя логарифмическое дифференцирование..
y=ctg(x)^5e^x
(катангенс x в степени 5e в степени x)
Очень прошу помочь мне, хочется разобраться.
И пожалуйста, пишите как можно подробнее, с комментариями. Хочется не просто слямзить ответ, а разобраться!
Спасибо.
|
Всего сообщений: 3 | Присоединился: декабрь 2009 | Отправлено: 11 дек. 2009 18:14 | IP
|
|
attention
Долгожитель
|
Цитата: Grits написал 11 дек. 2009 16:20
спасибо огромное) ,и еще немогли бы в помочь мне еще с 1им пределом
помочь нужно с тем где корень кубический из x+1 - корень кубический из Х ))
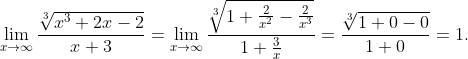
 = \hfill \\ = \mathop {\lim }\limits_{x \to \infty } \frac{\left(\sqrt[3]{x + 1} - \sqrt[3]{x}\right)\left(\sqrt[3]{(x + 1)^2} + \sqrt[3]{x^2 + x} + \sqrt[3]{x^2} \right)}{\sqrt[3]{(x + 1)^2} + \sqrt[3]{x^2 + x} + \sqrt[3]{x^2} } = \hfill \\ = \mathop {\lim }\limits_{x \to \infty } \frac{(x + 1) - x}{\sqrt[3]{(x + 1)^2} + \sqrt[3]{x^2 + x} + \sqrt[3]{x^2} } = \hfill \\ \mathop {\lim }\limits_{x \to \infty } \frac{1}{\sqrt[3]{(x + 1)^2} + \sqrt[3]{x^2 + x} + \sqrt[3]{x^2} } = 0. \hfill \\ \end{gathered} )
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 11 дек. 2009 19:18 | IP
|
|
2olegend
Новичок
|
Veselo
Ответ верный
Делаем замену: t=x-pi/3, x=t+pi/3, t->0
lim(x->0) (sin t)/(1-2cos(t+pi/3))=
=lim(x->0) (sin t)/(1-2*(cos(t) * cos(pi/3)-sin(t)*sin(pi/3)))=
=lim (x->0) (sin t)/(1-cos t+((3)^0.5)*sin t)=
{(1-cos t) эквив. (0.5*t^2) (t->0)}=
=(sin t)/(0.5*t^2+((3)^0.5)*sin t)=
{sin t экв. t (t->0)}=t/(0.5*t^2+((3)^0.5)*sin t)=
{сокращаем t в числ. и знамен. и подставляем t=0}=
=1/(0+(3)^0.5)=1/(корень из 3)
Grits
lim(x->oo) ((x+1)^(1/3)-x^(1/3))=
{домножаем и делим на ((x+1)^(2*1/3)+(x*(x+1))^(1/3)+x^(2*1/3)))}=lim(x->oo) (x+1-x)/(((x+1)^(2*1/3)+(x*(x+1))^(1/3)+x^(2*1/3))))=
{делим все слагаемые дроби на x^(2*1/3)}=
=lim(x->oo) (1/(x^(2*1/3)))/(1^(2*1/3)+1^(2*1/3)+1^(2*1/3))=
=0/3=0
(Сообщение отредактировал attention 11 дек. 2009 23:07)
(Сообщение отредактировал 2olegend 13 дек. 2009 13:02)
|
Всего сообщений: 16 | Присоединился: декабрь 2009 | Отправлено: 11 дек. 2009 20:53 | IP
|
|
Veselo
Новичок
|
Цитата: 2olegend написал 11 дек. 2009 22:59
Прошу прощения, свой предел уже нашел)
Можете проверить еще вот какой предел:
lim(x->0) (1/(sin x)^2-1/(x)^2) = 1/4
Маткад с вами согласен.
и спасибо большое за решение!
2ой бы пример как-то решить..=)
(Сообщение отредактировал attention 12 дек. 2009 17:14)
|
Всего сообщений: 3 | Присоединился: декабрь 2009 | Отправлено: 11 дек. 2009 23:02 | IP
|
|
2olegend
Новичок
|
А что решить то надо во втором? Просто производную найти или что?
Если производную, то лови:
/y=u^v, тогда y'=(u^v)*(v'*ln(u)+v*(u'/u))/ - вычисление производной показательно-степенной функции, применяя прием логарифмического дифференцирования. Соответственно, получим:
y'=(ctg(x)^5e^x)*((5e^x)*ln(ctg(x))+(5e^x)*(-1/(sin(x))^2)/ctg(x))
Упростить сможете сами)
(Сообщение отредактировал attention 12 дек. 2009 17:14)
|
Всего сообщений: 16 | Присоединился: декабрь 2009 | Отправлено: 12 дек. 2009 12:35 | IP
|
|
Форум
2.1.2 Предел функции одного и многих действ. аргументов
