RKI 


Долгожитель
|
     
Цитата: Guchi написал 22 янв. 2009 7:11
3. Даны координаты вершин пирамиды А1А2А3А4: А1(-2,3,-2), А2(2,-3,2), А3(2,2,0), А4(1,5,5) Сделать чертеж и найти:
3)уравнение прямой А1А2;
(x+2)/(2+2) = (y-3)/(-3-3) = (z+2)/(2+2)
(x+2)/4 = (y-3)/(-6) = (z+2)/4
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 22 янв. 2009 10:58 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Guchi написал 22 янв. 2009 7:11
3. Даны координаты вершин пирамиды А1А2А3А4: А1(-2,3,-2), А2(2,-3,2), А3(2,2,0), А4(1,5,5) Сделать чертеж и найти:
4)уравнение плоскости А1А2А3;
|x+2 y-3 z+2| = 0
| 4 -6 4 |
| 4 -1 2 |
(x+2)*|-6 4| - (y-3)*|4 4| + (z+2)*|4 -6| = 0
|-1 2| |4 2| |4 -1|
(x+2)*(-12+4) - (y-3)*(8-16) + (z+2)*(-4+24) = 0
-8*(x+2) + 8*(y-3) + 20*(z+2) = 0
-2*(x+2) + 2*(y-3) + 5*(z+2) = 0
-2x - 4 + 2y - 6 + 5z + 10 = 0
-2x + 2y + 5z = 0
2x - 2y - 5z = 0
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 22 янв. 2009 11:11 | IP
|
|
Vitkov

Новичок
|
      
Здравствуйте! Помогите, пожалуйста, с проблемой!
Исходные данные: я имею 3 точки в пространстве 1(x1,y1,z1), 2(x2,y2,z2) и 3(x3,y3,z3), c помощью которых необходимо задать плоскость (а именно плоский прямоугольник произвольно расположенный в пространстве).
Необходимо: определить координаты 4-ой точки 4(x4,y4,z4) с учетом, что задавался прямоугольник.
Спасибо!
|
Всего сообщений: 2 | Присоединился: январь 2009 | Отправлено: 22 янв. 2009 20:18 | IP
|
|
Melissa


Новичок
|
      
ужасная не решаемая задача!
если у кого-нибудь получиться - то видимо это страшно умный человек!
в равнобедренном треугольнике известны: уравнение основания х-2у+3=0; уравнение одной из боковых сторон 4х+у+5=0; точка 6/5; 28/5 на другой боковой стороне. Найти расстояние боковой стороны от противолежащей вершины.
|
Всего сообщений: 1 | Присоединился: октябрь 2009 | Отправлено: 23 окт. 2009 0:49 | IP
|
|
Legenda

Новичок
|
     
Помогите, пожалуйста, решить или хотябы найти формулы с обьяснениями к следуйщей задаче:
Даны координаты вершин тетраэдра А1(2;2;5), А2(2;5;1), А3(1;4;2), А4(0;1;4). Найти:
1) длину ребра А1,А2;
2) угол между ребрами А1,А2 и А1,А3;
3) площадь грани А1,А2,А3;
4) обьем тетраэдра;
5) увавнение медианы А1 треугольника А1,А2,А3;
6) уравнение грани А1,А2,А3;
7) уравнение высоты тетраэдра А4D, опущеной из вершины А4 на грань А1,А2,А3;
8) длину высоты (двумя способами).
|
Всего сообщений: 22 | Присоединился: октябрь 2009 | Отправлено: 25 окт. 2009 10:34 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Legenda написал 25 окт. 2009 10:34
Даны координаты вершин тетраэдра А1(2;2;5), А2(2;5;1), А3(1;4;2), А4(0;1;4). Найти:
1) длину ребра А1,А2;
 )
 )
^{2} + (5-2)^{2} + (1-5)^{2} } = )
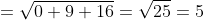
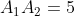
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 25 окт. 2009 12:16 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Legenda написал 25 окт. 2009 10:34
Даны координаты вершин тетраэдра А1(2;2;5), А2(2;5;1), А3(1;4;2), А4(0;1;4). Найти:
2) угол между ребрами А1,А2 и А1,А3;
 )
 )
 )
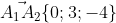
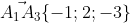
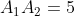
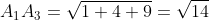
 = A_{1}A_{2}*A_{1}A_{3}*cos(A_{2}A_{1}A_{3}) = )
 )
 = 0*(-1) + 3*2 + (-4)*(-3) = 6 + 12 = 18 )
 = 18 )
 = \frac{18}{5\sqrt{14} } )
 )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 25 окт. 2009 12:25 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Legenda написал 25 окт. 2009 10:34
Даны координаты вершин тетраэдра А1(2;2;5), А2(2;5;1), А3(1;4;2), А4(0;1;4). Найти:
3) площадь грани А1,А2,А3;
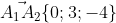
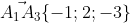
A1A2 x A1A3 = | i j k| = i*|3 -4| - j*| 0 -4| + k*|0 3| =
| 0 3 -4| |2 -3| |-1 -3| |-1 2|
|-1 2 -3|
= i*(-9 + 8) - j*(0 - 4) + k*(0 + 3) = - i + 4j + 3k
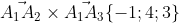
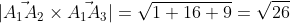
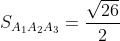
(Сообщение отредактировал RKI 25 окт. 2009 12:37)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 25 окт. 2009 12:36 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Legenda написал 25 окт. 2009 10:34
Даны координаты вершин тетраэдра А1(2;2;5), А2(2;5;1), А3(1;4;2), А4(0;1;4). Найти:
4) обьем тетраэдра;
 )
 )
 )
 )
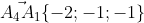
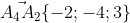
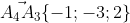
(A4A1; A4A2; A4A3) = |-2 -1 -1| =
|-2 -4 3|
|-1 -3 2|
= (-2)*|-4 3| - (-1)*|-2 3| + (-1)*|-2 -4| =
|-3 2| |-1 2| |-1 -3|
= (-2)*(-8 + 9) + 1*(-4 + 3) - 1*(6 - 4) = (-2)*1 + 1*(-1) - 1*2 =
= - 2 - 1 - 2 = -5
 | = |-5| = 5 )
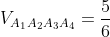
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 25 окт. 2009 12:52 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Legenda написал 25 окт. 2009 10:34
Даны координаты вершин тетраэдра А1(2;2;5), А2(2;5;1), А3(1;4;2), А4(0;1;4). Найти:
8) длину высоты (двумя способами).
1 способ
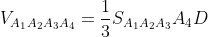
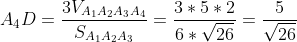
(Сообщение отредактировал RKI 25 окт. 2009 13:50)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 25 окт. 2009 13:48 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 Аналитическая геометрия
Аналитическая геометрия

 Форум
Форум

 Математика
Математика

 Аналитическая геометрия
Аналитическая геометрия