RKI 


Долгожитель
|
     
Цитата: vikycik написал 10 окт. 2009 1:54
2. Анализируется продолжительность телефонных разговоров с клиентами некоторой справочной телефонной службы. Случайным образом отобраны 60 телефонных разговоров и зафиксированы их длительности в секундах:
39 77 70 70 70 45 55 59 48 51
60 61 55 55 55 50 70 64 52 35
40 68 66 42 47 53 62 70 57 49
52 60 80 52 39 33 60 55 55 60
32 47 35 60 50 49 60 54 82 55
68 49 67 82 58 54 40 35 70 47
На базе этих данных:
1.постройте статистический ряд;
2.постройте эмпирическую функцию распределения и ее график;
3.постройте полигон частот;
4.постройте интервальный статистический ряд, включающий 5 подынтервалов;
5. на основе п.4 постройте гистограмму и по ее виду сформулируйте предположение о законе распределения рассматриваемой СВ;
6.постройте интервальный статистический ряд, включающий 7 подынтервалов;
7.на основании результатов пунктов1,4 и 6 вычислите выборочное среднее рассматриваемой СВ и сравните результаты вычислений.
2) эмпирическая функция
F(x) = {0, x <= 32
{1/60, 32 < x <= 33
{1/30, 33 < x <= 35
{1/12, 35 < x <= 39
{7/60, 39 < x <= 40
{3/20, 40 < x <= 42
{1/6, 42 < x <= 45
{11/60, 45 < x <= 47
{7/30, 47 < x <= 48
{1/4, 48 < x <= 49
{3/10, 49 < x <= 50
{1/3, 50 < x <= 51
{7/20, 51 < x <= 52
{2/5, 52 < x <= 53
{5/12, 53 < x <= 54
{9/20, 54 < x <= 55
{17/30, 55 < x <= 57
{7/12, 57 < x <= 58
{3/5, 58 < x <= 59
{37/60, 59 < x <= 60
{43/60, 60 < x <= 61
{11/15, 61 < x <= 62
{3/4, 62 < x <= 64
{23/30, 64 < x <= 66
{47/60, 66 < x <= 67
{4/5, 67 < x <= 68
{5/6, 68 < x <= 70
{14/15, 70 < x <= 77
{57/60, 77 < x <= 80
{29/30, 80 < x <= 82
{1, x > 82
График эмпирической функции будет иметь вид "лесенки"
3) полигон частот
Полигон частот - ломаная, отрезки которой соединяют точки (32, 1); (33, 1); (35, 3); (39, 2); (40, 2); (42, 1); (45, 1); (47, 3); (48, 1); (49, 3); (50, 2); (51, 1); (52, 3); (53, 1); (54, 2); (55, 7); (57, 1); (58, 1); (59, 1); (60, 6); (61, 1); (62, 1); (64, 1); (66, 1); (67, 1); (68, 2); (70, 6); (77, 1); (80, 1); (82, 2)
Полигон относительных частот - ломаная, отрезки которой соединяют точки (32, 1/60); (33, 1/60); (35, 1/20); (39, 1/30); (40, 1/30); (42, 1/60); (45, 1/60); (47, 1/20); (48, 1/60); (49, 1/20); (50, 1/30); (51, 1/60); (52, 1/20); (53, 1/60); (54, 1/30); (55, 7/60); (57, 1/60); (58, 1/60); (59, 1/60); (60, 1/10); (61, 1/60); (62, 1/60); (64, 1/60); (66, 1/60); (67, 1/60); (68, 1/30); (70, 1/10); (77, 1/60); (80, 1/60); (82, 1/30)
4) интервальный статистический ряд
k = 5 - количество интервалов
x(min) = 32
x(max) = 82
h - длина интервала
h = (x(max) - x(min))/k = (82-32)/5 = 10
x(i) - x(i+1) ni wi
32 - 42 10 1/6
42 - 52 14 7/30
52 - 62 21 7/20
62 - 72 11 11/60
72 - 82 4 1/15
5) гистограмма
Гистограмма относительных частот - ступенчатая фигура, состоящая из прямоугольников , основанием которых служат частичные интервалы (32, 42); (42, 52); (52, 62); (62, 72); (72, 82), а высоты равны соответственно 1/30; 7/150; 7/100; 11/300; 1/75
Площадь гистограммы равна 1
Если на гистограмме соединить середины верхних стороно прямоугольников, то полученная ломанная образует полигон относительных частот.
(Сообщение отредактировал attention 18 дек. 2009 18:53)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 12 окт. 2009 16:30 | IP
|
|
Tatiyaaaaa


Новичок
|
     
Здравствуйте! Помогите пожалуйста решить 3 задачи!!! Слёзно-слещно умоляю(
1. Для проверки качества поступившей партии зерна по схеме собственно-случайной бесповторной выборки произведено 10%-ное обследование. В результате анализа установлено следующее распределение данных о влажности зерна:
Процент влажности /менее 8/8–10/10–12/12–14/14–16/16–
–18/18–20/Более 20/Итого
Число проб 7/15/30/35/25/18/7/3/140
Найти: а) вероятность того, что средний процент влажности зерна в партии отличается от ее среднего процента в выборке не более чем на 0,5% (по абсолютной величине); б) границы, в которых с вероятностью 0,95 заключена доля зерна, влажность которого менее 12%; в) объем выборки, при которой те же границы для доли зерна, полученные в пункте б), можно гарантировать с вероятностью 0,9876; дать ответ на тот же вопрос, если никаких предварительных данных о рассматриваемой доле нет.
2. По данным задачи 1, используя -критерий Пирсона, на уровне значимости a = 0,05 проверить гипотезу о том, что случайная величина X – процент влажности зерна – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.
3. Распределение 60 предприятий по затратам рабочего времени X (тыс. человеко-дней (чел. дн.)) и выпуску продукции Y (млн. руб.) представлены в таблице:
y 30–40 /40–50/50–60/60–70/70–80/Итого:
x
10–25 1 3 2 6
25–40 3 6 4 1 14
40–55 3 7 6 1 17
55–70 1 6 4 4 15
70–85 2 5 1 8
Итого: 4 13 21 16 6 60
Необходимо:
1) Вычислить групповые средние , построить эмпирические линии регрессии;
2) Предполагая, что между переменными X и Y существует линейная корреляционная зависимость: а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений; б) вычислить коэффициент корреляции; на уровне значимости  = 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными X и Y; в) используя соответствующее уравнение регрессии, оценить средний выпуск продукции предприятия с затратами рабочего времени 55 тыс. чел. дн.
|
Всего сообщений: 4 | Присоединился: октябрь 2009 | Отправлено: 12 окт. 2009 17:20 | IP
|
|
Adrammelech


Новичок
|
     
Требуется помощь с последним пунктом.
Заранее спасибо.
В результате эксперимента получены данные, записанные в
виде статистического ряда. Требуется:
а) найти размах варьирования и построить интервальный
вариационный ряд;
б) построить полигон частот, гистограмму относительных
частот;
в) вычислить эмпирическую функцию распределения и
построить ее график;
г) найти числовые характеристики выборки
_
x(в), D(в), d(в), S^2, S
д) считая выборку соответствующей нормальному
распределению, найти доверительные интервалы для
математического ожидания при надежности y = 0,95;
е) приняв в качестве нулевой гипотезу H(0):генеральная
совокупность, из которой извлечена выборка, имеет нормальное распределение, проверить ее, пользуясь критерием Пирсона при
уровне значимости a = 0,05.
10,5 11,5 7,5 15,5 13,5 9,5 12 4,5 12,5 5,5
6,5 14,5 11,5 19,5 12 18 8 16 14,5 10
10,5 16,5 4 17,5 8,5 13 20,5 14 6 12,5
5,5 12 7,5 16 13,5 7,5 18,5 9,5 15,5 20
20,5 14,5 10 10 5,5 3,5 16,5 12,5 8 6
2,1 3,2 0,9 2,8 4,2 2,8 1,9 1,2 1,7 3,5
2,7 3,9 2,4 1,7 3,6 2,5 0,8 3,1 2,1 1,3
3,2 1,6 0,7 2,6 1,3 2 3,7 2,9 4 3,1
2,8 4,1 1,9 3,6 3,3 2,9 0,6 1,5 1,2 2,4
1,1 3,5 1,6 2,4 3,9 2,7 2,5 1,9 2,6 3,2
Из генеральной совокупности извлечена выборка объемом n .
Результаты измерения признаков X и Y выборки приведены в
корреляционной таблице. Найти:
а) числовые характеристики выборки;
б) уравнение линейной регрессии y на x .
в) выборочный коэффициент корреляции;
г) при уровне значимости а = 0,01 проверить нулевую гипотезу H(0):r(ген) о равенстве нулю генерального коэффициента корреляции.
X\Y 25200 25350 25500 25650 25800 25950 26100 26250 n(x)
3150 3 4 2 # # # # # 9
3200 # 5 7 5 # # # # 17
3250 # # # 8 14 6 # # 28
3300 # # # 6 8 9 # # 23
3350 # # # # # 5 6 3 14
3400 # # # # # # 5 4 9
n(y) 3 9 9 19 22 20 11 7 100
Заранее огромное спасибо!
(Сообщение отредактировал attention 18 дек. 2009 18:54)
|
Всего сообщений: 21 | Присоединился: сентябрь 2009 | Отправлено: 12 окт. 2009 17:33 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: vikycik написал 10 окт. 2009 1:54
2. Анализируется продолжительность телефонных разговоров с клиентами некоторой справочной телефонной службы. Случайным образом отобраны 60 телефонных разговоров и зафиксированы их длительности в секундах:
39 77 70 70 70 45 55 59 48 51
60 61 55 55 55 50 70 64 52 35
40 68 66 42 47 53 62 70 57 49
52 60 80 52 39 33 60 55 55 60
32 47 35 60 50 49 60 54 82 55
68 49 67 82 58 54 40 35 70 47
На базе этих данных:
1.постройте статистический ряд;
2.постройте эмпирическую функцию распределения и ее график;
3.постройте полигон частот;
4.постройте интервальный статистический ряд, включающий 5 подынтервалов;
5. на основе п.4 постройте гистограмму и по ее виду сформулируйте предположение о законе распределения рассматриваемой СВ;
6.постройте интервальный статистический ряд, включающий 7 подынтервалов;
7.на основании результатов пунктов1,4 и 6 вычислите выборочное среднее рассматриваемой СВ и сравните результаты вычислений.
6) интервальный статистический ряд
k = 7 - количество интервалов
x(min) = 32
x(max) = 82
h - длина интервала
h = (x(max) - x(min))/k = (82-32)/7 ~ 50/7
x(i) - x(i+1) ni wi
32 - 274/7 7 7/60
274/7 - 324/7 4 1/15
324/7 - 374/7 14 7/30
374/7 - 424/7 18 3/10
424/7 - 474/7 5 1/12
474/7 - 524/7 8 2/15
524/7 - 82 4 1/15
Цитата: vikycik написал 10 окт. 2009 1:54
2. Анализируется продолжительность телефонных разговоров с клиентами некоторой справочной телефонной службы. Случайным образом отобраны 60 телефонных разговоров и зафиксированы их длительности в секундах:
39 77 70 70 70 45 55 59 48 51
60 61 55 55 55 50 70 64 52 35
40 68 66 42 47 53 62 70 57 49
52 60 80 52 39 33 60 55 55 60
32 47 35 60 50 49 60 54 82 55
68 49 67 82 58 54 40 35 70 47
На базе этих данных:
1.постройте статистический ряд;
2.постройте эмпирическую функцию распределения и ее график;
3.постройте полигон частот;
4.постройте интервальный статистический ряд, включающий 5 подынтервалов;
5. на основе п.4 постройте гистограмму и по ее виду сформулируйте предположение о законе распределения рассматриваемой СВ;
6.постройте интервальный статистический ряд, включающий 7 подынтервалов;
7.на основании результатов пунктов1,4 и 6 вычислите выборочное среднее рассматриваемой СВ и сравните результаты вычислений.
7) выборочное среднее
ПО ПУНКТУ 1
x* = (32*1 + 33*1 + 35*3 + 39*2 + 40*2 + 42*1 + 45*1 + 47*3 + 48*1 + 49*3 + 50*2 + 51*1 + 52*3 + 53*1 + 54*2 + 55*7 + 57*1 + 58*1 + 59*1 + 60*6 + 61*1 + 62*1 + 64*1 + 66*1 + 67*1 + 68*2 + 70*6 + 77*1 + 80*1 + 82*2)/60 =
= (32 + 33 + 105 + 78 + 80 + 42 + 45 + 141 + 48 + 147 + 100 + 51 + 156 + 53 + 108 + 385 + 57 + 58 + 59 + 360 + 61 + 62 + 64 + 66 + 67 + 136 + 420 + 77 + 80 + 164)/60 =
= 3335/60 = 667/12 ~ 55.58
ПО ПУНКТУ 4
yi = (x(i) + x(i+1))/2
x(i) - x(i+1) ni yi
32 - 42 10 37
42 - 52 14 47
52 - 62 21 57
62 - 72 11 67
72 - 82 4 77
x* = (37*10 + 47*14 + 57*21 + 67*11 + 77*4)/60 =
= (370 + 658 + 1197 + 737 + 308)/60 = 3270/60 = 54.5
ПО ПУНКТУ 6
x(i) - x(i+1) ni yi
32 - 274/7 7 249/7
274/7 - 324/7 4 299/7
324/7 - 374/7 14 349/7
374/7 - 424/7 18 399/7
424/7 - 474/7 5 449/7
474/7 - 524/7 8 499/7
524/7 - 82 4 549/7
x* = (7*(249/7) + 4*(299/7) + 14*(349/7) + 18*(399/7) + 5*(449/7) + 8*(499/7) + 4*(549/7))/60 =
= (1743 + 1196 + 4886 + 7182 + 2245 + 3992 + 2196)/420 =
= 23440/420 = 1172/21 ~ 55.81
Цитата: vikycik написал 10 окт. 2009 1:54
3. Цена некоторого товара в двадцати магазинах была следующей:
50 47 50 50 48 52 50 50 50 50
48 55 45 52 50 48 47 48 52 48
На базе этих данных:
1.постройте статистический ряд;
2.постройте полигон относительных частот;
3.постройте эмпирическую функцию распределения и ее график;
4.постройте интервальный статистический ряд;
5.постройте гистограмму и по ее виду сформулируйте предположение о законе распределения рассматриваемой СВ;
1) статистический ряд
n = 20
wi = ni/n
xi ni wi
45 1 0.05
47 2 0.1
48 5 0.25
50 8 0.4
52 3 0.15
55 1 0.05
2) полигон относительных частот
Полигон относительных частот - ломаная, отрезки которой соединяют точки (45; 1); (47; 2); (48; 5); (50; 8); (52; 3); (55; 1).
3) эмпирическая функция распределения
F(x) = {0, x <= 45
{0.05, 45 < x <= 47
{0.15, 47 < x <= 48
{0.4, 48 < x <= 50
{0.8, 50 < x <= 52
{0.95, 52 < x <= 55
{1, x > 55
4) интервальный статистический ряд
x(min) = 45
x(max) = 55
k = 1 + log_{2} 20 ~ 1 + 4.322 ~ 5.322
k = 5
h = (x(max) - x(min))/k = (55-45)/5 = 2
x(i) - x(i+1) ni wi
45 - 47 3 0.15
47 - 49 5 0.25
49 - 51 8 0.4
51 - 53 3 0.15
53 - 55 1 0.05
5) гистограмма
Гистограмма относительных частот - ступенчатая фигура, состоящая из прямоугольников , основанием которых служат частичные интервалы (45, 47); (47, 49); (49, 51); (51, 53); (53, 55), а высоты равны соответственно 0.075; 0.125; 0.2; 0.075; 0.025
Цитата: vikycik написал 10 окт. 2009 1:54
4. По имеющейся эмпирической функции распределения постройте статистический ряд и полигон частот при условии, что объем выборки составляет 100 данных.
F(x)={0, x<=0
{0,2, 10< x<=20
{0,5, 20< x<=30
{0,65, 30< x<=40
{0,9, 40< x<=50
{0,95, 50< x<=60
{1, x>60
xi wi ni = n*wi = 100*wi
10 0.2 20
20 0.3 30
30 0.15 15
40 0.25 25
50 0.05 5
60 0.05 5
Полигон частот - ломаная, отрезки которой соединяют точки
(10;20); (20;30); (30;15); (40;25); (50;5); (60;5)
Полигон относительных частот - ломаная, отрезки которой соединяют точки (10; 0.2); (20; 0.3); (30; 0.15); (40; 0.25); (50; 0.05); (60; 0.05)
(Сообщение отредактировал attention 18 дек. 2009 18:55)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 12 окт. 2009 18:17 | IP
|
|
vikycik

Новичок
|
     
А почему 2 полигона в 4 задании? Какой из них правильный?
А как в 5 строит гистограмму и график накопленных частот?
(Сообщение отредактировал attention 18 дек. 2009 18:56)
|
Всего сообщений: 34 | Присоединился: сентябрь 2009 | Отправлено: 13 окт. 2009 1:45 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: vikycik написал 13 окт. 2009 1:45
А почему 2 полигона в 4 задании?какой из них правильный?
В математической статистике существует и полигон частот, и полигон относительных частот. Оба они правильные. Какой нужен Вам - уточните у преподавателя
Цитата: vikycik написал 10 окт. 2009 1:54
5. Проведено исследование посещаемости популярного интернет-сайта. В течение многих часов регистрируется число посетивших сайт в течение данного часа. Результаты исследования представлены в таблице.
Число посетителей 0 1 2 3 4 5 6
Количество часов 57 203 383 525 532 408 273
Число посетителей 7 8 9 10 11 12 13
Количество часов 139 45 27 10 4 1 1
Постройте гистограмму и график накопленных частот.
n = 57 + 203 + 383 + 525 + 532 + 408 + 273 + 139 + 45 + 27 + 10 + 4 + 1 + 1 = 2608
h = 1
wi = ni/n
xi ni wi = wi/h vi
0 57 57/2608 57/2608
1 203 203/2608 260/2608
2 383 383/2608 643/2608
3 525 525/2608 1168/2608
4 532 532/2608 1700/2608
5 408 408/2608 2108/2608
6 273 273/2608 2381/2608
7 139 139/2608 2520/2608
8 45 45/2608 2565/2608
9 27 27/2608 2592/2608
10 10 10/2608 2602/2608
11 4 4/2608 2606/2608
12 1 1/2608 2607/2608
13 1 1/2608 1
Гистограмма (относительных частот) - ступенчатая фигура, состоящая из прямоугольников, основанием которых служат частичные интервалы длиной h, а высоты равны wi/h.
Графиком накопленных частот называется фигура, строящаяся аналогично гистограмме, но для расчета высот берутся vi
(Сообщение отредактировал attention 18 дек. 2009 18:57)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 13 окт. 2009 9:39 | IP
|
|
vikycik

Новичок
|
     
Понятно.спасибо за помощь.
Нам дали только теоретический материал,а сами задачи не объясняли как решать.помогите еще решить пару задачек
3. Для отрасли, включающей 1200 фирм, составлена случайная выборка из 19 фирм. По выборке оказалось, что исправленное среднее квадратическое отклонение для числа работающих на фирме составляет s =25 (человек). Пользуясь 90%-ным доверительным интервалом, оцените среднее квадратическое отклонение для числа работающих на фирме по всей отрасли, построив доверительный интервал.
4. Найти минимальный объем выборки, при котором с надежностью 0,975 точность оценки математического ожидания а генеральной совокупности по выборочному среднему равна 0,3 , если известно среднее квадратическое отклонение =1,2, нормально распределенной генеральной совокупности.
5.Фирма коммунального хозяйства желает оценить на основе выборки среднюю квартплату за квартиры определенного типа с надежностью не менее 0,99 и погрешностью, меньше 10 ден. ед. Предполагая, что квартплата имеет нормальное распределение со средним квадратическое отклонением, не превышающим 35 ден. ед., найти минимальный объем выборки.
6.Для отрасли, включающей 1200 фирм, составлена случайная выборка из 19 фирм. По выборке оказалось, что в фирме в среднем работают x=77,5 человек при среднем квадратичном отклонении s=25 человек. Пользуясь 95%-ым доверительным интервалом, оценить среднее число работающих в фирме по всей отрасли и общее число работающих в отрасли. Предполагается, что количество работников фирмы имеет нормальное распределение.
7.Произведено 12 измерений одним прибором (без систематической ошибки) некоторой физической величины, причем исправленной среднее квадратическое отклонение случайных ошибок измерений оказалось равным 0,6. Найти точность прибора с надежностью 0,95. Предполагается, что результаты измерений распределены нормально.
8.По выборке из 25 упаковок товара средний вес составил 101 г с исправленным средним квадратическим отклонением 3 г. Построить доверительные интервалы для среднего и дисперсии с вероятностью 90%.
9.Производитель автомобильных шин заинтересован в получении оценки средней износоустойчивости шин особой модели. Он произвел случайную выборку объемом 10 шин и подверг их специальному испытанию. Средняя износоустойчивость, по данным выборки, оказалась равной 22500 миль с неисправленным средним квадратическим отклонением 3000 миль. Построить доверительный интервал с вероятностью 99% для средней износоустойчивости всего выпуска шин этого типа. Генеральная совокупность распределена нормально.
10.За последние 9 лет годовой рост цены актива А составлял в среднем 22% со средним квадратическим отклонением(исправленным) 6%. Построить доверительный интервал с вероятностью 90% для средней цены актива в конце следующего года, если в начале она была равна 200 ден. ед.
11.Бухгалтер компании решил предпринять выборочную проверку и выбрал 18 из 1200 компонент, продававшихся в прошлом месяце. Стоимость отборочных компонент 82; 30; 98; 116; 80; 150; 200; 88; 70; 90; 160; 100; 86; 76; 90; 140; 76; 68 (д.ед.). Найти оценку средней стоимости всех компонент и построить для нее доверительный интервал с надежностью 0,95. Какой объем выборки необходим для точности интервальной оценки =3 (ден. ед.)?
12.Данные о производстве зерна в России в 1996-2002 гг. представлены в таблице.
Год 1996 19971998 1999 2000 2001 2002
Производство,
млн т 69,3 88,647,9 54,7 65,5 85,286,6
Построить доверительные интервалы для среднего и для следующего наблюдения с надежностью 95%, использую нормальное приближение.
13.В таблице приведены сгруппированные данные о коэффициентах соотношения заемных и собственных средств на 100 малых предприятиях региона.
Номер Интервал Середина ni
интервала интервала
1 5,05-5,15 5,1 5
2 5,15-5,25 5,2 8
3 5,25-5,35 5,3 12
4 5,35-5,45 5,4 20
5 5,45-5,55 5,5 26
6 5,55-5,65 5,6 15
7 5,65-5,75 5,7 10
8 5,75-5,85 5,8 4
Построить доверительные интервалы для среднего и для следующего наблюдения с надежностью 95%, используя нормальное приближение.
(Сообщение отредактировал attention 18 дек. 2009 18:58)
|
Всего сообщений: 34 | Присоединился: сентябрь 2009 | Отправлено: 13 окт. 2009 13:40 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Tatiyaaaaa написал 12 окт. 2009 17:20
2. По данным задачи 1, используя -критерий Пирсона, на уровне значимости a = 0,05 проверить гипотезу о том, что случайная величина X – процент влажности зерна – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.
n = 140
ci = (x(i-1)+x(i))
x(i-1) - x(i) mi ci
< 8 7 7
8 - 10 15 9
10 - 12 30 11
12 - 14 35 13
14 - 16 25 15
16 - 18 18 17
18 - 20 7 19
> 20 3 21
x* = (7*7 + 9*15 + 11*30 + 13*35 + 15*25 + 17*18 + 19*7 + 21*3)/140 =
= (49 + 135 + 330 + 455 + 375 + 306 + 133 + 63)/140 =
= 1846/140
x* ~ 13.1857
s^2 = (1/140)(7*(7-13.1857)^2 + 15*(9-13.1857)^2 + 30*(11-13.1857)^2 + 35*(13-13.1857)^2 + 25*(15-13.1857)^2 + 18*(17-13.1857)^2 + 7*(19-13.1857)^2 + 3*(21-13.1857)^2) ~
~ (1/140)(267.8402 + 262.8013 + 143.3185 + 1.2070 + 82.2921 + 55.4938 + 236.6426 + 183.1899) ~ 8.80561
s ~ 2.9674
p1 = P(X < 7) ~ 0.5 + Ф((7-13.1857)/2.9674) ~
~ 0.5 + Ф(-2.08) = 0.5 - Ф(2.08) ~ 0.5 - 0.4812 = 0.0188
p2 = P(7 < X < 9) ~
~ Ф((9-13.1857)/2.9674) - Ф((7-13.1857)/2.9674) ~
~ Ф(-1.41) - Ф(-2.08) = - Ф(1.41) + Ф(2.08) ~
~ - 0.4207 + 0.4812 = 0.0605
p3 = P(9 < X < 11) ~
~ Ф((11-13.1857)/2.9674) - Ф((9-13.1857)/2.9674) ~
~ Ф(-0.74) - Ф(-1.41) = - Ф(0.74) + Ф(1.41) ~
~ - 0.2703 + 0.4207 = 0.1504
p4 = P(11 < X < 13) ~
~ Ф((13-13.1857)/2.9674) - Ф((11-13.1857)/2.9674) ~
~ Ф(-0.06) - Ф(-0.74) = - Ф(0.06) + Ф(0.74) ~
~ - 0.0239 + 0.2703 = 0.2464
p5 = P(13 < X <15) ~
~ Ф((15-13.1857)/2.9674) - Ф((13-13.1857)/2.9674) ~
~ Ф(0.61) - Ф(-0.06) = Ф(0.61) + Ф(0.06) ~
~ 0.2291 + 0.0239 = 0.253
p6 = P(15 < X < 17) ~
~ Ф((17-13.1857)/2.9674) - Ф((15-13.1857)/2.9674) ~
~ Ф(1.29) - Ф(0.61) ~ 0.4015 - 0.2291 = 0.1724
p7 = P(17 < X < 19) ~
~ Ф((19-13.1857)/2.9674) - Ф((17-13.1857)/2.9674) ~
~ Ф(1.96) - Ф(1.29) ~ 0.4750 - 0.4015 = 0.0735
p8 = P(X > 19) = 0.5 - Ф((19-13.1857)/2.9674) ~
~ 0.5 - Ф(1.96) ~ 0.5 - 0.4750 = 0.025
x(i-1) - x(i) mi pi npi mi - npi (mi-npi)^2/npi
< 8 7 0.0188 2.632 4.368 7.25
8 - 10 15 0.0605 8.47 6.53 5.03
10 - 12 30 0.1504 21.056 8.944 3.80
12 - 14 35 0.2464 34.496 0.504 0.01
14 - 16 25 0.253 35.42 -10.42 3.07
16 - 18 18 0.1724 24.136 -6.136 1.56
18 - 20 7 0.0735 10.29 -3.29 1.05
> 20 3 0.025 3.5 -0.5 0.07
хи-квадрат = 7.25 + 5.03 + 3.80 + 0.01 + 3.07 + 1.56 + 1.05 + 0.07 = 21.84
a = 0.05
число степеней свободы r-1-k = 8-1-2 = 5
критическая точка = 11.1
21.84 > 11.1
Случайная величина X НЕ распределена по нормальному закону
Цитата: vikycik написал 13 окт. 2009 13:57
3. Для отрасли, включающей 1200 фирм, составлена случайная выборка из 19 фирм. По выборке оказалось, что исправленное среднее квадратическое отклонение для числа работающих на фирме составляет s =25 (человек). Пользуясь 90%-ным доверительным интервалом, оцените среднее квадратическое отклонение для числа работающих на фирме по всей отрасли, построив доверительный интервал.
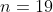
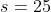

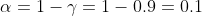
Необходимо оценить 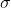
Найдем критические точки хи-квадрат распределения с n-1 = 19-1 = 18 степенями свободы и соответствующими уровнями значимости:
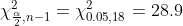
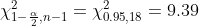
Тогда
s^2}{\chi^{2}_{\frac{\alpha}{2}, n-1} } < \sigma^{2} < \frac{(n-1)s^2}{\chi^{2}_{1 - \frac{\alpha}{2}, n-1} } )


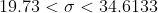
Цитата: vikycik написал 13 окт. 2009 13:57
4. Найти минимальный объем выборки, при котором с надежностью 0,975 точность оценки математического ожидания а генеральной совокупности по выборочному среднему равна 0,3 , если известно среднее квадратическое отклонение =1,2, нормально распределенной генеральной совокупности.
n - объем выборки

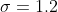
 = \frac{\gamma}{2} = \frac{0.975}{2} = 0.4875 )
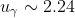
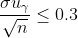

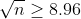
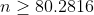
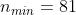
Цитата: vikycik написал 13 окт. 2009 13:57
5.Фирма коммунального хозяйства желает оценить на основе выборки среднюю квартплату за квартиры определенного типа с надежностью не менее 0,99 и погрешностью, меньше 10 ден. ед. Предполагая, что квартплата имеет нормальное распределение со средним квадратическое отклонением, не превышающим 35 ден. ед., найти минимальный объем выборки.
n - объем выборки
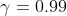
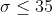
 = \frac{\gamma}{2} = \frac{0.99}{2} = 0.495 )
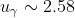
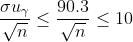
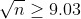
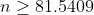

Цитата: vikycik написал 13 окт. 2009 13:57
6.Для отрасли, включающей 1200 фирм, составлена случайная выборка из 19 фирм. По выборке оказалось, что в фирме в среднем работают x=77,5 человек при среднем квадратичном отклонении s=25 человек. Пользуясь 95%-ым доверительным интервалом, оценить среднее число работающих в фирме по всей отрасли и общее число работающих в отрасли. Предполагается, что количество работников фирмы имеет нормальное распределение.
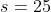
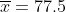
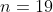
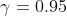
 - критическая точка распределения Стьюдента с n-1 = 19-1 = 18 степенями свободы на уровне значимости - критическая точка распределения Стьюдента с n-1 = 19-1 = 18 степенями свободы на уровне значимости

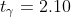
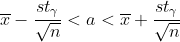
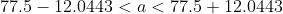
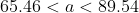

Цитата: vikycik написал 13 окт. 2009 13:57
7.Произведено 12 измерений одним прибором (без систематической ошибки) некоторой физической величины, причем исправленной среднее квадратическое отклонение случайных ошибок измерений оказалось равным 0,6. Найти точность прибора с надежностью 0,95. Предполагается, что результаты измерений распределены нормально.
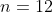

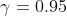

s^2}{\chi^{2}_{\frac{\alpha}{2}, n-1} } < \sigma^2 < \frac{(n-1)s^2}{\chi^{2}_{1 - \frac{\alpha}{2}, n-1} } )
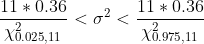
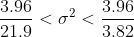
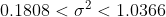

Цитата: vikycik написал 13 окт. 2009 13:57
8.По выборке из 25 упаковок товара средний вес составил 101 г с исправленным средним квадратическим отклонением 3 г. Построить доверительные интервалы для среднего и дисперсии с вероятностью 90%.

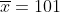
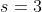

 - критическая точка распределения Стьюдента с n-1 = 25-1 = 24 степенями свободы на уровне значимости - критическая точка распределения Стьюдента с n-1 = 25-1 = 24 степенями свободы на уровне значимости
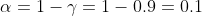
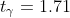
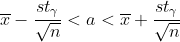
}{\sqrt{25} } < a < 101 + \frac{3*(1.71)}{\sqrt{25} } )
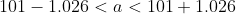

s^2}{\chi^{2}_{\frac{\alpha}{2}, n-1} } < \sigma^{2} < \frac{(n-1)s^2}{\chi^{2}_{1 - \frac{\alpha}{2}, n-1} } )
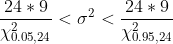
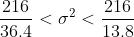
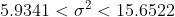
Цитата: vikycik написал 13 окт. 2009 13:57
10.За последние 9 лет годовой рост цены актива А составлял в среднем 22% со средним квадратическим отклонением(исправленным) 6%. Построить доверительный интервал с вероятностью 90% для средней цены актива в конце следующего года, если в начале она была равна 200 ден. ед.
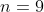
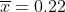
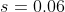

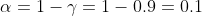

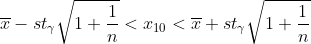
*(1.86)*(1.0541) < x_{10} < 0.22 + (0.06)*(1.86)*(1.0541) )
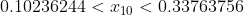
 < a < 200*(1.33763756) )
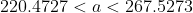
(Сообщение отредактировал attention 18 дек. 2009 19:05)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 13 окт. 2009 14:17 | IP
|
|
vikycik

Новичок
|
     
спасибо за помощь
|
Всего сообщений: 34 | Присоединился: сентябрь 2009 | Отправлено: 15 окт. 2009 1:47 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Adrammelech написал 12 окт. 2009 17:33
Требуется помощь с последним пунктом.
Заранее спасибо.
В результате эксперимента получены данные, записанные в
виде статистического ряда. Требуется:
а) найти размах варьирования и построить интервальный
вариационный ряд;
10,5 11,5 7,5 15,5 13,5 9,5 12 4,5 12,5 5,5
6,5 14,5 11,5 19,5 12 18 8 16 14,5 10
10,5 16,5 4 17,5 8,5 13 20,5 14 6 12,5
5,5 12 7,5 16 13,5 7,5 18,5 9,5 15,5 20
20,5 14,5 10 10 5,5 3,5 16,5 12,5 8 6
2,1 3,2 0,9 2,8 4,2 2,8 1,9 1,2 1,7 3,5
2,7 3,9 2,4 1,7 3,6 2,5 0,8 3,1 2,1 1,3
3,2 1,6 0,7 2,6 1,3 2 3,7 2,9 4 3,1
2,8 4,1 1,9 3,6 3,3 2,9 0,6 1,5 1,2 2,4
1,1 3,5 1,6 2,4 3,9 2,7 2,5 1,9 2,6 3,2
а)
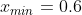
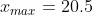
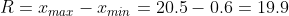

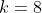
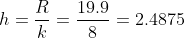
x(i-1) - x(i) ni
0.6 - 3.0875 34
3.0875 - 5.575 22
5.575 - 8.0625 8
8.0625 - 10.55 8
10.55 - 13.0375 9
13.0375 - 15.525 8
15.525 - 18.0125 6
18.0125 - 20.5 5
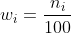
x(i-1) - x(i) ni wi
0.6 - 3.0875 34 0.34
3.0875 - 5.575 22 0.22
5.575 - 8.0625 8 0.08
8.0625 - 10.55 8 0.08
10.55 - 13.0375 9 0.09
13.0375 - 15.525 8 0.08
15.525 - 18.0125 6 0.06
18.0125 - 20.5 5 0.05
Цитата: Adrammelech написал 12 окт. 2009 17:33
Требуется помощь с последним пунктом.
Заранее спасибо.
В результате эксперимента получены данные, записанные в
виде статистического ряда. Требуется:
б) построить полигон частот, гистограмму относительных
частот;
10,5 11,5 7,5 15,5 13,5 9,5 12 4,5 12,5 5,5
6,5 14,5 11,5 19,5 12 18 8 16 14,5 10
10,5 16,5 4 17,5 8,5 13 20,5 14 6 12,5
5,5 12 7,5 16 13,5 7,5 18,5 9,5 15,5 20
20,5 14,5 10 10 5,5 3,5 16,5 12,5 8 6
2,1 3,2 0,9 2,8 4,2 2,8 1,9 1,2 1,7 3,5
2,7 3,9 2,4 1,7 3,6 2,5 0,8 3,1 2,1 1,3
3,2 1,6 0,7 2,6 1,3 2 3,7 2,9 4 3,1
2,8 4,1 1,9 3,6 3,3 2,9 0,6 1,5 1,2 2,4
1,1 3,5 1,6 2,4 3,9 2,7 2,5 1,9 2,6 3,2
б)
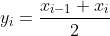
x(i-1) - x(i) ni wi yi
0.6 - 3.0875 34 0.34 1.84375
3.0875 - 5.575 22 0.22 4.33125
5.575 - 8.0625 8 0.08 6.81875
8.0625 - 10.55 8 0.08 9.30625
10.55 - 13.0375 9 0.09 11.79375
13.0375 - 15.525 8 0.08 14.28125
15.525 - 18.0125 6 0.06 16.76875
18.0125 - 20.5 5 0.05 19.25625
Полигон частот - ломаная отрезки которой соединяют точки  )
Гистограмма относительных частот - супенчатая фигура, состоящая из прямоугольников, основанием которых служат частичные интервалы  ) длиной h, а высоты равны длиной h, а высоты равны 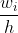
Цитата: Adrammelech написал 12 окт. 2009 17:33
Требуется помощь с последним пунктом.
Заранее спасибо.
В результате эксперимента получены данные, записанные в
виде статистического ряда. Требуется:
в) вычислить эмпирическую функцию распределения и
построить ее график;
10,5 11,5 7,5 15,5 13,5 9,5 12 4,5 12,5 5,5
6,5 14,5 11,5 19,5 12 18 8 16 14,5 10
10,5 16,5 4 17,5 8,5 13 20,5 14 6 12,5
5,5 12 7,5 16 13,5 7,5 18,5 9,5 15,5 20
20,5 14,5 10 10 5,5 3,5 16,5 12,5 8 6
2,1 3,2 0,9 2,8 4,2 2,8 1,9 1,2 1,7 3,5
2,7 3,9 2,4 1,7 3,6 2,5 0,8 3,1 2,1 1,3
3,2 1,6 0,7 2,6 1,3 2 3,7 2,9 4 3,1
2,8 4,1 1,9 3,6 3,3 2,9 0,6 1,5 1,2 2,4
1,1 3,5 1,6 2,4 3,9 2,7 2,5 1,9 2,6 3,2
в)
F(x) = {0, x <= 1.84375
{0.34, 1.84375 < x <= 4.33125
{0.56, 4.33125 < x <= 6.81875
{0.64, 6.81875 < x <= 9.30625
{0.72, 9.30625 < x <= 11.79375
{0.81, 11.79375 < x <= 14.28125
{0.89, 14.28125 < x <= 16.76875
{0.95, 16.76875 < x <= 19.25625
{1, x > 19.25625
Цитата: Adrammelech написал 12 окт. 2009 17:33
Требуется помощь с последним пунктом.
Заранее спасибо.
В результате эксперимента получены данные, записанные в
виде статистического ряда. Требуется:
г) найти числовые характеристики выборки
_
x(в), D(в), d(в), S^2, S
10,5 11,5 7,5 15,5 13,5 9,5 12 4,5 12,5 5,5
6,5 14,5 11,5 19,5 12 18 8 16 14,5 10
10,5 16,5 4 17,5 8,5 13 20,5 14 6 12,5
5,5 12 7,5 16 13,5 7,5 18,5 9,5 15,5 20
20,5 14,5 10 10 5,5 3,5 16,5 12,5 8 6
2,1 3,2 0,9 2,8 4,2 2,8 1,9 1,2 1,7 3,5
2,7 3,9 2,4 1,7 3,6 2,5 0,8 3,1 2,1 1,3
3,2 1,6 0,7 2,6 1,3 2 3,7 2,9 4 3,1
2,8 4,1 1,9 3,6 3,3 2,9 0,6 1,5 1,2 2,4
1,1 3,5 1,6 2,4 3,9 2,7 2,5 1,9 2,6 3,2
г)
*(1.84375) + (0.22)*(4.33125) + (0.08)*(6.81875) + )
*(9.30625) + (0.09)*(11.79375) + (0.08)*(14.28125) + )
*(16.76875) + (0.05)*(19.25625) = )


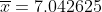
Цитата: Adrammelech написал 12 окт. 2009 17:33
Требуется помощь с последним пунктом.
Заранее спасибо.
В результате эксперимента получены данные, записанные в
виде статистического ряда. Требуется:
г) найти числовые характеристики выборки
_
x(в), D(в), d(в), S^2, S
10,5 11,5 7,5 15,5 13,5 9,5 12 4,5 12,5 5,5
6,5 14,5 11,5 19,5 12 18 8 16 14,5 10
10,5 16,5 4 17,5 8,5 13 20,5 14 6 12,5
5,5 12 7,5 16 13,5 7,5 18,5 9,5 15,5 20
20,5 14,5 10 10 5,5 3,5 16,5 12,5 8 6
2,1 3,2 0,9 2,8 4,2 2,8 1,9 1,2 1,7 3,5
2,7 3,9 2,4 1,7 3,6 2,5 0,8 3,1 2,1 1,3
3,2 1,6 0,7 2,6 1,3 2 3,7 2,9 4 3,1
2,8 4,1 1,9 3,6 3,3 2,9 0,6 1,5 1,2 2,4
1,1 3,5 1,6 2,4 3,9 2,7 2,5 1,9 2,6 3,2
*(1.84375 - 7.042625)^{2} + (0.22)*(4.33125 - 7.042625)^{2} + )
*(6.81875 - 7.042625)^{2} + (0.08)*(9.30625 - 7.042625)^{2} + )
*(11.79375 - 7.042625)^{2} + (0.08)*(14.28125 - 7.042625)^{2} + )
*(16.76875 - 7.042625)^{2} + (0.05)*(19.25625 - 7.042625)^{2} = )
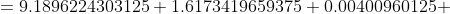
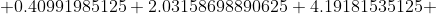
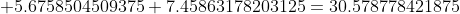
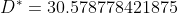
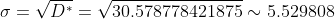

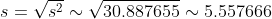
Цитата: Adrammelech написал 12 окт. 2009 17:33
В результате эксперимента получены данные, записанные в
виде статистического ряда. Требуется:
д) считая выборку соответствующей нормальному
распределению, найти доверительные интервалы для
математического ожидания при надежности y = 0,95;
10,5 11,5 7,5 15,5 13,5 9,5 12 4,5 12,5 5,5
6,5 14,5 11,5 19,5 12 18 8 16 14,5 10
10,5 16,5 4 17,5 8,5 13 20,5 14 6 12,5
5,5 12 7,5 16 13,5 7,5 18,5 9,5 15,5 20
20,5 14,5 10 10 5,5 3,5 16,5 12,5 8 6
2,1 3,2 0,9 2,8 4,2 2,8 1,9 1,2 1,7 3,5
2,7 3,9 2,4 1,7 3,6 2,5 0,8 3,1 2,1 1,3
3,2 1,6 0,7 2,6 1,3 2 3,7 2,9 4 3,1
2,8 4,1 1,9 3,6 3,3 2,9 0,6 1,5 1,2 2,4
1,1 3,5 1,6 2,4 3,9 2,7 2,5 1,9 2,6 3,2
1) для математического ожидания при известной дисперсии
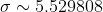
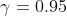
 = \frac{\gamma}{2} = \frac{0.95}{2} = 0.475 )
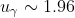

*(1.96)}{10} < a < 7.042625 + \frac{(5.529808)*(1.96)}{10} )
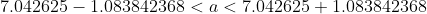
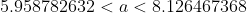
2) для математического ожидания при неизвестной дисперсии
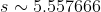

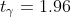
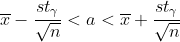
*(1.96)}{10} < a < 7.042625 + \frac{(5.557666)*(1.96)}{10} )
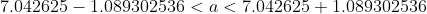
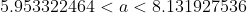
Цитата: Adrammelech написал 12 окт. 2009 17:33
В результате эксперимента получены данные, записанные в
виде статистического ряда. Требуется:
е) приняв в качестве нулевой гипотезу H(0):генеральная
совокупность, из которой извлечена выборка, имеет нормальное распределение, проверить ее, пользуясь критерием Пирсона при
уровне значимости a = 0,05.
10,5 11,5 7,5 15,5 13,5 9,5 12 4,5 12,5 5,5
6,5 14,5 11,5 19,5 12 18 8 16 14,5 10
10,5 16,5 4 17,5 8,5 13 20,5 14 6 12,5
5,5 12 7,5 16 13,5 7,5 18,5 9,5 15,5 20
20,5 14,5 10 10 5,5 3,5 16,5 12,5 8 6
2,1 3,2 0,9 2,8 4,2 2,8 1,9 1,2 1,7 3,5
2,7 3,9 2,4 1,7 3,6 2,5 0,8 3,1 2,1 1,3
3,2 1,6 0,7 2,6 1,3 2 3,7 2,9 4 3,1
2,8 4,1 1,9 3,6 3,3 2,9 0,6 1,5 1,2 2,4
1,1 3,5 1,6 2,4 3,9 2,7 2,5 1,9 2,6 3,2
x(i-1) - x(i) ni yi
0.6 - 3.0875 34 1.84375
3.0875 - 5.575 22 4.33125
5.575 - 8.0625 8 6.81875
8.0625 - 10.55 8 9.30625
10.55 - 13.0375 9 11.79375
13.0375 - 15.525 8 14.28125
15.525 - 18.0125 6 16.76875
18.0125 - 20.5 5 19.25625
 \sim )
 = 0.5 - \Phi (0.94) \sim 0.5 - 0.3264 = 0.1736 )
 - \Phi (\frac{1.84375 - 7.042625}{5.557666}) \sim )
 - \Phi (-0.94) = - \Phi (0.49) + \Phi (0.94) \sim )

 - \Phi (\frac{4.33125 - 7.042625}{5.557666}) \sim )
 - \Phi (-0.49) = - \Phi (0.04) + \Phi (0.49) \sim )

 - \Phi (\frac{6.81875 - 7.042625}{5.557666}) \sim )
 - \Phi (-0.04) = \Phi (0.41) + \Phi (0.04) \sim )

 - \Phi (\frac{9.30625 - 7.042625}{5.557666}) \sim )
 - \Phi (0.41) \sim 0.3023 - 0.1591 = 0.1432 )
 - \Phi (\frac{11.79375 - 7.042625}{5.557666}) \sim )
 - \Phi (0.85) \sim 0.4032 - 0.3023 = 0.1009 )
 - \Phi (\frac{14.28125 - 7.042625}{5.557666}) \sim )
 - \Phi (1.30) \sim 0.4599 - 0.4032 = 0.0567 )
 \sim 0.5 - 0.4599 = 0.0401 )
x(i-1) - x(i) ni pi npi ni - npi
0.6 - 3.0875 34 0.1736 17.36 16.64
3.0875 - 5.575 22 0.1385 13.85 8.15
5.575 - 8.0625 8 0.1719 17.19 -9.19
8.0625 - 10.55 8 0.1751 17.51 -9.51
10.55 - 13.0375 9 0.1432 14.32 -5.32
13.0375 - 15.525 8 0.1009 10.09 -2.09
15.525 - 18.0125 6 0.0567 5.67 0.33
18.0125 - 20.5 5 0.0401 4.01 0.99
x(i-1) - x(i) npi ni - npi (ni - npi)^2/npi
0.6 - 3.0875 17.36 16.64 15.95
3.0875 - 5.575 13.85 8.15 4.80
5.575 - 8.0625 17.19 -9.19 4.91
8.0625 - 10.55 17.51 -9.51 5.17
10.55 - 13.0375 14.32 -5.32 1.98
13.0375 - 15.525 10.09 -2.09 0.43
15.525 - 18.0125 5.67 0.33 0.02
18.0125 - 20.5 4.01 0.99 0.24
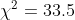
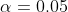

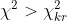
Следовательно, гипотеза не принимается
(Сообщение отредактировал attention 18 дек. 2009 19:11)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 15 окт. 2009 19:32 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 2.6.3 Математическая статистика
2.6.3 Математическая статистика

 Форум
Форум

 Математика
Математика

 2.6.3 Математическая статистика
2.6.3 Математическая статистика