ElarniA
Новичок
|
      
Людиииии...неужели никто не знает как решить эту задачку:
Найти стороны прямоугольника наибольшей площади, который можно вписать в эллипс х^2/25 + y^2/9 = 1
|
Всего сообщений: 12 | Присоединился: октябрь 2009 | Отправлено: 21 окт. 2009 13:39 | IP
|
|
ProstoVasya
Долгожитель
|
little fox
Если бы на ферме жили только кролики, то ног было 4000. Т.е. лишних ног 850. Поэтому 425 кроликов надо превратить в кур (оторвать у каждого лишнюю пару лап). Таким образом на ферме 425 кур и 575 кроликов.
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 21 окт. 2009 19:48 | IP
|
|
ProstoVasya
Долгожитель
|
ElarniA
Из соображений симметрии прямоугольник наибольшей площади будет иметь стороны параллельные осям координат. Достаточно вычислить площадь прямоугольника, расположенного в первой четверти, а потом умножить на 4. Пусть точка из первого квадранта лежит на эллипсе и имеет координаты (x,y). Тогда площадь прямоугольника равна
S = 4 x y. Возведём в квадрат, и будем искать максимум функции
S^2 = 16 x^2 y^2
Выражение для y^2 возьмём из уравнения эллипса. Тогда
S^2 = 16*9(x^2 - x^4/25)
Эта функция обращается в нуль при x=0 b x = 5.
Теперь, производную приравняем нулю и найдём точку экстремума
16*9(2x -4 x^3/25) = 0
Отсюда, x^2 = 25/2. Максимальная площадь равна S =30
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 21 окт. 2009 20:04 | IP
|
|
ElarniA
Новичок
|
ProstoVasya
Спасибо Вам большое!
|
Всего сообщений: 12 | Присоединился: октябрь 2009 | Отправлено: 22 окт. 2009 7:48 | IP
|
|
grobak
Новичок
|
-----------------Помощь студентам----------------------------------------
Решение заданий и контрольных по любым предметам, написание курсовых и дипломных.
внешняя ссылка удалена
мы вконтакте: внешняя ссылка удалена
|
Всего сообщений: 4 | Присоединился: октябрь 2009 | Отправлено: 22 окт. 2009 16:13 | IP
|
|
little_fox
Новичок
|
 
Спасибо, ProstoVasya!! *оторвать у каждого лишнюю пару лап* жесть ваще)))
(Сообщение отредактировал little fox 23 окт. 2009 16:48)
|
Всего сообщений: 16 | Присоединился: апрель 2009 | Отправлено: 23 окт. 2009 16:39 | IP
|
|
Krolik
Новичок
|
Вопрос по топологии
(Сообщение отредактировал Krolik 24 окт. 2009 15:15)
|
Всего сообщений: 14 | Присоединился: январь 2009 | Отправлено: 24 окт. 2009 15:13 | IP
|
|
hochyznatmatematiky
Новичок
|
Помогите решить уравнение 6X^4+5x^3-38x^2+5X+6=0 если можно с места, там где обратная замена поподробнее..заранее благодарю.
|
Всего сообщений: 1 | Присоединился: октябрь 2009 | Отправлено: 24 окт. 2009 23:25 | IP
|
|
RKI 
Долгожитель
|
Цитата: hochyznatmatematiky написал 24 окт. 2009 23:25
Помогите решить уравнение 6X^4+5x^3-38x^2+5X+6=0 если можно с места, там где обратная замена поподробнее..заранее благодарю.
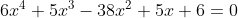
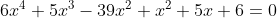
 + (x^{2} + 5x + 6) = 0 )
(x+3) + (x+2)(x+3) = 0 )
(x^{2} (6x-13) + x + 2) = 0 )
(6x^{3} - 13x^{2} + x + 2) = 0 )
(x-2)(6x^{2} - x - 1) = 0 )
(x-2)(x - \frac{1}{2})(x + \frac{1}{3}) = 0 )
|
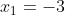
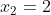
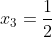
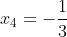
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 25 окт. 2009 16:34 | IP
|
|
ProstoVasya
Долгожитель
|
Krolik
К сожалению, я не профессионал в геометрии, но постараюсь ответить на Ваши вопросы. Возможно на форуме найдутся люди, кто это сделает лучше.
В первую очередь, S^n - n- мерная сфера. Поэтому S^2 - обычная сфера в трёхмерном пространстве, а S^3 в четырёхмерном.
Вы рисуете сферы S^2 и S^1. Правда, я сомневаюсь, что в этом случае есть непрерывное отображение отличное от постоянного. Это во многом снимает 6 вопрос.
На первые два вопроса - ответ: да, правильно.
3. Когда у Вас гладкое отображение многообразий (размерности n+k в размерность n), то в локальных координатах (картах) это отображение представляет собой отображение шара из R^(n+k) в шар R^(n). Если вы составите матрицу из частных производных этого отображения, то получите матрицу размера n на n+k.
4. Ранг этой матрицы в этих рассуждениях равен n. Видимо, именно ранг матрицы и имеет в виду автор.
5. Если у Вас есть гладкое подмногообразие M^k, то локально всегда можно ввести понятие ортогональности (с помощью касательных пространств).
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 25 окт. 2009 21:41 | IP
|
|
Форум
0.1 Вопросы с неопределенной темой
