Stanislav MM
Начинающий
|
     
Спасибо за разъяснение. Произведение двух нечётных функций даёт – чётную функцию.
Но например функция f(х) = х² + х не является ни чётной, ни нечётной. А как это определить?
235.Решите уравнение f'(х) = 0, если
г) f(х) = х - cos x
f'(х) = (х - cos x )' = 1 + sin x
1 + sin x = 0 sin x = -1 sin x = - π/2
Ответ: - π/2 + 2πn n ϵ Z
Как я понимаю 2πn добавляется, потому, что функция периодическая.
Правильно я решил? В книге такой же ответ.
А вот с другим примером непонятно
234. найдите f'(0) и f'(π) если
г) f(х) = 2 cos x/2
ответ: 0: 1
Казалось бы функция периодическая, но тогда, почему нет 2πn?
Мне непонятно куда подставлять «0» и «π».
В правую или левую часть уравнения?
|
Всего сообщений: 82 | Присоединился: май 2012 | Отправлено: 8 июня 2012 18:33 | IP
|
|
MEHT
Долгожитель
|
Но например функция f(х) = х² + х не является ни чётной, ни нечётной. А как это определить?
Для этого достаточно убедится, что функция не подпадает ни под одно, ни под другое определение; то есть если f(-х) ≠ ±f(х).
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 9 июня 2012 17:20 | IP
|
|
MEHT
Долгожитель
|
235.Решите уравнение f'(х) = 0, если
г) f(х) = х - cos x
f'(х) = (х - cos x )' = 1 + sin x
1 + sin x = 0 sin x = -1 sin x = - π/2
Ответ: - π/2 + 2πn n ϵ Z
Как я понимаю 2πn добавляется, потому, что функция периодическая.
Правильно я решил? В книге такой же ответ.
Правильно.
А вот с другим примером непонятно
234. найдите f'(0) и f'(π) если
г) f(х) = 2 cos x/2
ответ: 0: 1
Казалось бы функция периодическая, но тогда, почему нет 2πn?
Мне непонятно куда подставлять «0» и «π».
В правую или левую часть уравнения?
В первом примере Вы решали уравнение (тригонометрическое). А в этом случае нужно лишь найти значение функции при заданных аргументах. Уравнений решать не требуется.
Сначала ищите производную:
f'(х) = (2 cos x/2)' = -sin(x/2),
потом подставляете вместо икса 0 и пи:
синус нуля - ноль; синус пи пополам - единица.
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 9 июня 2012 17:26 | IP
|
|
Stanislav MM
Начинающий
|
Спасибо за объснения. В двух примерах – разные задания.
222. найти область определения функции.
г) у = √(sinx )
график sin x – это синусоида.
Область значений (по вертикали) равна [ -1; 1 ]
Область определения (по горизонтали) R, то есть все действительные числа числовой прямой.
Это понятно.
Что является графиком функции у = √(sinx )
И как получили данный ответ?
Ответ [ 2πn ; π + 2πn]
|
Всего сообщений: 82 | Присоединился: май 2012 | Отправлено: 12 июня 2012 18:09 | IP
|
|
Stanislav MM
Начинающий
|
Заранее прошу прощения, если вставил вопрос не в ту тему. Но при построении графиков часто используются и тригонометрические функции. По ним у меня меньше вопросов, потому, что тема хорошо раскрыта в книге. Синусоиду можно поднимать, опускать, сдвигать влево ,вправо, сжимать и разжимать, то есть менять период. С иксом как-то менее понятно.
48.
В одной и той же системе координат постройте графики функций.
а) у = 1/х ;у = 1/х + 2 ;у = 1/х-2:
второй график – точно правильный, первый – думаю, что правильный. Насчёт третьего не уверен. Думаю сдвигается влево, на -2 вдоль оси ОХ
|
Всего сообщений: 82 | Присоединился: май 2012 | Отправлено: 13 июня 2012 16:43 | IP
|
|
wanes101
Новичок
|
Здравствуйте
Я занимаюсь подготовкой к экзамену по математике для этого повторяю материал и в том числе решаю задачи по упрощению тригонометрических тождеств . В результате данного процесса на данный момент я не смог упростить следующие тождество:
Помогите пожалуйста, напишите решения, а я подумаю
(Сообщение отредактировал wanes101 14 июня 2012 18:23)
(Сообщение отредактировал wanes101 14 июня 2012 18:23)
|
Всего сообщений: 13 | Присоединился: июнь 2012 | Отправлено: 14 июня 2012 18:00 | IP
|
|
wanes101
Новичок
|
Цитата: Stanislav MM написал 13 июня 2012 16:43
Заранее прошу прощения, если вставил вопрос не в ту тему. Но при построении графиков часто используются и тригонометрические функции. По ним у меня меньше вопросов, потому, что тема хорошо раскрыта в книге. Синусоиду можно поднимать, опускать, сдвигать влево ,вправо, сжимать и разжимать, то есть менять период. С иксом как-то менее понятно.
48.
В одной и той же системе координат постройте графики функций.
а) у = 1/х ;у = 1/х + 2 ;у = 1/х-2:
второй график – точно правильный, первый – думаю, что правильный. Насчёт третьего не уверен. Думаю сдвигается влево, на -2 вдоль оси ОХ
все графики верны
А третий сдвигается вниз ниже нуля при положительных значениях и отрицательных значениях Х.
|
Всего сообщений: 13 | Присоединился: июнь 2012 | Отправлено: 14 июня 2012 18:17 | IP
|
|
ustam
Долгожитель
|
Цитата: wanes101 написал 14 июня 2012 18:00
Здравствуйте
я не смог упростить следующие тождество:
Решается просто: нужно применить формулы суммы синусов и суммы косинусов, после сокращения получится tg(2x)
|
Всего сообщений: 420 | Присоединился: декабрь 2008 | Отправлено: 14 июня 2012 18:55 | IP
|
|
wanes101
Новичок
|
Цитата: ustam написал 14 июня 2012 18:55
Цитата: wanes101 написал 14 июня 2012 18:00
Здравствуйте
я не смог упростить следующие тождество:
Решается просто: нужно применить формулы суммы синусов и суммы косинусов, после сокращения получится tg(2x)
не пойму как это сделать
|
Всего сообщений: 13 | Присоединился: июнь 2012 | Отправлено: 15 июня 2012 5:17 | IP
|
|
MEHT
Долгожитель
|
wanes101,
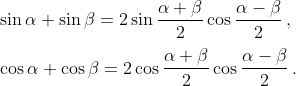
Один угол принимаете равным x, второй 3x.
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 15 июня 2012 12:29 | IP
|
|
|
Форум
1.9 Тригонометрические уравнения
