Elena73
Новичок
|
    
Всем привет! Помогите решить задачу для моего сына 4 класс. Сама решила но сомневаюсь в правильности решения.
Задача: Петя шел на станцию со скоростью 30м/ мин и был уже на расстоянии 560 м от дома, когда отец с собакой отправились вслед за ним . Отец шел со скоростью 50м/мин, а собака бежала со скоростью 100м/ мин. Добежав до Пети, она тут же повернула обратно, добежала до отца, затем обратно до Пети и так безостановочно до тех пор,пока отец не догнал сына. Какой путь проделала собака?
|
Всего сообщений: 2 | Присоединился: апрель 2012 | Отправлено: 4 апр. 2012 13:40 | IP
|
|
MEHT
Долгожитель
|
Отец догонит Петю за время 560/(50 - 30) = 28 [мин.]
(тут мы делим изначальное расстояние между Петей и отцом на скорость их взаимного сближения)
За всё это время собака будет носиться туда-сюда с постоянной по величине скоростью 100 м/мин, а значит в сумме набегает 100*28 = 2800 [м]
(Сообщение отредактировал MEHT 4 апр. 2012 18:14)
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 4 апр. 2012 18:12 | IP
|
|
Elena73
Новичок
|
Спасибо большое выручили
|
Всего сообщений: 2 | Присоединился: апрель 2012 | Отправлено: 4 апр. 2012 18:54 | IP
|
|
lilymurlyka
Начинающий
|
Проверьте, пожалуйста, правильно ли я решила.
Дана функция z=3x^2-xy+x+y и две точки А (1;3); В(1,06; 2,92)
1) Вычислить значение z1 в точке В.
Я решила так.
z1=3*(1,06)^2-1,06*2,92+1,06+2,92=4,3(округленно)
2)Вычислить приближенное значение z1 функции в точке В, исходя из значения z0 функции в точке А и заменив приращение функции при переходе от точке А к точке В дифференциалом
я начала решать так.
Дадим x1 и y1, исходя из значения z0 функции в точке А x1=1, y1=3, приращения дельта x1=0,06; дельта y1=-0,08, вычислим дельта z1 и dx1.
z0(x0;y0)=z0(1;3)=3*1^2-1*3+1+3=4
z1(x1+дельта x1;y1+дельта y1)=z1(1.06;2,92)=3*(1,06)^2-1.06*2.92+1.06+2.92=3.3708-3.0952+1.06+2.92=4.2556
Значит, дельта z=-0,2556
С другой стороны, zx=3-y+y=3; zy=3x^2-x+x=3x^2
Если x=1. y=3, то zx=3, zy=3
Значит dz=0,18-0,24=-0,06
3) оценить в процентах относительную погрешность, получающуюся при замене приращения функции её дифференциалом
я решила так
Абсолютная ошибка равенства дельта z примерно равная dz равно -0,1956, а относительная ошибка -0,1956/-0,2556=0,756(примерно равно)=0,8%
4) составить уравнение касательной плоскости к поверхности z=f(x;y) в точке С (x0;y0;z0)
Я так поняла, что значения для С берем из вышесказанного, значит С (1;3;4)
F(x;y;z)=3x^2-xy+x+y-z=0
|
Всего сообщений: 70 | Присоединился: ноябрь 2011 | Отправлено: 5 апр. 2012 11:11 | IP
|
|
ustam
Долгожитель
|
lilymurlyka Вы все делаете неправильно! Почитайте тему "Применнение дифференциала для приближенных вычислений" в разделе "Функции нескольких переменных"
|
Всего сообщений: 420 | Присоединился: декабрь 2008 | Отправлено: 5 апр. 2012 13:23 | IP
|
|
Oleg210
Новичок
|
Помогите пожалуйста разобраться в решении (уравнение с параметром, решение самого автора учебника):
не очень понятно когда при решении уравнений с модулями и параметрами при рассмотрении различных случаев ставить знаки >=, <=, >, <
или посоветуйте где-нибудь прочитать про это.
|
Всего сообщений: 14 | Присоединился: январь 2011 | Отправлено: 5 апр. 2012 16:59 | IP
|
|
MEHT
Долгожитель
|
В алгебре модуль принято раскрывать так:
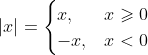
т.е. знак равенства в неравенстве пишут со знаком "больше".
Однако это всего лишь соглашение. Можно везде использовать знаки строгих неравенств и отдельно рассмотреть случаи равенств.
Действительно, автор очень своеобразно раскрывает модуль.
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 5 апр. 2012 19:05 | IP
|
|
lilymurlyka
Начинающий
|
Проверьте, пожалуйста, правильно ли я решила.
Дана функция z=3x^2-xy+x+y и две точки А (1;3); В(1,06; 2,92)
1) Вычислить значение z1 в точке В.
2)Вычислить приближенное значение z1 функции в точке В, исходя из значения z0 функции в точке А и заменив приращение функции при переходе от точке А к точке В дифференциалом
3) оценить в процентах относительную погрешность, получающуюся при замене приращения функции её дифференциалом
4) составить уравнение касательной плоскости к поверхности z=f(x;y) в точке С (x0;y0;z0)
я решила так
По условию x=1, y=3
x+дельта x=1,06
y+дельта y=2,92
Поэтому дельта x=0,06, дельта y=-0,08. Находим точное значение функции в точке В:
z1(В)=3*1,06^2-1,06*2,92+1,06+2,92=3,3708-3,0952+1,06+2,92=4,2556
Пожалуйста, напишите, что дальше делать.
|
Всего сообщений: 70 | Присоединился: ноябрь 2011 | Отправлено: 6 апр. 2012 21:57 | IP
|
|
MEHT
Долгожитель
|
Вам дано
,%5Cqquad%20B(x_0+%5CDelta%20x;%5C,y_0+%5CDelta%20y),%20%5C%5C%5C%5C%20z(x,y)=%203x^2%20-%20xy%20+%20x%20+%20y.)
Приращения аргументов нашли.
Приращение функции найдёте из
=z(x_0,%5C,y_0)+%5CDelta%20z(x_0,%5C,y_0).)
Дифференциал dz - линейная по приращениям аргументов часть приращения функции. В точке A он равен
=%5Cfrac{%5Cpartial%20z}{%5Cpartial%20x}%5C,%5CBig|_{(x_0,%5C,y_0)}%5C,%5CDelta%20x%20%5C%20+%20%5C%20%5Cfrac{%5Cpartial%20z}{%5Cpartial%20y}%5C,%5CBig|_{(x_0,%5C,y_0)}%5C,%5CDelta%20y.)
Заменяя приращение дифференциалом получите приближённое равенство
%5Capprox%20z(x_0,%5C,y_0)+%5C,%5Ctextrm{d}%5C,z(x_0,%5C,y_0).)
Справа стоит приближённое значение z в точке B - то что Вы ищите.
Относительную погрешность найдёте как модуль отношения разности приближённого значения с точным к точному значению z в точке B. И всё это нужно домножить на 100%.
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 7 апр. 2012 1:01 | IP
|
|
MEHT
Долгожитель
|
4) В точке C нормальный вектор к поверхности будет нормальным и к искомой касательной плоскости.
Этим вектором является например
,)
частные производные берутся в точке C.
Искомая плоскость проходит через точку C. Можно строить уравнение касательной плоскости:
+%20%5Cfrac{%5Cpartial%20z}{%5Cpartial%20y}%5Cleft%20(y-y_0%20%5Cright%20)%20-%5Cleft%20(z-z_0%20%5Cright%20)=0.)
(напоминаю снова, что частные производные берутся в точке С)
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 7 апр. 2012 1:19 | IP
|
|
|
Форум
Помогите решить пару задач по математике
