lilymurlyka


Начинающий
|
      
ustam,посмотрите, пожалуйста, правильное ли у меня здесь решение.
найти наименьшее и наибольшее значения функции z=x^2+2y^2+1 в замкнутой области D, заданной системой неравенств x≥0, y≥0, x+y≤3. Сделать чертеж.
Я нашла стационарные точки
dz/dx = 2x
dz/dy = 2y
Точка(0;0) является стационарной и принадлежит области D.
Скажите, пожалуйста, какая фигура будет у этой функции? Треугольник?
|
Всего сообщений: 70 | Присоединился: ноябрь 2011 | Отправлено: 11 апр. 2012 8:58 | IP
|
|
lilymurlyka


Начинающий
|
      
И посмотрите еще, пожалуйста, правильное ли у меня здесь решение.
Даны: функция z=2x^2+3xy+y^2, точка А (2;1) и вектор а(3;4). Найти: 1) grad z в точке А; 2) производную в точке А по направлению вектора а. z=2x^2+3xy+y^2, А(2;1), В(3;4)
1) dz/dx=4x+3y
dz/dy=3x+2y
grad (z)=(dz/dx)+(dz/dy)
grad (z) в точке А(2;1)=(4*2+3*1;3*2+2*1)=(11;8)
2) dz/dа(А)=(grad (z)*а)/sqrt (i)^2+(j)^2
dz/dа(А)=(11;8)*(3;4)/sqrt 3^2+4^2=65/5
|
Всего сообщений: 70 | Присоединился: ноябрь 2011 | Отправлено: 11 апр. 2012 9:20 | IP
|
|
devivan80

Новичок
|
     
Помогите пожалуйста...
С задачей бьюсь уже неделю, всю голову сломал 
Условия задачи.
В пространстве располагаются несколько точек. Точки «А» и «В» лежат на прямой «а». Точка «В» является центром шара. Точки «С» и «D» лежат на прямой «b». Точка «D» принадлежит поверхности шара. Прямые «a» и «b» параллельны.
Известны координаты точек «А» (ax, ay, az), «В» (bx, by, bz), «С» (cx,cy, cz) и радиус сферы равен R.
Необходимо найти координаты точки «D».
внешняя ссылка удалена
Спасибо!
(Сообщение отредактировал devivan80 11 апр. 2012 12:16)
|
Всего сообщений: 2 | Присоединился: апрель 2012 | Отправлено: 11 апр. 2012 12:14 | IP
|
|
oevorona

Новичок
|
      
Помогите найти производную и дифференциал:
y=9x^5 +x^8/корень квадратный x+arccos(2x^3+1)
|
Всего сообщений: 2 | Присоединился: апрель 2012 | Отправлено: 11 апр. 2012 12:46 | IP
|
|
MEHT


Долгожитель
|
     
devivan80, точка D(x,y,z) удовлетворяет уравнению прямой
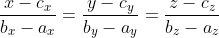
как уравнению, проходящему через точку C с направляющим вектором AB (условие параллельности прямых); также эта точка удовлетворяет уравнению сферы радиуса R с центром в точке B
^2+%5Cleft%20(y-b_y%20%5Cright%20)^2+%5Cleft%20(z-b_z%20%5Cright%20)^2=R^2.)
Нужно совместно решить эти два уравнения. Для этого удобно параметризовать уравнение прямой
,%5C%5C%20y=c_y+k%5Ccdot%20%5Cleft%20(b_y-a_y%20%5Cright%20),%5C%5C%20z=c_z+k%5Ccdot%20%5Cleft%20(b_z-a_z%20%5Cright%20),)
подставить в уравнение сферы и получить квадратное относительно k уравнение. Решая его и найдя k, Вы найдёте и координаты x,y,z из параметрических выражений.
(Сообщение отредактировал MEHT 11 апр. 2012 18:14)
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 11 апр. 2012 18:14 | IP
|
|
devivan80

Новичок
|
     
"MEHT" Огромное спасибо за подробный ответ!
Жаль нет кнопки "Спасибо!"...
|
Всего сообщений: 2 | Присоединился: апрель 2012 | Отправлено: 11 апр. 2012 18:33 | IP
|
|
lilymurlyka


Начинающий
|
      
Скажите, пожалуйста, как строить график у этой задачи?
Вычислить с помощью двойного интегралав полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а>0).(x^2+y^2)^2=a^2(4x^2+y^2)
|
Всего сообщений: 70 | Присоединился: ноябрь 2011 | Отправлено: 12 апр. 2012 2:50 | IP
|
|
lilymurlyka


Начинающий
|
      
И ещё, подскажите. По какой формуле вычислять площадь в декартовых координатах или в полярных?
|
Всего сообщений: 70 | Присоединился: ноябрь 2011 | Отправлено: 12 апр. 2012 5:10 | IP
|
|
lilymurlyka


Начинающий
|
      
Скажите, пожалуйста, как строить график у этой задачи?
Вычислить с помощью двойного интегралав полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а>0).(x^2+y^2)^2=a^2(4x^2+y^2)
И правильное ли решение получилось 5а^2пи/2?
|
Всего сообщений: 70 | Присоединился: ноябрь 2011 | Отправлено: 12 апр. 2012 6:23 | IP
|
|
LORA


Новичок
|
     
Просьба решить следующее задание.
Неравенство:
log 1/7 ( 3 - х )> - 1.
|
Всего сообщений: 1 | Присоединился: апрель 2012 | Отправлено: 12 апр. 2012 9:31 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 Помогите решить пару задач по математике
Помогите решить пару задач по математике

 Форум
Форум

 Математика
Математика

 Помогите решить пару задач по математике
Помогите решить пару задач по математике