lilly


Новичок
|
     
Помогите пожалуйта решить
1)y"'-(1-2)y"-1*2y'=0
y(0)=0, y'(0)=1; y"(0)=2
2)y"-2*2*y'+2^2y=(x+1)e^(1+2)x
y(0)=1;y'(0)=2
Заранее спасибо!
(Сообщение отредактировал lilly 3 нояб. 2009 22:53)
|
Всего сообщений: 30 | Присоединился: май 2009 | Отправлено: 3 нояб. 2009 20:52 | IP
|
|
lilly


Новичок
|
     
я там в условии ошиблась
но уже все исправила
|
Всего сообщений: 30 | Присоединился: май 2009 | Отправлено: 3 нояб. 2009 22:56 | IP
|
|
bukashka


Новичок
|
      
(Сообщение отредактировал bukashka 8 нояб. 2009 18:26)
|
Всего сообщений: 13 | Присоединился: октябрь 2009 | Отправлено: 4 нояб. 2009 0:41 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: lilly написал 3 нояб. 2009 20:52
Помогите пожалуйта решить
1)y"'-(1-2)y"-1*2y'=0
y(0)=0, y'(0)=1; y"(0)=2
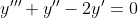
 = z(x) )
 = z'(x) )
 = z''(x) )
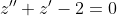
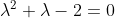

 = Ae^{x} + Be^{-2x} )
 = Ae^{x} + Be^{-2x} )
 = 1 )
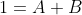
 = Ae^{x} - 2Be^{-2x} )
 = 2 )
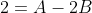
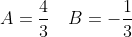
 = \frac{4}{3}e^{x} - \frac{1}{3}e^{-2x} )
 = \frac{4}{3}e^{x} + \frac{1}{6}e^{-2x} + C )
 = 0 )
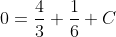
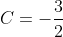
 = \frac{4}{3}e^{x} + \frac{1}{6}e^{-2x} - \frac{3}{2} )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 4 нояб. 2009 12:30 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: lilly написал 3 нояб. 2009 20:52
2)y"-2*2*y'+2^2y=(x+1)e^(1+2)x
y(0)=1;y'(0)=2
e^{3x} )
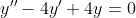
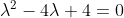
^{2} = 0 )
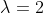 - корень кратности 2 - корень кратности 2
e^{2x} )
e^{3x} )
e^{3x} )
e^{3x} = (3ax + a + 3b)e^{3x} )
e^{3x} = (3a + 9ax + 3a + 9b)e^{3x} = (9ax + 6a + 9b)e^{3x} )
e^{3x} )
e^{3x} - 4(3ax + a + 3b)e^{3x} + 4(ax + b)e^{3x} = (x+1)e^{3x} )
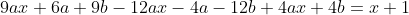
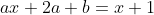
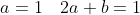
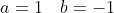
e^{3x} )
 = y_{0} + y_{1} )
 = (Cx + D)e^{2x} + (x - 1)e^{3x} )
 = 1 )
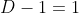
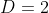
 = (Cx + 2)e^{2x} + (x-1)e^{3x} )
 = Ce^{2x} + 2(Cx + 2)e^{2x} + e^{3x} + 3(x-1)e^{3x} )
 = 2 )
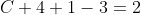
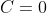
 = 2e^{2x} + (x-1)e^{3x} )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 4 нояб. 2009 13:11 | IP
|
|
Fenja544


Новичок
|
      
Помогите, пожалуйста, решить:
1. Применяя интегральные формулы Коши, вычислить интегралы по замкнутому контуру y(гамма),пробегаемому против часовой стрелки. I=1/(2*п*i) int dz/(z^2*(z-3)) , y(гамма): |z-i|=5
2. Разложить данную функцию в ряд Лорана в окрестности указанной точки z0 и определить область сходимости этого разложения. f(z) = 1/((z^2+1)^2) , z0 = бесконечность
|
Всего сообщений: 40 | Присоединился: октябрь 2009 | Отправлено: 4 нояб. 2009 22:09 | IP
|
|
lilly


Новичок
|
     
RKI
ОГРОРМНОЕ СПАСИБО!
даже не передать словами ,как ВЫ мне помогли!!!!!!!!!!!!!
|
Всего сообщений: 30 | Присоединился: май 2009 | Отправлено: 5 нояб. 2009 2:21 | IP
|
|
bukashka


Новичок
|
      
Помогите, пожалуйста...
1) y''-3y'+2y=e^x/(1+e^(-x)), y(0)=0, y'(0)=0
2) (2y+x*tgy-(y^2)*tgy)dy=dx, y(x=0)=П
|
Всего сообщений: 13 | Присоединился: октябрь 2009 | Отправлено: 8 нояб. 2009 18:27 | IP
|
|
ProstoVasya

Долгожитель
|
     
bukashka
1) Сначала ищите фундаментальную систему решений однородного уравнения. Получите: e^x, e^(2x). Частное решение неоднородного уравнения находите методом вариации произвольных постоянных (метод Лагранжа).
2) Решайте это уравнение относительно неизвестной функции x(y). Здесь линейное уравнение первого порядка.
(Сообщение отредактировал ProstoVasya 8 нояб. 2009 19:49)
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 8 нояб. 2009 19:39 | IP
|
|
bukashka


Новичок
|
      
это ещё больше запутало меня =((((
|
Всего сообщений: 13 | Присоединился: октябрь 2009 | Отправлено: 8 нояб. 2009 22:51 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.3.2 Задачи Коши и краевые задачи для ОДУ
2.3.2 Задачи Коши и краевые задачи для ОДУ

 Форум
Форум

 Математика
Математика

 2.3.2 Задачи Коши и краевые задачи для ОДУ
2.3.2 Задачи Коши и краевые задачи для ОДУ