Форум - 2.3.2 Задачи Коши и краевые задачи для ОДУ [6]

Форум	» Назад на решение задач по физике и термеху
Регистрация \| Профиль \| Войти \| Забытый пароль \| Присутствующие \| Справка \| Поиск

» Добро пожаловать, Гость: Войти | Регистрация

	Форум Математика 2.3.2 Задачи Коши и краевые задачи для ОДУ
	Отметить все сообщения как прочитанные [ Помощь ] » Добро пожаловать на форум "Математика" «

Переход к теме
<< Назад Вперед >>

Несколько страниц [ 1 2 3 4 5 6 7 8 9 10 11 12 13 ]
Модераторы: Roman Osipov, RKI, attention, paradise

natafka

Новичок
И вот еще одна )))) помогите , пожалуйста, еще разок )))))
Найти общее решение дифференциального уравнения

y''-2y'+у=-12cos2x-9sin2x

Всего сообщений: 49 | Присоединился: ноябрь 2008 | Отправлено: 23 сен. 2009 13:03 | IP

RKI

Долгожитель

Цитата: natafka написал 23 сен. 2009 13:03
И вот еще одна )))) помогите , пожалуйста, еще разок )))))
Найти общее решение дифференциального уравнения

y''-2y'+у=-12cos2x-9sin2x

y'' - 2y' + y = - 12cos2x - 9sin2x

y'' - 2y' + y = 0

(a^2) - 2a + 1 = 0
(a - 1)^2 = 0
a - 1 = 0
a = 1 - корень кратности 2

y(одн) = (C + Dx)(e^x)

y'' - 2y' + y = - 12cos2x - 9sin2x

y(частн) = Asin2x + Bcos2x

y'(частн) = 2Acos2x - 2Bsin2x

y''(частн) = - 4Asin2x - 4Bcos2x

y''(частн) - 2y'(частн) + y(частн) = - 12cos2x - 9sin2x

- 4Asin2x - 4Bcos2x - 4Acos2x + 4Bsin2x + Asin2x + Bcos2x = - 12cos2x - 9sin2x

(- 4A + 4B + A)sin2x + (- 4B - 4A + B)cos2x = - 12cos2x - 9sin2x

(4B - 3A)sin2x + (- 3B - 4A)cos2x = - 12cos2x - 9sin2x

при sin2x: 4B - 3A = - 9
при cos2x: - 3B - 4A = - 12

A = 3; B = 0

y(частн) = Asin2x + Bcos2x

y(частн) = 3sin2x

y(x) = y(одн) + y(частн)

y(x) = (C + Dx)(e^x) + 3sin2x

Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 23 сен. 2009 13:32 | IP

natafka

Новичок
Спасибочки оооогромное вам!!!!Очень благодарна за помощь ))))

Всего сообщений: 49 | Присоединился: ноябрь 2008 | Отправлено: 23 сен. 2009 14:52 | IP

bukashka

Новичок
...

(Сообщение отредактировал bukashka 4 нояб. 2009 0:37)

Всего сообщений: 13 | Присоединился: октябрь 2009 | Отправлено: 31 окт. 2009 22:07 | IP

vovancheg

Новичок
помогите решить
наити частное решение д.у. увледотваряющее начальным условиям
xy'-y=x(в квадрате)*(cosx) нач условие y(п/2)=п/2

Всего сообщений: 6 | Присоединился: ноябрь 2009 | Отправлено: 2 нояб. 2009 15:35 | IP

vovancheg

Новичок
ну ппожалуйста помогите решить завтра над сдавать контрошку(

Всего сообщений: 6 | Присоединился: ноябрь 2009 | Отправлено: 2 нояб. 2009 16:01 | IP

Fenja544

Новичок
Помогите, пожалуйста, решить:
1. Применяя интегральные формулы Коши, вычислить интегралы по замкнутому контуру y(гамма),пробегаемому против часовой стрелки. I=1/(2*п*i) int dz/(z^2*(z-3)) , y(гамма): |z-i|=5

2. Разложить данную функцию в ряд Лорана в окрестности указанной точки z0 и определить область сходимости этого разложения. f(z) = 1/((z^2+1)^2) , z0 = бесконечность

Всего сообщений: 40 | Присоединился: октябрь 2009 | Отправлено: 2 нояб. 2009 18:55 | IP

Kisenochek

Новичок
помогите пожалуйста
y''+5y'+6y=f(x)
a)f(x)=18x^2
b)f(x)=(4x+3)e^(-2x)
буду очень благодарна

Всего сообщений: 16 | Присоединился: ноябрь 2009 | Отправлено: 3 нояб. 2009 17:09 | IP

RKI

Долгожитель

Цитата: Kisenochek написал 3 нояб. 2009 17:09
помогите пожалуйста
y''+5y'+6y=f(x)
a)f(x)=18x^2
b)f(x)=(4x+3)e^(-2x)

$y'' + 5y' + 6y = 0$

$\lambda^{2} + 5\lambda + 6 = 0$

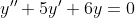
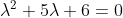
$(\lambda + 2)(\lambda + 3) = 0$

$\lambda = -2 \ \ \ \lambda = -3$

$y_{0} = Ce^{-2x} + De^{-3x}$

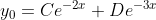
а)
$y'' + 5y' + 6y = 18x^{2}$

$y_{1} = ax^{2} + bx + c$
$y'_{1} = 2ax + b$
$y''_{1} = 2a$

$y''_{1} + 5y'_{1} + 6y_{1} = 18x^{2}$

$2a + 10ax + 5b + 6ax^{2} + 6bx + 6c = 18x^{2}$

$6a = 18 \ \ \ 10a + 6b = 0 \ \ \ 2a + 5b + 6c = 0$

$a = 3 \ \ \ b = -5 \ \ \ c = \frac{19}{6}$

$y_{1} = 3x^{2} - 5x + \frac{19}{6}$

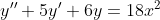
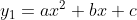
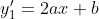
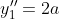
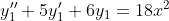
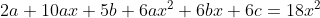
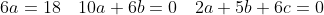
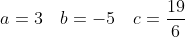
$y(x) = y_{0} + y_{1}$

$y(x) = Ce^{-2x} + De^{-3x} + 3x^{2} - 5x + \frac{19}{6}$

Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 3 нояб. 2009 19:41 | IP

RKI

Долгожитель

Цитата: Kisenochek написал 3 нояб. 2009 17:09
помогите пожалуйста
y''+5y'+6y=f(x)
a)f(x)=18x^2
b)f(x)=(4x+3)e^(-2x)
буду очень благодарна

б)
$y'' + 5y' + 6y = (4x+3)e^{-2x}$

$y_{1} = x(ax+b)e^{-2x} = (ax^{2} + bx)e^{-2x}$

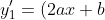$y'_{1} = (2ax + b)e^{-2x} - 2(ax^{2} + bx)e^{-2x} = (-2ax^{2} + 2ax - 2bx + b)e^{-2x}$

$y''_{1} = (-4ax + 2a - 2b)e^{-2x} - 2(-2ax^{2} + 2ax - 2bx + b)e^{-2x} = (4ax^{2} - 8ax + 4bx + 2a - 4b)e^{-2x}$

$y''_{1} + 5y'_{1} + 6y_{1} = (4x+3)e^{-2x}$

$(4ax^{2} - 8ax + 4bx + 2a - 4b)e^{-2x} + (-10ax^{2} + 10ax - 10bx + 5b)e^{-2x} + (6ax^{2} + 6bx)e^{-2x} = (4x+3)e^{-2x}$

$4ax^{2} - 8ax + 4bx + 2a - 4b - 10ax^{2} + 10ax - 10bx + 5b + 6ax^{2} + 6bx = 4x + 3$

$2ax + 2a + b = 4x + 3$

$2a = 4 \ \ \ 2a + b = 3$

$a = 2 \ \ \ b = - 1$

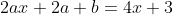
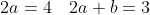
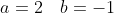
$y_{1} = (2x^{2} - x)e^{-2x}$

$y(x) = y_{0} + y_{1}$

$y(x) = Ce^{-2x} + De^{-3x} + (2x^{2} - x)e^{-2x}$

Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 3 нояб. 2009 20:18 | IP

Отправка ответа:

Имя пользователя Вы зарегистрировались?
Пароль Забыли пароль?
Сообщение
Использование HTML запрещено
Использование IkonCode разрешено
Смайлики разрешены

Опции отправки
Добавить подпись?
Получать ответы по e-mail?
Разрешить смайлики в этом сообщении?
Просмотреть сообщение перед отправкой? Да Нет

Переход к теме
<< Назад Вперед >> Несколько страниц [ 1 2 3 4 5 6 7 8 9 10 11 12 13 ]