oc


Новичок
|
      
найти фундаментальную систему решений и выписать общее решение

Заранее спасибо
помогите плиз!
(Сообщение отредактировал attention 7 дек. 2009 6:43)
|
Всего сообщений: 8 | Присоединился: октябрь 2009 | Отправлено: 26 окт. 2009 16:18 | IP
|
|
mysunny

Новичок
|
     
Не подскажите как решить:
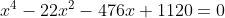
(Сообщение отредактировал attention 7 дек. 2009 6:44)
|
Всего сообщений: 1 | Присоединился: декабрь 2009 | Отправлено: 7 дек. 2009 0:49 | IP
|
|
Kutko Kseniya


Новичок
|
      
(6-x)})
Только напишите пожалуйсто решение уравнения, а не только ответ.
(Сообщение отредактировал attention 8 дек. 2009 14:37)
|
Всего сообщений: 5 | Присоединился: ноябрь 2009 | Отправлено: 8 дек. 2009 12:35 | IP
|
|
attention 


Долгожитель
|
      
Цитата: Kutko Kseniya написал 8 дек. 2009 11:35
(6-x)})
Только напишите пожалуйсто решение уравнения, а не только ответ.
Kutko Kseniya, упростите и получите квадратное уравнение и решайте с учетом ОДЗ.
ОДЗ: 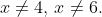
(6 - x)} \, \Leftrightarrow \, \frac{5}{2} = \frac{x}{(4 - x)(6 - x)} \,\Leftrightarrow \hfill \\ \Leftrightarrow \, 5(4 - x)(6 - x) = 2x \, \Leftrightarrow \, 120 - 50x + 5x^2 = 2x \, \Leftrightarrow \hfill \\ \Leftrightarrow \, 5x^2 - 52x + 120 = 0 \, \Leftrightarrow \, x_{1,2} = \frac{26 \pm \sqrt {26^2 - 5 \cdot 120} }{5} = \frac{26 \pm 2\sqrt{19} }{5}. \hfill \\ \end{gathered})
Т.е. оба корня являются решениями изначального уравнения, т.к. входят в ОДЗ.
(Сообщение отредактировал attention 8 дек. 2009 15:03)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 8 дек. 2009 15:55 | IP
|
|
elmira nasretdin


Новичок
|
     
Здравствуйте! Помогите, пожалуйста решить.Для какого q уравнение x^3-2*x-q=0 имеет только один действительный корень?
|
Всего сообщений: 12 | Присоединился: декабрь 2009 | Отправлено: 8 дек. 2009 17:56 | IP
|
|
paradise 

Долгожитель
|
       
Здесь очень простое условие, у Вас будет один действительный корень (и два комплексных), когда дискриминант > 0. Запишем его:

|
Всего сообщений: 428 | Присоединился: ноябрь 2008 | Отправлено: 8 дек. 2009 21:27 | IP
|
|
elmira nasretdin


Новичок
|
     
Спасибо огромное за помощь. У меня был не такой ответ,у вас он точный. Помогите разобраться еще с одним заданием.Пожалуйста.Нужно построить график функции p=(1+sinф)/cosф в полярной системе координат.Здесь как? Подставлять сразу значения углов и находить p или нужны какие-то преобразования?График я построю сама.
|
Всего сообщений: 12 | Присоединился: декабрь 2009 | Отправлено: 9 дек. 2009 13:30 | IP
|
|
elmira nasretdin


Новичок
|
     
Здравствуйте! Почему вы молчите? Помогите, пожалуйста, разобраться с вышеуказанным заданием. Очень вас прошу.Заранее благодарна.
|
Всего сообщений: 12 | Присоединился: декабрь 2009 | Отправлено: 11 дек. 2009 10:34 | IP
|
|
ProstoVasya

Долгожитель
|
     
mysunny
Один корень равен 8. Многочлен можно разложить на множители
(x-8)(x^3 + 8x^2 +42x-140)
У многочлена x^3 + 8x^2 +42x-140 один вещественный корень, который можно найти по методу Кардано.
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 12 дек. 2009 17:17 | IP
|
|
ProstoVasya

Долгожитель
|
     
elmira nasretdin
При построении графика удобно перейти к параметрическому заданию кривой (ф - параметр). Тогда при -п/2 < ф <п/2 (область определения)
х = p cosф = 1+sinф
y = p sinф = (1+sinф) tgф
Нужно только внимательно проследить за поведением при ф -> -п/2
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 12 дек. 2009 17:24 | IP
|
|

 Форум
Форум

 Математика
Математика

 1.7 Алгебраические уравнения
1.7 Алгебраические уравнения

 Форум
Форум

 Математика
Математика

 1.7 Алгебраические уравнения
1.7 Алгебраические уравнения