Roman Osipov 
Долгожитель
|
        
Алгебраические уравнения.
|
Всего сообщений: 2356 | Присоединился: май 2007 | Отправлено: 18 апр. 2009 13:34 | IP
|
|
engineersfinger
Новичок
|
Подскажите пожалуйста способ решения в рамках школьной математики
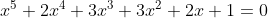
(Сообщение отредактировал attention 7 дек. 2009 2:07)
|
Всего сообщений: 4 | Присоединился: май 2009 | Отправлено: 29 мая 2009 14:29 | IP
|
|
Olegmath2
Полноправный участник
|
Цитата: engineersfinger написал 29 мая 2009 14:29
Подскажите пожалуйста способ решения в рамках школьной математики
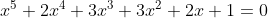
Задача. Решить уравнение x^5+2x^4+3x^3+3x^2+2x+1=0, (*).
Решение. Введём обозначение P(x)= x^5+2x^4+3x^3+3x^2+2x+1.
Заметим, что (*) – это алгебраическое уравнение с целыми коэффициентами.
Пусть x0 – целый корень уравнения (*), тогда он должен быть делителем свободного члена, равного 1. Отсюда следует, что x0= 1 или x0=-1.
Проверка показывает, что P(1)=12 => x=1 не является корнем уравнения (*); P(-1)=0 => x=-1 – корень уравнения (*) => [по следствию из теоремы Безу]=> P(x) нацело делится на (x-x0), т.е. на (x+1). Частное от деления P(x) на (x+1) можно найти методом деления углом или с помощью схемы Горнера (хотя можно применить и метод неопределённых коэффициентов). В результате деления получим:
(x^5+2x^4+3x^3+3x^2+2x+1) x+1)= x^4+x^3+2x^2+x+1.
Отсюда следует, (*)<=> (x+1)( x^4+x^3+2x^2+x+1)=0.
I. x+1=0; x=-1,
II. x^4+x^3+2x^2+x+1=0;
(x^4+2x^2+1)+(x^3+x)=0;
(x^2+1)^2+x(x^2+1)=0;
(x^2+1)(x^2+1+x)=0;
1) x^2+1=0
x^2=-1;
корней нет
2) x^2+x+1=0;
D=1-4=-3
корней нет.
Ответ: -1.
Данное уравнение решено в области действительных чисел!
Цитата: engineersfinger написал 29 мая 2009 14:29
Подскажите пожалуйста способ решения в рамках школьной математики.
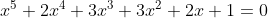
А вот школьный метод решения – это метод группировки и разложения на множители. Этот метод мне не совсем нравится, потому что приходится угадывать не совсем очевидную группировку слагаемых!
+(2x^4+2x^2)+(2x^3+2x)+(x^2+1)=0; \hfill \\ x^3(x^2+1)+2x^2(x^2+1)+2x(x^2+1)+(x^2+1)=0; \hfill \\ (x^2+1)(x^3+2x^2+2x+1)=0; \hfill \\ (x^2+1)((x^3+1)+2x(x+1))=0 \hfill \\ \end{gathered})
Дальше, думаю, доделаете сами!
(Сообщение отредактировал attention 7 дек. 2009 6:26)
|
Всего сообщений: 235 | Присоединился: февраль 2009 | Отправлено: 29 мая 2009 14:58 | IP
|
|
engineersfinger
Новичок
|
Olegmath2, спасибо вам большое !
|
Всего сообщений: 4 | Присоединился: май 2009 | Отправлено: 29 мая 2009 19:04 | IP
|
|
Snigur
Новичок
|
Кто может мне помочь?
(Сообщение отредактировал attention 7 дек. 2009 2:19)
|
Всего сообщений: 19 | Присоединился: июль 2009 | Отправлено: 18 июля 2009 12:02 | IP
|
|
RKI
Долгожитель
|
Цитата: Snigur написал 18 июля 2009 12:02
Кто может мне помочь?
sqrt(3-x) - x - 3 = 0
sqrt(3-x) = x + 3
Воведем левую и правую часть уравнения в квадрат
3 - x = (x+3)^2
3 - x = x^2 + 6x + 9
x^2 + 7x + 6 = 0
(x+6)(x+1) = 0
x+6 = 0; x+1 = 0
x = -6; x = -1
Проверим полученное решение:
x = -6
sqrt(3-x) - x - 3 = sqrt(3+6) + 6 - 3 = sqrt(9) + 3 = 3 +3 = 6 =/= 0 => x=-6 не является решением исходного уравнения
x=-1
sqrt(3-x) - x - 3 = sqrt(3+1) + 1 - 3 = sqrt(4) - 2 = 2 - 2 = 0
=> x=-1 является решением исходного уравнения
ответ. -1
(Сообщение отредактировал attention 8 дек. 2009 15:09)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 18 июля 2009 12:09 | IP
|
|
Snigur
Новичок
|
Спасибо огромное
|
Всего сообщений: 19 | Присоединился: июль 2009 | Отправлено: 18 июля 2009 12:23 | IP
|
|
555554
Новичок
|
X в степени 4 - 7X в кубе + 14Х в квадрате - 7Х +1=0
2Х в степени 4 + Х в кубе - 11 Х в квадрате + Х + 2 =0
ПОМОГИТЕ РЕШИТЬ С ПОМОЩЬЮ ТЕОРЕМЫ БЕЗУ.
|
Всего сообщений: 8 | Присоединился: сентябрь 2009 | Отправлено: 23 сен. 2009 17:48 | IP
|
|
Roman Osipov
Долгожитель
|
1.
корни
x=2+sqrt(3), x=2-sqrt(3), x=(1/2)(3+sqrt(5)), x=(1/2)(3-sqrt(5)).
2.
корни
x=1/2, x=2, x=(1/2)(-3+sqrt(5)), x=(1/2)(-3-sqrt(5)).
|
Всего сообщений: 2356 | Присоединился: май 2007 | Отправлено: 24 сен. 2009 16:36 | IP
|
|
Chuchi
Новичок
|
Помогите, пожалуйста, решить уравнения:
1. /x-1/ = 2x-3
2. 5tgx + 1 = 3/cos^2x
3. sqrt(5x^2 + 4x) + sqrt(5x^2 - x) = 5
И систему уравнений:
4^(y - 3x) = 1/64
4^(y - x - 5) = 16
|
Всего сообщений: 36 | Присоединился: апрель 2009 | Отправлено: 25 сен. 2009 17:01 | IP
|
|
Форум
1.7 Алгебраические уравнения
