RKI 


Долгожитель
|
     
Цитата: polinka написал 9 марта 2010 12:15
1xy'sin(y/x)+x=ysin(y/x)


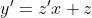
sinz + x = zxsinz )
sinz + 1 = zsinz )
 + zsinz + 1 = zsinz )
 + 1 = 0 )
 = - 1 )
\frac{dz}{dx} = - 1 )
dz = - \frac{dx}{x} )
dz = - \int\frac{dx}{x} )
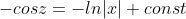
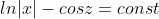

|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 9 марта 2010 13:34 | IP
|
|
polinka

Новичок
|
      
большое спасибо Вам за примерчик!
(Сообщение отредактировал polinka 9 марта 2010 13:48)
|
Всего сообщений: 7 | Присоединился: март 2010 | Отправлено: 9 марта 2010 13:44 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: polinka написал 9 марта 2010 12:15
2xy+y^2=(2x^2+xy)y'
y' )

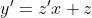
(z'x + z) )
(z'x + z) )
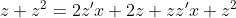

 = - z )
\frac{dz}{dx} = -z )
dz = - \frac{dx}{x} )
dz = - \int \frac{dx}{x} )
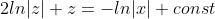


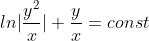
(Сообщение отредактировал RKI 9 марта 2010 13:50)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 9 марта 2010 13:48 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: polinka написал 9 марта 2010 12:15
3xy'ln(y/x)=x+yln(y/x)
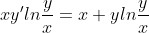

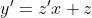
lnz = x + xzlnz )
lnz = 1 + zlnz )


\frac{dz}{dx} = 1 )
dz = \frac{dx}{x} )
dz = \int\frac{dx}{x} )
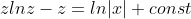
 = ln|x| + const )
 = ln|x| + const )
 - ln|x| = const )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 9 марта 2010 13:57 | IP
|
|
polinka

Новичок
|
      
Огромное спасибо!!!! Вы просто гений)))) и у вас замечательный форум)))
|
Всего сообщений: 7 | Присоединился: март 2010 | Отправлено: 9 марта 2010 13:57 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: polinka написал 9 марта 2010 12:15
4xyy'=y^2+2x^2
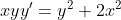

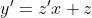
 = z^{2}x^{2} + 2x^{2} )
 = z^{2} + 2 )
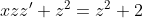
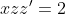


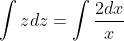
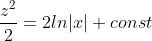


|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 9 марта 2010 14:04 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: polinka написал 9 марта 2010 12:15
5y'=(y/x)+cos(y/x)


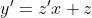


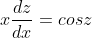


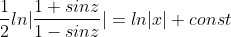

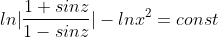
}| = const )
} = const )
} = const )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 9 марта 2010 14:13 | IP
|
|
polinka

Новичок
|
      
Спасибочки))))
(Сообщение отредактировал polinka 11 марта 2010 11:08)
|
Всего сообщений: 7 | Присоединился: март 2010 | Отправлено: 9 марта 2010 14:26 | IP
|
|
Anna90


Новичок
|
     
Пожалуйста, помогите доказать существование предельного цикла при E<A(1-A)/(1+A) (E,A,M>0 - параметры):
dx/dt = x - xy/(1+Ax) - Ex^2
dy/dt = -My + Mxy/(1+Ax)
Особая точка:
x = 1/(1-A)
y = 1/(1-A) - E/((1-A)^2)
x,y>0, т.е. 0<A+E<1
Матрица Якоби:
J [1][1] = A + E - 2E/(1-A)
J [1][2] = -1
J [2][1] = M(1-A-E)
J [2][2] = 0
Характеристический многочлен:
lambda^2 - lambda(A + E - 2E/(1-A)) + M(1-A-E) = 0
(A + E - 2E/(1-A)) обращается в ноль при E=A(1-A)/(1+A). Дальше не соображу.
(Сообщение отредактировал Anna90 16 мая 2010 11:25)
|
Всего сообщений: 11 | Присоединился: сентябрь 2009 | Отправлено: 16 мая 2010 11:25 | IP
|
|
iren a


Новичок
|
     
Помогите, пожалуйста! Срочно нужно решить систему уравнений!!!
{ 2x - y + 3x = 9
3x - 5y + z = 4
4x - 7y + 2z = 5
|
Всего сообщений: 1 | Присоединился: март 2011 | Отправлено: 31 марта 2011 10:05 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.3.3 Системы обыкновенных дифференциальных уравнений
2.3.3 Системы обыкновенных дифференциальных уравнений

 Форум
Форум

 Математика
Математика

 2.3.3 Системы обыкновенных дифференциальных уравнений
2.3.3 Системы обыкновенных дифференциальных уравнений