Trushkov

Долгожитель
|
        
Выражаете x из второго уравнения (x=y'-y), подставляете в первое (y''-y'=y'-y-4y). Получается уравнение второго порядка с постоянными коэффициентами.
|
Всего сообщений: 273 | Присоединился: январь 2006 | Отправлено: 20 окт. 2009 10:32 | IP
|
|
lolechka


Начинающий
|
     
Здравствуйте, подскажите как дальше дорешать систему дифференциальных уравнений с помощью характеристического уравнения
x'=-2x
y'=y
решаю так
составляем характеристическое уравнение и решаем его:
|-2-L 0 |
|0 1-L)|=0 ;
(-2-L)(1-L)=0;
L_1=1; L_2=-2
Решение системы ищем в виде:
x_1=A_1 e^(L_1 x)=A_1 e^x; y_1=B_1 e^(L_1 x)=B_1 e^x
x_2=A_2 e^(L_2 x)=A_2 e^(-2x); y_2=B_2 e^(L_2 x)=B_2 e^(-2x).
а дальше что то туплю
(Сообщение отредактировал lolechka 9 дек. 2009 7:09)
|
Всего сообщений: 54 | Присоединился: октябрь 2008 | Отправлено: 9 дек. 2009 7:03 | IP
|
|
attention 


Долгожитель
|
      
Цитата: lolechka написал 9 дек. 2009 6:03
Здравствуйте, подскажите как дальше дорешать систему дифференциальных уравнений с помощью характеристического уравнения
x'=-2x
y'=y
решаю так
составляем характеристическое уравнение и решаем его:
|-2-L 0 |
|0 1-L)|=0 ;
(-2-L)(1-L)=0;
L_1=1; L_2=-2
Решение системы ищем в виде:
x_1=A_1 e^(L_1 x)=A_1 e^x; y_1=B_1 e^(L_1 x)=B_1 e^x
x_2=A_2 e^(L_2 x)=A_2 e^(-2x); y_2=B_2 e^(L_2 x)=B_2 e^(-2x).
а дальше что то туплю
lolechka, во-первых, у вас  и и  не друг от друга, а они зависят от не друг от друга, а они зависят от  ; во-вторых, оба уравнения системы не связаны между собой; т.е. просто каждое уравнение системы решаете отдельно относительно переменной ; во-вторых, оба уравнения системы не связаны между собой; т.е. просто каждое уравнение системы решаете отдельно относительно переменной  : :
=Ce^{- 2t}, \hfill \\\!y\left( t \right)=Ce^t. \hfill \\ \end{gathered}\right.)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 9 дек. 2009 8:09 | IP
|
|
Stalker


Новичок
|
       
Помогите решить систему уравнений записав в матричной форме

(Сообщение отредактировал Stalker 3 марта 2010 16:28)
|
Всего сообщений: 5 | Присоединился: март 2010 | Отправлено: 3 марта 2010 15:51 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Stalker написал 3 марта 2010 15:51
Помогите решить систему уравнений записав в матричной форме

(Сообщение отредактировал Stalker 3 марта 2010 16:28)
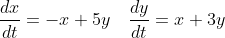
X = x
y
X' = x'
y'
A = -1 5
1 3
X' = AX
Найдем собственные значения a матрицы A.
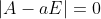
|-1-a 5 | = 0
| 1 3-a|
(3-a) = 0 )
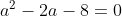
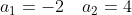
Решение системы дифференциальных уравнений имеет вид:
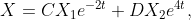
где 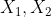 - собственные векторы матрицы A, соответтсвующие собственным значениям -2 и 4 соответственно. - собственные векторы матрицы A, соответтсвующие собственным значениям -2 и 4 соответственно.
Найдем 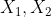
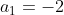
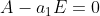
1 5 0
1 5 0
1 5 0
0 0 0
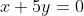
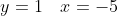
X1 = -5
1
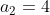
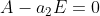
-5 5 0
1 -1 0
0 0 0
1 -1 0
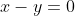
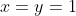
X2 = 1
1
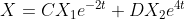
 = -5Ce^{-2t} + De^{4t} \ \ \ y(t) = Ce^{-2t} + De^{4t} )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 5 марта 2010 14:46 | IP
|
|
Tapik

Новичок
|
       
В точках x1=0 и x2=6 для функции f(x) установить непрерывность или определитель характер точек разрыва. Нарисовать график функции f(x) в окресностях этих точек:
Вот такая вот задачка. Помогите решить, очень надо
пожалуйстааа
a) f(x)=5/(-2+2^6/x)
l5/6*(x+6), если -00<x<0
b) f(x)=l5/36*(x-36), если 0<=x<=6
l 5, если 6<x<+00
|
Всего сообщений: 12 | Присоединился: март 2010 | Отправлено: 5 марта 2010 20:48 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Tapik написал 5 марта 2010 20:48
В точках x1=0 и x2=6 для функции f(x) установить непрерывность или определитель характер точек разрыва. Нарисовать график функции f(x) в окресностях этих точек:
Вот такая вот задачка. Помогите решить, очень надо
пожалуйстааа
a) f(x)=5/(-2+2^6/x)
l5/6*(x+6), если -00<x<0
b) f(x)=l5/36*(x-36), если 0<=x<=6
l 5, если 6<x<+00
f(x) = {(5/6)(x+6), x < 0
{(5/36)(x-36), 0 <= x <= 6
{5, x > 6
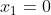
 = \lim\limits_{x \to -0} \frac{5}{6}(x+6) = \frac{5}{6}(0+6) = 5 )
 = \lim\limits_{x \to +0} \frac{5}{36}(x-36) = \frac{5}{36}(0-36) = - 5 )
 \ne \lim\limits_{x \to + 0} f(x) )
Следовательно, точка 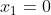 - точка разрыва первого рода. - точка разрыва первого рода.
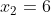
 = \lim\limits_{x \to 6-0} \frac{5}{36}(x-36) = \frac{5}{36}(6-36) = - \frac{25}{6} )
 = \lim\limits_{x \to 6+0} 5 = 5 )
 \ne \lim\limits_{x \to 6+0} f(x) )
Следовательно, точка 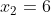 - точка разрыва первого рода. - точка разрыва первого рода.
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 6 марта 2010 10:44 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Tapik написал 5 марта 2010 20:48
В точках x1=0 и x2=6 для функции f(x) установить непрерывность или определитель характер точек разрыва. Нарисовать график функции f(x) в окресностях этих точек:
Вот такая вот задачка. Помогите решить, очень надо
пожалуйстааа
a) f(x)=5/(-2+2^6/x)
l5/6*(x+6), если -00<x<0
b) f(x)=l5/36*(x-36), если 0<=x<=6
l 5, если 6<x<+00
 = \frac{5}{2^{\frac{6}{x} } - 2} )
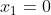
 = \lim\limits_{x \to -0} \frac{5}{2^{\frac{6}{x} } - 2} = \frac{5}{0 - 2} = - 2.5 )
 = \lim\limits_{x \to +0} \frac{5}{2^{\frac{6}{x} } - 2} = 0 )
 \ne \lim\limits_{x \to + 0} f(x) )
Следовательно, точка 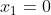 - точка разрыва первого рода. - точка разрыва первого рода.
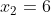
 = \lim\limits_{x \to 6} \frac{5}{2^{\frac{6}{x} } - 2} = \lim\limits_{x \to 6} \frac{5}{2(2^{\frac{6}{x} - 1} - 1)} = )
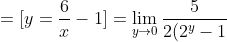} = \lim\limits_{y \to 0} \frac{5y(ln2)}{2y(ln2)(2^{y} - 1)} = )
}{2^{y} - 1} ]*[\lim\limits_{y \to 0} \frac{5}{2y(ln2)} ] = \lim\limits_{y \to 0} \frac{5}{2y(ln2) } = \infty )
Следовательно, точка 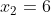 - точка разрыва второго рода. - точка разрыва второго рода.
(Сообщение отредактировал RKI 6 марта 2010 11:06)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 6 марта 2010 10:59 | IP
|
|
Stalker


Новичок
|
       
Цитата: RKI написал 5 марта 2010 14:46
Спасибо.!
|
Всего сообщений: 5 | Присоединился: март 2010 | Отправлено: 9 марта 2010 9:24 | IP
|
|
polinka

Новичок
|
      
1xy'sin(y/x)+x=ysin(y/x)
2xy+y^2=(2x^2+xy)y'
3xy'ln(y/x)=x+yln(y/x)
4xyy'=y^2+2x^2
5y'=(y/x)+cos(y/x)
|
Всего сообщений: 7 | Присоединился: март 2010 | Отправлено: 9 марта 2010 12:15 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.3.3 Системы обыкновенных дифференциальных уравнений
2.3.3 Системы обыкновенных дифференциальных уравнений

 Форум
Форум

 Математика
Математика

 2.3.3 Системы обыкновенных дифференциальных уравнений
2.3.3 Системы обыкновенных дифференциальных уравнений