Jane Smit

Новичок
|
     
(Сообщение отредактировал Jane Smit 20 окт. 2009 22:32)
|
Всего сообщений: 2 | Присоединился: октябрь 2009 | Отправлено: 20 окт. 2009 22:22 | IP
|
|
pavzer


Новичок
|
     
Посмотрите пожайлусьа правильно или нет ???
lim (tg 3x)/(sin 2x)=0/0
x->0
=lim (tgx*(3-tg^2x))/((1-3tg^2x)*2*sinx*cosx)=
x->0
=lim (sinx*(3-tg^2x))/(2*cos^2x*sinx(1-3tg^2x))=
x->0
=lim (3-tg^2x)/(2(1-3tg^2x)cos^2x)=
x->0
=3/2=1.5
|
Всего сообщений: 4 | Присоединился: октябрь 2009 | Отправлено: 24 окт. 2009 11:10 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: pavzer написал 24 окт. 2009 11:10
Посмотрите пожайлусьа правильно или нет ???
lim (tg 3x)/(sin 2x)=0/0
x->0
=lim (tgx*(3-tg^2x))/((1-3tg^2x)*2*sinx*cosx)=
x->0
=lim (sinx*(3-tg^2x))/(2*cos^2x*sinx(1-3tg^2x))=
x->0
=lim (3-tg^2x)/(2(1-3tg^2x)cos^2x)=
x->0
=3/2=1.5
*(3x)*(2x)}{(sin2x)*(3x)*(2x)} = )

y = 3x
z = 2x
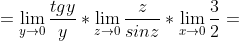
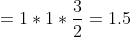
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 24 окт. 2009 12:40 | IP
|
|
tatka111


Новичок
|
     
Помогите пожалуйста вычислить интеграл:
lim(х->- 2) (√(10+х-x^2 )+х)/(√(2-7х)+2х)
(Сообщение отредактировал tatka111 25 окт. 2009 13:34)
|
Всего сообщений: 22 | Присоединился: октябрь 2009 | Отправлено: 25 окт. 2009 13:33 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: tatka111 написал 25 окт. 2009 13:33
Помогите пожалуйста вычислить интеграл:
lim(х->- 2) (√(10+х-x^2 )+х)/(√(2-7х)+2х)
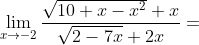
(\sqrt{10+x-x^{2} } - x)}{(\sqrt{2-7x} + 2x)(\sqrt{10+x-x^{2} } - x)} = )
(\sqrt{10+x-x^{2} } - x)} = )
(\sqrt{10+x-x^{2} } - x)} = )
(\sqrt{2-7x} - 2x)}{(\sqrt{2-7x} + 2x)(\sqrt{10+x-x^{2} } - x)(\sqrt{2-7x} - 2x)} = )
(\sqrt{2-7x} - 2x)}{(2 - 7x - 4x^{2})(\sqrt{10+x-x^{2} } - x)} = )
(\sqrt{2-7x} - 2x)}{(2 - 7x - 4x^{2})(\sqrt{10+x-x^{2} } - x)} = )
(5-2x)(\sqrt{2-7x} - 2x)}{(x+2)(1-4x)(\sqrt{10+x-x^{2} } - x)} = )
(\sqrt{2-7x} - 2x)}{(1-4x)(\sqrt{10+x-x^{2} } - x)} = )
(\sqrt{2+14} + 4)}{(1+8)(\sqrt{10-2-4} + 2)} = \frac{9*8}{9*4} = 2 )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 25 окт. 2009 16:18 | IP
|
|
tatka111


Новичок
|
     
RKI Огромное СПАСИБО!!!
|
Всего сообщений: 22 | Присоединился: октябрь 2009 | Отправлено: 25 окт. 2009 18:07 | IP
|
|
Yukano Natsumi

Новичок
|
      
Все равно не могу понять принцип решения...Каким способом решается это:

|
Всего сообщений: 30 | Присоединился: октябрь 2009 | Отправлено: 31 окт. 2009 10:56 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Yukano Natsumi написал 31 окт. 2009 10:56
Все равно не могу понять принцип решения...Каким способом решается это:

^{n} - 1}{\frac{1}{2} - 1} }{1*\frac{(\frac{1}{3})^{n} - 1}{\frac{1}{3} - 1} } = )
^{n})}{\frac{3(1 - (\frac{1}{3})^{n})}{2} } = \frac{2*(1-0)}{\frac{3*(1-0)}{2} } = \frac{4}{3} )
(Сообщение отредактировал RKI 31 окт. 2009 11:57)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 31 окт. 2009 11:55 | IP
|
|
Yukano Natsumi

Новичок
|
      
RKI
Я не могу понять,что вы сделали(( Как вы упростили?
|
Всего сообщений: 30 | Присоединился: октябрь 2009 | Отправлено: 31 окт. 2009 12:04 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Yukano Natsumi написал 31 окт. 2009 12:04
RKI
Я не могу понять,что вы сделали(( Как вы упростили?
В числителе и в знаменателе стоят геометрические прогрессии. Просто воспользовалась формулой для суммы геометрической прогрессии
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 31 окт. 2009 13:45 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.1.1 Предел последовательности
2.1.1 Предел последовательности

 Форум
Форум

 Математика
Математика

 2.1.1 Предел последовательности
2.1.1 Предел последовательности