Форум - 1.25 Стереометрия [9]

Форум	» Назад на решение задач по физике и термеху
Регистрация \| Профиль \| Войти \| Забытый пароль \| Присутствующие \| Справка \| Поиск

» Добро пожаловать, Гость: Войти | Регистрация

	Форум Математика 1.25 Стереометрия
	Отметить все сообщения как прочитанные [ Помощь ] » Добро пожаловать на форум "Математика" «

Переход к теме
<< Назад Вперед >>

Несколько страниц [ 1 2 3 4 5 6 7 8 9 10 11 ]
Модераторы: Roman Osipov, RKI, attention, paradise

MEHT

Долгожитель

Ужас начинается тогда, когда актуатор уменьшится настолько, что ляжет в плоскость DEF. Он застревает в этом среднем положении: Дальше сокращаться он не может, потому что он уже предельно натянут. Математически - расширяться он тоже не может, потому что невозможно определить в какую сторону он повернёт плоскость DEF относительно своего стабильного ребра - по часовой стрелке или против. IRL мы знаем что гравитация из этого положения будет тянуть вниз, и при последующем увеличении актуатора угол продолжит уменьшаться, пока DEF не провалится под ABC.
Надо быть ещё уверенным, что такая "критическая длина" вообще реализуема. Допустим, что при максимуме фиксированных актуаторов это так.
Ну а если изменить эти фиксированные параметры? В таком случае уже не будет гарантии, что эта "критическая длина" тоже не изменится и не попадёт в допустимый интервал изменения длин актуаторов.. да и скорей всего попадёт. А это будет означать, что можно путём вариации длин переходить от одного положения плоскости в другое при том, что исходные длины восстаналвиваются (тот самый ответ "да" на поставленный постом выше ВОПРОС).

Хорошо было бы найти эту критическую длину. И сколько не саму длину, а факт того, попадает ли она в допустимый интервал изменения длин актуаторов. Её строгий расчёт напрямую невозможен - у нас нет аналитического выражения для x=x(a,b,c).

Если бы была известна явная зависимость x=x(a,b,c), где a,b - фиксированы, c - меняется, то для нахождения минимума (экстремума) x следовало бы взять производную от x по c, приравнять к нулю и выразить c. Но такой зависимости у нас нет. Даже если дифференцировать по "с" неявную зависимость икса от параметров g(x, a, b, c) = 0, то получим условие

$\frac{\partial g}{\partial c}=0,$

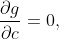
где будет зависимость от x, которую следует заменять на x(a,b,c) чтобы получить уравнение для выражения с через фиксированные параметры a и b.

Спасает снова графический метод - плавно меняя c при фиксированных a и b ищем при каких значениях c графики g1,g2,g3,g4 касаются оси абсцисс или же имеет место перегиб (касательная в точке пересечения совпадает с осью абсцисс). Я немного поколдовал в маткаде и получил, что при фиксированных максимальных a и b для c критическая длина будет находится в диапазоне допустимой длины актуатора (меняя c, графиком g3 удалось "коснуться" оси абсцисс). А значит плавным изменением актуаторов можно добиватся и двойственных решений.

Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 30 июня 2012 19:19 | IP

thunder87l

Новичок
"Косинус меняется от -1 до 1, проекция - от -a до a. Диапазон изменения углов при этом от нуля до 180°"

График приятнее выглядит. С разными а график получается разного размера и мне так не очень удобно. Диапазон изменения углов максимум - от 0° до 90°, потому что l по условию меньше L.

Всего сообщений: 29 | Присоединился: июнь 2012 | Отправлено: 30 июня 2012 23:43 | IP

thunder87l

Новичок
Честно говоря - слабо понял ))

"это будет означать, что можно путём вариации длин переходить от одного положения плоскости в другое при том, что исходные длины восстаналвиваются"

По идее мне надо менять актуаторы таким образом, чтобы платформа не переходила в свои "альтернативные" устойчивые состояния. Потому я и сказал про
AD∙[DE×DF]>0
BE∙[DE×DF]>0
CF∙[DE×DF]>0

По идее если эти ограничения выполняются, нет никакой возможности из изначального "правильного положения" вывернуть платформу куда не надо. Во всяком случае я не могу себе представить такой способ это сделать, чтобы хоть один из актуаторов не попал в плоскость платформы.

Хотя на самом деле там должно быть даже не >0, а больше какой-то пока неопределённой величины. Механизм не идеален - крепления будут иметь некоторую свободу, поэтому подходить вплотную к пределу не стоит, особенно - с нагрузкой на платформу.

Всего сообщений: 29 | Присоединился: июнь 2012 | Отправлено: 1 июля 2012 0:20 | IP

MEHT

Долгожитель

Диапазон изменения углов максимум - от 0° до 90°, потому что l по условию меньше L.
Из того, что l<L ещё не значит что углы не могут превышать 90°. Я же приводил решение, где были отрицательные проекции. Отрицательные проекции - отрицательный косинус - как следствие угол больше 90°.

"это будет означать, что можно путём вариации длин переходить от одного положения плоскости в другое при том, что исходные длины восстаналвиваются"

По идее мне надо менять актуаторы таким образом, чтобы платформа не переходила в свои "альтернативные" устойчивые состояния. Потому я и сказал про
AD∙[DE×DF]>0
BE∙[DE×DF]>0
CF∙[DE×DF]>0

По идее если эти ограничения выполняются, нет никакой возможности из изначального "правильного положения" вывернуть платформу куда не надо. Во всяком случае я не могу себе представить такой способ это сделать, чтобы хоть один из актуаторов не попал в плоскость платформы.
Непрерывные взаимопреобразования одних положений платформы в другие путём варьирования ножек актуатора возможны, но не для всех решений - не все графики при смене параметров будут "играть корнями". Для наглядности попробуйте построить сначала графики g1, g2, g3, g4 при максимальных a, b, c, а потом начать медленно уменьшать c. Вы заметите, что примерно
при c=210.4/120 начнёт исчезать второй корень g4,
при c=202.8/120 начнёт появлятся третий корень g2,
примерно при c=184.5/120 три корня g2 сольются в один (первый и третий стремятся ко второму, совпадающему со вторым корнем g1)

Исчезание корней можно трактовать как уход ножек актуатора под основание; сливание корней - ветвление решений.

Т.е. видно, что для решений, даваемых графиком функции g2 будет критическая точка c=184.5/120, при которой возможны ветвления - можно перескочить на решения g1. Однако я не проверял эти решения неравенствами, поэтому не исключены переходы в "инверсные" решения.

Ладно оставим эту математическую экзотику.
Всё оказалось много проще, чем я предполагал. Ключевую роль тут будет играть то, как Вы собираетесь конструировать своё устройство. Можно, предварительно установив ножки на минимум длины, получить два возможных варианта соединения их с платформой:

1) параллельно основанию: все ножки под углами 83°42'23" к основанию;
2) под углом к основанию: две ножки под углами 83°42'23", другая под 33°48'46" к основанию (строго говоря, математически этот второй случай будет описыватся тремя парами углов, т.к. наклонять платформу можно к любой из трёх ножек. По сути это будут три симметричных случая - можно рассматривать любой из них)

Логичнее предположить, что Вы предпочтёте 1-й случай конструирования. Тогда вглянув на решения даваемые графиками легко видеть, что описывает его меньший корень функции g4 (первый корень чёрного графика на графике-рисунке).
Меняя параметры легко проследить и эволюцию сего графика и его корней. При выбранных Вами параметрах он никогда не исчезает и не сливается с другими корнями, а значит исключены и "критические точки"; левый корень всегда существует (чего не скажешь о правом) - следовательно для каждой тройки параметров a, b, c будет однозначно найдены углы α, β, γ - именно те углы, которые будут реализовыватся устройством. Ну.. вроде как и всё. Можно строить таблицы.

Что до условий

(x - sqrt(3))∙y(x) + 1 - l² + a² + b² - x∙sqrt(3) ≥ 0 и
(x - sqrt(3))∙z(x) + 1 - l² + a² + c² - x∙sqrt(3) ≥ 0,

то раз они выполнялись для крайних положений актуаторов, то будут выполнены и для промежуточных стадий - нет смысла каждый раз проверять. Условия с векторными произведениями оказались не нужны.

Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 1 июля 2012 17:26 | IP

thunder87l

Новичок
ОК, спасибо огромное. Finally ))

"1) параллельно основанию: все ножки под углами 83°42'23" к основанию;
2) под углом к основанию: две ножки под углами 83°42'23", другая под 33°48'46" к основанию"
Вы правильно предположили, в моём случае нужен именно первый вариант, хотя я вполне представляю где в роботике можно было бы использовать второй. Это хорошая инфа, возможно когда-нибудь пригодится ))

И ещё раз - огромное спасибо. Я себе всю голову сломал на этом ))

Всего сообщений: 29 | Присоединился: июнь 2012 | Отправлено: 1 июля 2012 18:49 | IP

MEHT

Долгожитель
Рад был помочь Я тоже и не предполагал, что решение так надолго затянется..

Но всё же в довесок для сверки приведу ещё несколько численных расчётов для разных параметров. А предварительно хорошо бы ещё найти угол наклона платформы к основанию. Его косинус даётся скалярным произведением векторов нормали к основанию n и вектора нормали к подвижной платформе s, даваемому выражением

$\vec{s} = \frac{ \left [ \vec{DE}\times \vec{DF} \right ] }{\left | \left [ \vec{DE}\times \vec{DF} \right ]\right |}=\frac{ \left [ \vec{DE}\times \vec{DF} \right ] }{l^2\sin\frac{2\pi}{3}}=\\\\\\ =\frac{ \left [ \left (\left (\frac{1}{\sqrt{3}} - x \right ) \vec{\tau}_1 - \left (\frac{1}{\sqrt{3}} - y \right ) \vec{\tau}_2 + \left (\sqrt{a^2-x^2} - \sqrt{b^2-y^2} \right ) \vec{n} \right ) \times \left (\left (\frac{1}{\sqrt{3}} - x \right ) \vec{\tau}_1 - \left (\frac{1}{\sqrt{3}} - z \right ) \vec{\tau}_3 + \left (\sqrt{a^2-x^2} - \sqrt{c^2-z^2} \right ) \vec{n} \right ) \right ] }{\left (\frac{l}{L} \right )^2\cdot \frac{\sqrt{3}}{2}}.$

Тут для векторно перемножаемых векторов были использованы соотношения, выражающие их через проекции:

$\vec{DE}=\left (\frac{L}{\sqrt{3}} - a\cos\alpha \right ) \vec{\tau}_1 - \left (\frac{L}{\sqrt{3}} - b\cos\beta \right ) \vec{\tau}_2 + \left (a\sin\alpha - b\sin\beta \right ) \vec{n}=\\\\ = L\cdot \left (\left (\frac{1}{\sqrt{3}} - x \right ) \vec{\tau}_1 - \left (\frac{1}{\sqrt{3}} - y \right ) \vec{\tau}_2 + \left (\sqrt{a^2-x^2} - \sqrt{b^2-y^2} \right ) \vec{n} \right ),\\\\\\ \vec{DF}= L\cdot \left (\left (\frac{1}{\sqrt{3}} - x \right ) \vec{\tau}_1 - \left (\frac{1}{\sqrt{3}} - z \right ) \vec{\tau}_3 + \left (\sqrt{a^2-x^2} - \sqrt{c^2-z^2} \right ) \vec{n} \right ).$

(Тут есть небольшая путаница с размерными и безразмерными параметрами - слева стоят размерные a, b, справа - безразмерные; однако на конечном результате это не скажется)

Тогда искомый косинус будет

$\cos\theta =\vec{s}\,\vec{n}$

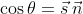
и после раскрытия скобок в векторном произведении s, и учтя что

$\left [\vec{\tau}_1\,\vec{\tau}_2 \right ]=\left [\vec{\tau}_2\,\vec{\tau}_3 \right ]=\left [\vec{\tau}_3\,\vec{\tau}_1 \right ]=\frac{\sqrt{3}}{2}\,\vec{n},$

окончательно получим

$\cos\theta = \frac{\left ( \frac{\sqrt{3}}{3}-x \right )\left ( \frac{\sqrt{3}}{3}-y \right )+\left ( \frac{\sqrt{3}}{3}-y \right )\left ( \frac{\sqrt{3}}{3}-z \right ) +\left ( \frac{\sqrt{3}}{3}-z \right )\left ( \frac{\sqrt{3}}{3}-x \right )}{l^2},$

где l - безразмерный параметр.

А теперь некоторые результаты.

Повторюсь, что
при минимальных длинах a=b=c=158/120 будет α = β = γ ≈ 83°42'23" ,
при максимальных a=b=c=218/120 будет α = β = γ ≈ 85°26'35" ,
в обоих этих случаях угол наклона θ будет равен нулю (плоскости треугольников параллельны).

При a=b=158/120, c=198/120

α ≈ 83°42'23" ,
β ≈ 83°42'23" ,
γ ≈ 81°56'09" ,
θ ≈ 30°02'11" ;

при a=158/120, b=178/120, c=198/120

α ≈ 81°35'39" ,
β ≈ 85°18'28" ,
γ ≈ 83°26'40" ,
θ ≈ 26°41'02" ;

при a=158/120, b=c=198/120

α ≈ 79°11'24" ,
β ≈ 84°58'53" ,
γ ≈ 84°58'53" ,
θ ≈ 32°38'43" ;

при a=158/120, b=198/120, c=218/120

α ≈ 75°50'41" ,
β ≈ 86°48'47" ,
γ ≈ 83°04'26" ,
θ ≈ 46°10'42" ,

ну и так далее..

(Сообщение отредактировал MEHT 4 июля 2012 1:22)

Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 3 июля 2012 3:02 | IP

thunder87l

Новичок
Здравствуйте, это снова я ))

Это смешно, но у меня не получается численно решить систему.

Здесь находится pdfка описывающая решение:
внешняя ссылка удалена

Решал по вашим гайдлайнам, но немного по-своему. Немного увлёкся с субституциями 1) чтобы формулы на лист влезали, 2) чтобы самому не шугаться своих записей.

Всего сообщений: 29 | Присоединился: июнь 2012 | Отправлено: 14 июля 2012 0:10 | IP

thunder87l

Новичок
В документе всё описывается до x=f(y), z=f(y).
Дальше я написал программу для матлаба:

clear all;

%define actuator lenghts [a,b,c], base length [L], platform length [l], and constant D
syms a b c l L D;

%define related parameters
a0=a/L; b0=b/L; c0=c/L; l0=l/L; D=-2*sqrt(3);
Nab=1+a0^2+b0^2-l0^2; Nbc=1+b0^2+c0^2-l0^2; Nca=1+c0^2+a0^2-l0^2;
Eb=4*b0^2+3; Ea=4*a0^2+3; Ec=4*c0^2+3;
Fab=2*Nab+6; Fbc=2*Nbc+6; Fca=2*Nca+6;
Gca=Nca^2-4*c0^2*a0^2;
Ja=a0^2+1; Jc=c0^2+1;
Kb=1+b0^2+l0^2;
Lab=Nab^2-7*a0^2*b0^2-3*a0^2-3*b0^2; Lbc=Nbc^2-7*b0^2*c0^2-3*b0^2-3*c0^2;
MBa=Nab^2-4*a0^2*b0^2-3*a0^2; MBc=Nbc^2-4*c0^2*b0^2-3*c0^2;

%define x,y,z, x=a0*cos(alpha)
syms x y z;

%define x=F(y) and z=F(y)
x=(-D*y^2-Fab*y-D*Nab-4*sqrt(3*Ja*y^4 +D*Kb*y^3 +Lab*y^2 -D*Kb*b0^2*y -b0^2*MBa))/(-6*y^2+2*D*y+2*Eb);
z=(-D*y^2-Fbc*y-D*Nbc-4*sqrt(3*Jc*y^4 +D*Kb*y^3 +Lbc*y^2 -D*Kb*b0^2*y -b0^2*MBc))/(-6*y^2+2*D*y+2*Eb);

%define F(x,y,z)=0
F=-3*z^2*x^2+D*z^2*x+D*z*x^2+Ea*z^2+Ec*x^2+Fca*x*z+D*Nca*z+D*Nca*x+Gca;

%substitute l and L with real values
len_l=90; len_L=120;
F=subs(F,{l,L},{len_l,len_L});

%substitute actuator lengths with real values
len_a=218; len_b=218; len_c=218;
Y=subs(F,{a,b,c},{len_a,len_b,len_c});

%solving to get y, x, z
y0=solve(Y,y);
x0=double(subs(x,{a,b,c,l,L,y},{len_a,len_b,len_c,len_l,len_L,y0}));
z0=double(subs(z,{a,b,c,l,L,y},{len_a,len_b,len_c,len_l,len_L,y0}));

%expressing angles
alpha=double(acos(x0/(len_a/len_L)))/pi*180
beta=double(acos(y0/(len_b/len_L)))/pi*180
gamma=double(acos(z0/(len_c/len_L)))/pi*180

Здесь я сперва использую символьную библиотеку для того чтобы составить x=f(y), z=f(y), затем подставить их в F(x,z)=0.

Затем вместо абстрактных символов подставляются численные значения a, b, c, l, L. Полученое выражение тогда решается матлабом через solve. z,x использую вторые (с минусом перед корнем), как по идее следует из поста.

Потом, получив y выражаю x и z. И получается полная фигня...

Всего сообщений: 29 | Присоединился: июнь 2012 | Отправлено: 14 июля 2012 0:11 | IP

thunder87l

Новичок
Например, для сравнения с вашими результатами:

a=b=c=158, ваш: α = β = γ ≈ 83°42'23" = 83.7063889°
мой: α = γ = 83.706389339979239°
β = 85.184961122165504°

a=b=c=218, ваш: α = β = γ ≈ 85°26'35" = 85.4430556°
мой: α = γ = 85.442939979311305°
β = 86.162348797033317°

a=b=158, c=198
ваш:
α = β ≈ 83°42'23" = 83.7063889°
γ ≈ 81°56'09" = 81.9358333°
мой:
α = 83.777410144223822°
β = 85.132007060922746°
γ = 81.882340260223359°

a=158, b=198, c=218
ваш:
α ≈ 75°50'41" = 75.8447222°,
β ≈ 86°48'47" = 86.8130556°,
γ ≈ 83°04'26" = 83.0738889°
мой:
α = 76.102364221694728°
β = 87.423319326652887°
γ = 82.972696045379109°

Как видите - получается не очень, но даёт ответы очень близкие к правильным. Не похоже на совпадение. 'y' как-то стрёмно находится. всё время немного выше чем должен быть, но при подстановке в выражение для x, z вроде даёт всё правильно. У меня есть смутные сомнения насчёт косинусов и квадратов..

Всего сообщений: 29 | Присоединился: июнь 2012 | Отправлено: 14 июля 2012 0:11 | IP

thunder87l

Новичок
Что ещё интересного?.. Вычисления с помощью solve жрут очень много времени (150 сек в среднем, ибо компу уже 7 годиков), поэтому я попробовал заменить на алгоритм бинарного поиска - оказалось раз в 5-8 быстрее, с приемлемой точностью. Но тем не менее, даже 10 секунд на нахождение решения при 13 возможных позициях актуатора - это больше 6 часов вычислений с полной загрузкой процессора.

Поэтому я вспомнил школьную комбинаторику чтобы отбросить дублирующиеся позиции. Количество рассчётов уменьшилось до 20% от возможных, что выглядит уже чуть более по-божески.

Всего сообщений: 29 | Присоединился: июнь 2012 | Отправлено: 14 июля 2012 0:17 | IP

Отправка ответа:

Имя пользователя Вы зарегистрировались?
Пароль Забыли пароль?
Сообщение
Использование HTML запрещено
Использование IkonCode разрешено
Смайлики разрешены

Опции отправки
Добавить подпись?
Получать ответы по e-mail?
Разрешить смайлики в этом сообщении?
Просмотреть сообщение перед отправкой? Да Нет

Переход к теме
<< Назад Вперед >> Несколько страниц [ 1 2 3 4 5 6 7 8 9 10 11 ]