Форум     Математика         1.25 Стереометрия
	Отметить все сообщения как прочитанные   [ Помощь ] » Добро пожаловать на форум "Математика" «

Переход к теме << Назад Вперед >> Несколько страниц [ 1 2 3 4 5 6 7 8 9 10 11 ] Модераторы: Roman Osipov, RKI, attention, paradise

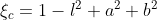
MEHT Долгожитель Введём две вспомогательные функции трёх переменных: и тут понятно, что для удобства записи индекс обозначает отсутствующий квадрат параметра в сумме справа, я не стал расписывать явно в f. Через них y и z предстанут так функции x и соответствующих параметров: Подставляем их в исходное уравнение или в квадратное уравнение, получаемое из него возведением в квадрат (при этом дополнительно придётся приписать к нему и ограничивающие неравенства): и ещё два неравенства, ответственные за вещественность y и z (положительность дискриминантов), но не выписываю (их можно предварительно наложить на f, потребовав её вещественности). Существует нерадужная перспектива вновь избавится от радикалов в последнем уравнении, при этом два раза придётся возводить уравнение в квадрат до этого соответствующим образом преобразовав. При каждом таком возведении будут появлятся дополнительные неравенства-ограничения. В конечном итоге всё сведётся к некоторому алгебраическому уравнению n-й степени (без радикалов), которое будет разрешатся численно. Ну а раз численного решения не избежать, то лучше уж будем отталкиватся от исходного. Подставляем в него различные комбинации наших функций. Всего возможны 4 комбинации чередования знаков: ++, +-, -+, --, соответственно будет и 4 уравнения: Для решения строим 4 графика функций g(x), потом ищем их нули на отрезке -a≤x≤a. (Я строил в маткаде). Лишние иксы впоследствии отметаются неравенствами наложенными на y и z (фактически же - на f), само уравнение мы не преобразовывали, следовательно на него ничего не накладываем (эти неравенства по сути содержатся уже в самих уравнениях). Каждому иксу будет отвечать по два игрека, находим их, лишнее отсееваем неравенствами. Ну и для z аналогично. Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 24 июня 2012 17:52 | IP thunder87l Новичок Омг, ужас. Я тоже вытащил корни x1, x2, z1, z2 и подставил в третье уравнение. Результат оказался довольно страшным, и выражать оттуда y я не решился. В какой-то момент мне пришла в голову мысль, что считать эти чудесные функции на микроконтроллере будет не слишком классно. Другой чувак, который этот контроллер будет програмить сказал что по его подсчётам на конкретном таймере мы сможем генерировать PWM только для 12-13 позиций актуатора. Затем пришла в голову идея, что 3 параметра по 12 возможных значений - не такая большая таблица, и по идее можно просто запустить матлаб считать по готовой формуле положения и затем использовать уже готовенькое. Позднее пришла в голову мысль получше, что когда будет добыта таблица, в принципе можно попробовать подобрать похожую функцию, которая с ошибкой до 5% будет апроксимировать настоящую. Посмотрим что у меня получится )) Всего сообщений: 29 | Присоединился: июнь 2012 | Отправлено: 24 июня 2012 23:52 | IP thunder87l Новичок Я кстати определился с размерами. L=120mm, l=90mm, a,b,c=158+[0..60]. Это я вручную кое что прикинул. По идее должно бы давать наклон верхней плоскости около 45 градусов в случае когда один из актуаторов на максимум, а два других - на минимум. Достаточно широкая ножка (L) чтобы не сломало ветром, достаточно широкая верхняя платформа чтобы на неё закрепить то что нужно. Всего сообщений: 29 | Присоединился: июнь 2012 | Отправлено: 26 июня 2012 0:40 | IP MEHT Долгожитель Цитата: thunder87l написал 24 июня 2012 23:52 Затем пришла в голову идея, что 3 параметра по 12 возможных значений - не такая большая таблица, и по идее можно просто запустить матлаб считать по готовой формуле положения и затем использовать уже готовенькое. Позднее пришла в голову мысль получше, что когда будет добыта таблица, в принципе можно попробовать подобрать похожую функцию, которая с ошибкой до 5% будет апроксимировать настоящую. Посмотрим что у меня получится )) Про таблицы идея хорошая, но и тут будут подводные камни: как я уже говорил, при определённых параметрах задача может как иметь решение (в том числе возможны случаи нескольких решений), так и не иметь его. Это следует каким-то образом учесть при построении. Цитата: thunder87l написал 26 июня 2012 0:40 Я кстати определился с размерами. L=120mm, l=90mm, a,b,c=158+[0..60]. Это я вручную кое что прикинул. По идее должно бы давать наклон верхней плоскости около 45 градусов в случае когда один из актуаторов на максимум, а два других - на минимум. Достаточно широкая ножка (L) чтобы не сломало ветром, достаточно широкая верхняя платформа чтобы на неё закрепить то что нужно. Я численно прорешал такую систему в маткаде, взяв a и b минимальными (безразмерные длины соответствуют безразмерному 158/120), c - максимальным (т.е. безразмерное 218/120). И получил аж 6 различных решений! Все они удовлетворяют системе, а значит и должны реализовываться Вашим устройством. В этом и проявляются сюрпризы многопараметричного решения. Находил по вышеописанной схеме. Строим графики g1(x), g2(x), g3(x), g4(x): тут g1(x) - красный, g2(x) - синий, g3(x) - фиолетовый, g4(x) - чёрный. Красный график не пересекает ось иксов на отрезке [-a;a], следовательно корней не даёт. (Вот если бы мы подставляли y(x) и z(x) не в исходное, а в возведённое в квадрат уравнение, то корни бы были, но они всё равно были бы отброшенны как неудовлетворяющие некоторому неравенству). Синий график даёт один корень: x1 ≈ -0.2094625659739, ему отвечают y1 = f+(x1,a,b) ≈ 0.8366190511315 и z1 = f-(x1,a,c) ≈ 0.8679499046817; фиолетовый график - 4 корня: x2 ≈-0.1509056720145, ему отвечают y2 = f-(x2,a,b) ≈ 0.5514736625068 и z2 = f+(x2,a,c) ≈ 1.3392776698929; x3 ≈ 0.1443375672974, ему отвечают y3 = f-(x3,a,b) ≈ 0.1443375672974 и z3 = f+(x3,a,c) ≈ 1.4193891544230; x4 ≈ 0.5514736625068, ему отвечает y4 = f-(x4,a,b) ≈-0.1509056720145 и z4 = f+(x4,a,c) ≈ 1.3392776698929; x5 ≈ 0.8366190511315, ему отвечают y5 = f-(x5,a,b) ≈-0.2094625659739 и z5 = f+(x5,a,с) ≈ 0.8679499046817; чёрный график - один корень: x6 ≈ 0.1443375672974, ему отвечают y6 = f-(x6,a,b) ≈ 0.1443375672974 и z6 = f-(x6,a,с) ≈ 0.3497353470373. Условия (x - sqrt(3))∙y(x) + 1 - l² + a² + b² - x∙sqrt(3) ≥ 0 и (x - sqrt(3))∙z(x) + 1 - l² + a² + c² - x∙sqrt(3) ≥ 0 удовлетворяются всеми шестью решениями, т.е. никаких лишних решений не появилось. Теперь несложно выписать и углы (пишу сразу в градусах): α1 = β5 ≈ 99°09'14" , β1 = α5 ≈ 51°25'23" , γ1 = γ5 ≈ 61°27'36" ; α2 = β4 ≈ 96°34'53" , β2 = α4 ≈ 65°43'48" , γ2 = γ4 ≈ 42°30'18" ; α3 = α6 = β3 = β6 ≈ 83°42'23" , γ3 ≈ 38°37'08" , γ6 ≈ 78°54'02" . Отсюда при желании можно выразить и угол между нормалями подвижной и неподвижной плоскостей (по сути это и будет угол наклона верхней плоскости к нижней). (Сообщение отредактировал MEHT 26 июня 2012 22:30) Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 26 июня 2012 22:19 | IP MEHT Долгожитель Ещё забыл написать, что помимо условий (x - sqrt(3))∙y(x) + 1 - l² + a² + b² - x∙sqrt(3) ≥ 0 и (x - sqrt(3))∙z(x) + 1 - l² + a² + c² - x∙sqrt(3) ≥ 0 проверять следует также и -b ≤ y(x) ≤ b, -c ≤ z(x) ≤ c. Ну они, очевидно, выполнены (ведь удалось найти углы). (Сообщение отредактировал MEHT 27 июня 2012 0:56) Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 27 июня 2012 0:45 | IP MEHT Долгожитель Выявил ещё одну неточность в ходе общего построения. В самом начале при составлении системы я писал: (можно также считать что L>l, в противном случае конструкцию следует перевернуть и поменять местами L и l - снова будет L>l) А ведь ничего не выйдет Перевёрнутая конструкция не тождественна исходной при переобозначении L ↔ l - разный характер соединения рёбер с вершинами. Поэтому верхнее ограничение безразмерного параметра l единицей следует убрать. Всюду где было - поправляю. Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 27 июня 2012 14:39 | IP MEHT Долгожитель Только что прорешал систему когда все актуаторы установлены на минимум, т.е. a=b=c=158/120 и получил такие данные: 1) все рёбра составляют с плоскостью угол в 39°52'56", либо одно из рёбер вывернуто на угол 93°50'00", остальные же два так и будут фиксированы в положении на 39°52'56"; 2) все рёбра составляют с плоскостью угол в 83°42'23", либо одно из рёбер установлено на 33°48'46", остальные же два так и останутся на 83°42'23". Мне это показалось странным, ведь по сути мы получили два решения с плоскостями-платформами параллельными основаниям. И тут осенило, что вектора (геометрические длины, ориентированные относительно основания) в отличие от актуаторов могут самопересекатся! (пардон, без рисунка; но надеюсь Вы поймёте о чем речь). Эту вольность немедленно следует пресечь как и случай с самопересекающимися плоскостями основания и платформы. Каким образом это сделать? Сразу приходит на ум такая схема: Если треугольник-основание АВС обходится в некотором направлении (вид сверху), то в этом же направлении должен обходится и треугольник-платформа DEF. Это означает, что векторное произведение [AB×AC] (этот вектор коллинеарен нормали плоскости-основания) ориентирован также как и вектор [DE×DF] (термин "ориентирован" тут не в смысле совпадения направления). Математически это можно записать как положительность их скалярного произведения: [AB×AC]∙[DE×DF]>0. В продолжении мысли: Если треугольник АВС обходится против часовой стрелки, то [AB×AC] сонаправлен с нормалью n введённой ранее. Тогда условие такое: n∙[DE×DF]>0. В смешанном произведении можно производить циклическую перестановку векторов: DF∙[n×DE]>0. Тогда проще расписывать по компонентам. --- Что ж.. ещё одно ограничение на решения.. Меня не перестаёт удивлять эта задача... Надеюсь, что теперь всё окончательно прояснится. Однако даже щас интуиция мне подсказывает, что это условие не избавит от двойственности в некоторых решениях. 6 решений, конечно, перебор.. а вот половина из них вплоне может остатся. (Сообщение отредактировал MEHT 28 июня 2012 0:19) Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 27 июня 2012 23:35 | IP MEHT Долгожитель Или даже много проще - самопересечения рёбер будут тогда, когда любая из двух безразмерных проекций x, y, z некоторого найденного решения пересечёт центр треугольника-основания - точку О. Фактически это будет когда две из трёх безразмерных длин превысят значение в sqrt(3)/3 ≈ 0.57735 На основании этого критерия из первого решения сразу можно отмести 1-е и 5-е вчерашнего решения и решения: 1) все рёбра составляют с плоскостью угол в 39°52'56", либо одно из рёбер вывернуто на угол 93°50'00", остальные же два так и будут фиксированы в положении на 39°52'56" для случая актуаторов минимальных длин. --- Но всё-таки условие [AB×AC]∙[DE×DF]>0 в этом плане будет строже. Оно способно отбросить не только "пересечения актуаторов", но и случай "перевёрнутой" платформы вообще. (Сообщение отредактировал MEHT 28 июня 2012 1:14) Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 28 июня 2012 1:02 | IP thunder87l Новичок Для двух паралельных плоскостей есть 4 решения - плоскость DEF сверху и снизу от ABC, затем один случай - для пересекающихся векторов, второй - для непересекающихся. Но это только в случае с паралельными. Есть ещё вариант - углы альфа и бета - положительные, а гамма - отрицательный (и наоборот). Тоесть - DEF пересекается с ABC. При определённых обстоятельствах - это вполне получается, несмотря на то, что все актуаторы будут так-же одинаковой длинны. Я вообще искал не x, а выразил косинус - удобно для графического анализа поскольку косинус всегда между -1 и 1. Для симуляции я брал углы от 45 до 90 градусов, что несколько ускоряет процесс. [AB×AC]∙[DE×DF]>0 Смысл, как я понимаю - получить две нормали и пробить - в одну ли они смотрят сторону, так? Когда одну из плоскостей заломит на 90+ градусов относительно другой - скалярное произведение будет не больше нуля. Это очень хороший критерий (я бы не додумался), но тут пожалуй надо вместо нуля другой коэфициент поставить. Я по природе - визуал, поэтому дальнейшее моё объяснение - ужасный ужас. Уж извините )) Представьте эту треногу в исходном положении - все три актуатора на максимуме. Затем один из них начинает уменьшаться. Два других сохраняют положение, поскольку они удерживаются общим ребром сверху. Противолежащий этому ребру угол медленно ползёт вниз. Ужас начинается тогда, когда актуатор уменьшится настолько, что ляжет в плоскость DEF. Он застревает в этом среднем положении: Дальше сокращаться он не может, потому что он уже предельно натянут. Математически - расширяться он тоже не может, потому что невозможно определить в какую сторону он повернёт плоскость DEF относительно своего стабильного ребра - по часовой стрелке или против. IRL мы знаем что гравитация из этого положения будет тянуть вниз, и при последующем увеличении актуатора угол продолжит уменьшаться, пока DEF не провалится под ABC. Я это к тому, что существует это запретное положение, до которого нельзя скатываться, потому что в системе на физическом уровне появляется неопределённость. Сперва я думал решать это итеративно - поставить систему в определённое известное состояние и начать по очереди уменьшать/увеличивать значения актуаторов выбирая при этом самый близкий корень до тех пор, пока не наткнусь на это положение (если с моими актуаторами оно вообще возможно). А вот теперь посмотрел на ваш критерий и подумал, что когда нормали ABC и DEF ещё не перпендикулярны, но уже близко к тому - это для моей системы 100% сигнализирует о том, что один из актуаторов вывернут наизнанку (меньше 40-45 градусов этот угол быть по идее не может). Там два способа включить это в рассчёт - или высчитать этот коэфициент каким-то хитрым образом, или детектить когда один или больше актуаторов попадает в плоскость DEF и проваливается под неё. Можно использовать ваш же критерий - проверить скалярное умножение вектора актуатора и нормали DEF. Если я всё правильно придумал, должна получиться система: [AB×AC]∙[DE×DF]>0 AD∙[DE×DF]>0 BE∙[DE×DF]>0 CF∙[DE×DF]>0 Всего сообщений: 29 | Присоединился: июнь 2012 | Отправлено: 28 июня 2012 4:41 | IP MEHT Долгожитель Для двух паралельных плоскостей есть 4 решения - плоскость DEF сверху и снизу от ABC, затем один случай - для пересекающихся векторов, второй - для непересекающихся. Решения с отрицательными углами можно вообще не рассматривать - они будут повторять все решения в положительных углах (как если бы верхняя картинка зеркально отражалась в плоскости-основании). Но это только в случае с паралельными. Есть ещё вариант - углы альфа и бета - положительные, а гамма - отрицательный (и наоборот). Тоесть - DEF пересекается с ABC. При определённых обстоятельствах - это вполне получается, несмотря на то, что все актуаторы будут так-же одинаковой длинны. Тут можете быть спокойным - пересечений не будет. Для этого и были записаны условия (x - sqrt(3))∙y(x) + 1 - l² + a² + b² - x∙sqrt(3) ≥ 0 и (x - sqrt(3))∙z(x) + 1 - l² + a² + c² - x∙sqrt(3) ≥ 0, а поскольку он и выполнены, то пересечений не будет и гамму следует брать положительной. Я вообще искал не x, а выразил косинус - удобно для графического анализа поскольку косинус всегда между -1 и 1. Для симуляции я брал углы от 45 до 90 градусов, что несколько ускоряет процесс. Так x и косинус это одно и то же с точностью до множителя a (безразмерного). Косинус меняется от -1 до 1, проекция - от -a до a. Диапазон изменения углов при этом от нуля до 180° (углы положительны). Когда мы от уравнения с тригонометрией переходим к уравнению в проекциях заметьте, - произведение синусов заменяется на произведение радикалов и взято со знаком "+". Это означает что оба синуса в произведении будут одного знака (оба положительны или оба отрицательны), то же можно сказать и об углах. Геометрически же это будет означать, что точки D и E лежат по одну сторону от плоскости-основания ABC, что исключает пересечение ребра DE с плоскостью ABC. (И для двух других уравнений также.) Но когда мы возводим уравнение в квадрат теряется знак при радикалах, поэтому и нужно накладывать условие (x - sqrt(3))∙y(x) + 1 - l² + a² + b² - x∙sqrt(3) ≥ 0 выбрасывающее решения со знаком "-" у радикалов, если таковы имели место появится. Почему же тогда не писать и (y - sqrt(3))∙z + 1 - l² + b² + c² - y∙sqrt(3) ≥ 0 ? Да потому, что уравнение связывающее y и z в квадрат не возводилось, следовательно и так уже содержит в себе это условие. [AB×AC]∙[DE×DF]>0 Смысл, как я понимаю - получить две нормали и пробить - в одну ли они смотрят сторону, так? Когда одну из плоскостей заломит на 90+ градусов относительно другой - скалярное произведение будет не больше нуля. Это очень хороший критерий (я бы не додумался), но тут пожалуй надо вместо нуля другой коэфициент поставить. Да, на это и был расчёт. Ведь фактически при [AB×AC]∙[DE×DF]<0 платформа будет перевёрнута - "верхняя" и "нижняя" стороны её поверхности поменяются местами. Конечно можно выбрать и другой ограничивающий параметр, как Вы предлагаете, - тогда платформе будет "разрешено" отклонятся от горизонтального положения не больше чем на некоторый максимальный угол. Но всё же такой подход мне кажется черезчур искусственным. Объясню почему я так считаю. Изначально ставилась такая задача: по набору длин актуаторов определить положение плоскости. Эта задача, хоть и не аналитически, а численно, но разрешима. Плавно меняя параметры мы тем самым плавно меняем и положение платформы. Известно также, что одному и тому же набору параметров могут соответствовать разные устойчивые положения платформы. Именно УСТОЙЧИВЫЕ, иначе при фиксированных длинах актуаторов мы бы имели не дискретные наборы углов-решений, а некоторый непрерывный диапазон их изменений. Отсюда ВОПРОС: можно каким-нибудь образом, от некоторого фиксированного положения платформы (характеризуемой некоторыми длинами актуаторов) путём плавного их изменения в конечном итоге придти к некоторому другому положению платформы, при том, чтоб сами длины актуаторов опять бы стали исходными (т.е. поменялись только углы)? Если ответ "да", то оба решения справедливы, и Ваши ограничения AD∙[DE×DF]>0 BE∙[DE×DF]>0 CF∙[DE×DF]>0 вроде как становятся лишними, т.к. "запрещают" возможные решения. А ведь скорей всего ответ на этот вопрос и звучит "да" (об этом ниже). Меня терзают смутные сомнения и по поводу [AB×AC]∙[DE×DF]>0 запрещающему "переворот" плоскости-платформы. Просто мысленно я не могу представить себе ситуации, когда при непрерывном измененении длин актуаторов такой переворот имел бы место. Но главное, почему я записал это условие - это его способность пресечь явные "инверсии" плоскости, нереализуемые никаким плавным изменением параметров. Для наклядности представьте, что верхняя платформа способна "иногда" деформироватся (скажем, иногда - в процессе смены положения - она резиновая). Зафиксировав актуаторы в некоторых положениях мы бы с лёгкостью, путём деформации платформы, могли бы перехоидть от одного устойчивого положения в другое не меняя длин. Однако же ни при какой деформации платформы мы не перейдём от к решению хотя из уравнений оно и следует. Это сродни "инверсии" плоскости - когда чтоб принять такое положение резиновой плоскости следует стянутся в точку, а потом из точки вновь "вывернутся" в платформу. Такие ситуации как раз и будут пресекатся условием [AB×AC]∙[DE×DF]>0. (Сообщение отредактировал MEHT 30 июня 2012 19:23) Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 30 июня 2012 18:52 | IP

Отправка ответа: Имя пользователя   Вы зарегистрировались? Пароль   Забыли пароль? Сообщение Использование HTML запрещено Использование IkonCode разрешено Смайлики разрешены Опции отправки Добавить подпись? Получать ответы по e-mail? Разрешить смайлики в этом сообщении? Просмотреть сообщение перед отправкой? Да   Нет

Переход к теме << Назад Вперед >> Несколько страниц [ 1 2 3 4 5 6 7 8 9 10 11 ] Перейти к --   О сайте Замечания и предложения --   Тематические Информационные технологии Книги и решебники Математика Физика Экономика

Форум работает на скрипте © Ikonboard.com