ctarik

Новичок
|
      
не могу перевести в сферические координаты
|
Всего сообщений: 9 | Присоединился: октябрь 2011 | Отправлено: 5 апр. 2012 17:39 | IP
|
|
MEHT


Долгожитель
|
     
Проекцией полусферы S на YOZ будет круг
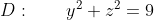
x через y,z выразится как
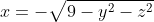
Исходный поверхностный интеграл сводится к двойному интегралу по D:
%5C,dz%5C,dy%20=%20-%5Ciint%5Climits_{D}%20%5Cleft%20(2-%5Csqrt{9-y^2-z^2}%20%5Cright%20)%5C,dz%5C,dy)
(знак у интеграла справа выбран согласно выбору внутренней стороны поверхности S)
Теперь сводите его к двухкратному, переходя к полярным координатам в YOZ.
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 5 апр. 2012 19:15 | IP
|
|
Dim

Новичок
|
     
Помогите,пожалуйста, с задачей:
Вычислить объем тела, заданного ограничивающими его поверхностями:
x^2+y^2=2*y*2^(1/2)
-z=x^2+y^2-16
z>=0
|
Всего сообщений: 42 | Присоединился: январь 2012 | Отправлено: 8 апр. 2012 10:12 | IP
|
|
lilymurlyka


Начинающий
|
      
Скажите, пожалуйста, как строить график у этой задачи?
Вычислить с помощью двойного интегралав полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а>0).(x^2+y^2)^2=a^2(4x^2+y^2)
Я просто не понимаю. Знаю, что лемниската, а по каким критериям её строить?
|
Всего сообщений: 70 | Присоединился: ноябрь 2011 | Отправлено: 12 апр. 2012 17:02 | IP
|
|
ustam


Долгожитель
|
      
lilymurlyka Нет, это не лемниската. В уравнении лемнискаты во 2-ой скобке должно быть (x^2 - y^2).Если перейти к полярным координатам, то получается (r - это "ро", а f - это "фи"):
r^2 = a^2[3(cosf)^2 + 1]
Форма кривой похожа на эллипс, но уравнение эллипса в полярных координатах совсем другое.
Очень похоже, что вы неправильно списали условие.
|
Всего сообщений: 420 | Присоединился: декабрь 2008 | Отправлено: 12 апр. 2012 18:05 | IP
|
|
lilymurlyka


Начинающий
|
      
Если не ошибаюсь, это должен быть эллипс?
|
Всего сообщений: 70 | Присоединился: ноябрь 2011 | Отправлено: 12 апр. 2012 18:05 | IP
|
|
lilymurlyka


Начинающий
|
      
Нет, условие я сейчас проверила еще раз. Оно правильно списано.
|
Всего сообщений: 70 | Присоединился: ноябрь 2011 | Отправлено: 12 апр. 2012 18:11 | IP
|
|
lilymurlyka


Начинающий
|
      
Я тогда совсем зависла(((
|
Всего сообщений: 70 | Присоединился: ноябрь 2011 | Отправлено: 12 апр. 2012 18:15 | IP
|
|
lilymurlyka


Начинающий
|
      
Помогите, пожалуйста, составить.
|
Всего сообщений: 70 | Присоединился: ноябрь 2011 | Отправлено: 12 апр. 2012 18:21 | IP
|
|
ustam


Долгожитель
|
      
lilymurlyka Я же написал, что это не эллипс, а только похож. Как и эллипс, фигура симметрична относительно осей координат. Поэтому для нахождения площади достаточно найти площадь четвертинки и умножить на 4.
Посмотрите, как пишется и решается двойной интеграл в полярных координатах. Площадь четвертинки находите интегрированием: r меняется в пределах от 0 до а*корень из [3(cosf)^2 + 1], f меняется от 0 до пи/2
|
Всего сообщений: 420 | Присоединился: декабрь 2008 | Отправлено: 12 апр. 2012 18:41 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.1.10 Криволинейные интегралы
2.1.10 Криволинейные интегралы

 Форум
Форум

 Математика
Математика

 2.1.10 Криволинейные интегралы
2.1.10 Криволинейные интегралы