thunder87l


Новичок
|
     
Решение:
Выражение вектора DE состоит из 6 членов, по порядку - a, b, c, d, e, f. Значит при возведении в квадрат, учитывая скалярное произведение векторов должно получиться так:
a b c d e f
a 1 1 0 -.5 -.5 0
b 1 1 0 -.5 -.5 0
c 0 0 1 0 0 1
d -.5 -.5 0 1 1 0
e -.5 -.5 0 1 1 0
f 0 0 1 0 0 1
Тоесть выражение вида: (a+b)^2 + (d+e)^2 + (c+f)^2 - a*d - a*e - b*d - b*e
Соответственно члены:
a=L/sqrt(3)
b=-b*cos(B)
c=b*sin(B)
d=-L/sqrt(3)
e=a*cos(A)
f=-a*sin(A)
Тогда забиваю в Wolfram Alpha:
(L/sqrt(3)-b*cos(B))^2 + (-L/sqrt(3)+a*cos(A))^2 + (b*sin(B)-a*sin(A))^2 + L*L/3 - a*L*cos(A)/sqrt(3) - b*L*cos(B)/sqrt(3) + a*b*cos(A)*cos(B)
и получаю:
a^2 + b^2 + L^2 -2*a*b*sin(A)*sin(B) +a*b*cos(A)*cos(B) -sqrt(3)*a*L*cos(A) -sqrt(3)*b*L*cos(B)
который условно можно разделить на 3 части:
1) a^2 + b^2 + L^2
2) -sqrt(3)*L*(a*cos(A)+b*cos(B))
3) a*b*(-2*sin(A)*sin(B) +cos(A)*cos(B)) = a*b*(1.5*cos(A+B)-0.5*cos(A-B))
в третьей части у меня выходит: 1.5*cos(A+B)-0.5*cos(A-B), у вас: cos(A+B)
где я туплю?
(Сообщение отредактировал thunder87l 19 июня 2012 15:05)
|
Всего сообщений: 29 | Присоединился: июнь 2012 | Отправлено: 19 июня 2012 13:54 | IP
|
|
thunder87l


Новичок
|
     
Было бы неплохо, если бы вы подтвердили либо опровергли моё решение, потому что этот член приводит к тому, что я толком не могу вынести cos(a). Если его там на самом деле нету и я ошибся - это здорово упростит мне жизнь ))
|
Всего сообщений: 29 | Присоединился: июнь 2012 | Отправлено: 20 июня 2012 3:09 | IP
|
|
MEHT


Долгожитель
|
     
Да, перепроверил свои выкладки и выявил ляп. Собрав коэффициенты при одинаковых векторах
%20%5Cvec{%5Ctau}_1%20+%20%5Cleft%20(a%5Csin%5Calpha%20%5Cright%20)%5Cvec{n}%20%5Cright%20)%20-%20%5Cleft%20(%5Cfrac{L}{%5Csqrt{3}}%5Ccdot%20%5Cvec{%5Ctau}_2%20-%5Cleft%20(b%5Ccos%5Cbeta%20%5Cright%20)%20%5Cvec{%5Ctau}_2%20+%20%5Cleft%20(b%5Csin%5Cbeta%20%5Cright%20)%5Cvec{n}%20%5Cright%20)%20=%5C%5C%5C%5C%20=%20%5Cleft%20(%5Cfrac{L}{%5Csqrt{3}}%20-%20a%5Ccos%5Calpha%20%5Cright%20)%20%5Cvec{%5Ctau}_1%20-%20%5Cleft%20(%5Cfrac{L}{%5Csqrt{3}}%20-%20b%5Ccos%5Cbeta%20%5Cright%20)%20%5Cvec{%5Ctau}_2%20+%20%5Cleft%20(a%5Csin%5Calpha%20-%20b%5Csin%5Cbeta%20%5Cright%20)%20%5Cvec%20{n})
возведение в квадрат даёт
%20%5Cvec{%5Ctau}_1%20-%20%5Cleft%20(%5Cfrac{L}{%5Csqrt{3}}%20-%20b%5Ccos%5Cbeta%20%5Cright%20)%20%5Cvec{%5Ctau}_2%20+%20%5Cleft%20(a%5Csin%5Calpha%20-%20b%5Csin%5Cbeta%20%5Cright%20)%20%5Cvec{n}%20%5Cright%20)^2%20=%5C%5C%5C%5C%5C%5C%20=%20%5Cleft%20(%5Cfrac{L}{%5Csqrt{3}}%20-%20a%5Ccos%5Calpha%20%5Cright%20)^2%20+%20%5Cleft%20(%5Cfrac{L}{%5Csqrt{3}}%20-%20b%5Ccos%5Cbeta%20%5Cright%20)^2%20+%20%5Cleft%20(a%5Csin%5Calpha%20-%20b%5Csin%5Cbeta%20%5Cright%20)^2%20+%20%5Cleft%20(%5Cfrac{L}{%5Csqrt{3}}%20-%20a%5Ccos%5Calpha%20%5Cright%20)%20%5Cleft%20(%5Cfrac{L}{%5Csqrt{3}}%20-%20b%5Ccos%5Cbeta%20%5Cright%20)%20=%20%5C%5C%5C%5C%20=%20L^2+a^2+b^2%20-%20L%5Csqrt{3}%5Cleft%20(%20a%5Ccos%5Calpha%20+%20b%5Ccos%5Cbeta%20%5Cright%20)%20+%20ab%5Cleft%20(%20%5Ccos%5Calpha%5Ccos%5Cbeta%20-%202%5Csin%5Calpha%20%5Csin%5Cbeta%20%5Cright%20))
и последнюю скобку уже не свернуть в косинус суммы как было записано у меня (потерял двойку у произведения синусов). Спасибо что перепроверили. Исправляю полученную систему.
Возможно, что теперь появятся подвижки в решении. Сразу оговорюсь, что возня с тригонометрией ничего не дала. Единственный выход - решать в лоб, т.е. "выразить из одного - подставить в другое".
Дальнейшие процедуры таковы - сначала переписать систему в безразмерном виде, поделив каждое уравнение на L². И от косинусов перейти к новым неизвестным x, y, z через соотношения
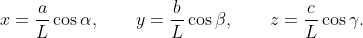
(Фактически это будут проекции векторов AD, BE, CF на плоскость нижнего треугольника делённые на L. Найдя их мы легко найдём и косинусы, а значит и углы.)
Система предстанет в виде
%20-%20x%20y%20+%202%5Csqrt{a^2-x^2}%5C,%5Csqrt{b^2-y^2}%20=%201%20-l^2+a^2+b^2,%20%5C%5C%20%5Csqrt{3}%20%5C,(y+z)%20-%20y%20z%20+%202%5Csqrt{b^2-y^2}%5C,%5Csqrt{c^2-z^2}%20=%201%20-l^2+b^2+c^2,%20%5C%5C%20%5Csqrt{3}%20%5C,(z+x)%20-%20z%20x%20+%202%5Csqrt{c^2-z^2}%5C,%5Csqrt{a^2-x^2}%20=%201%20-l^2+c^2+a^2.%20%5C%5C%20%5Cend{cases})
Тут под a, b, c уже следует понимать безразмерные a/L, b/L, c/L соответственно (я не стал обозначать их другими буквами, думаю и так будет понятно что к чему). Величину справа тоже удобно обозначить одной какой-нибудь буквой, дабы не таскать каждый раз единицу и три квадрата.
Радикалы в каждом уравнении можно вынести в правую часть, всё остальное - в левую, возвести обе части уравнения в квадрат, в результате получим систему трёх уравнений второго порядка, каждое из которых связывает по две неизвестных.
1-е и 3-е уравнения можно решать как квадратные относительно y и z, находим их через x (там будет двойственность значений как и при решении любого квадратного уравнения - для однозначности надо будет верно выбрать знак при корне из дискриминанта) и подставляем во 2-е - будет уравнение для икса, решив которое мы по сути решим и всю систему (аналогичные уравнения будут и для y и z).
Схема решения как будто ясна.. попробуйте воспользоваться. Я чуть позже тоже попытаюсь получить сиё уравнение для икса.
(Сообщение отредактировал MEHT 20 июня 2012 8:37)
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 20 июня 2012 4:42 | IP
|
|
MEHT


Долгожитель
|
     
Есть ещё соблазнительный вариант переписать синусы и косинусы исходной системы через комплексную экспоненту, сами комплексные экспоненты принять за неизвестные x, y, z. В результате тоже получается система уравнений второго порядка.
С учётом исправленной ошибки, возня с такой системой может и принесёт какие-то плоды..
(Сообщение отредактировал MEHT 20 июня 2012 5:56)
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 20 июня 2012 4:52 | IP
|
|
thunder87l


Новичок
|
     
Вы писали: для однозначности надо будет верно выбрать знак при корне из дискриминанта. Для меня эти вычисления уже потеряли всякий физический смысл )) поэтому я не совсем представляю чем руководствоваться при выборе корня. Брать из обоих уравнений первый?
Но я сделал как вы сказали - разделил на L^2, подставил x и y, заменил хвост на N, перетащил корни, возвёл в квадрат и получилось вот так:
x=a*cos(A)/L
y=b*cos(B)/L
a0=a/L
b0=b/L
N=1+(a^2+b^2-l^2)/L^2
возвожу в квадрат: (2*sqrt(a0^2-x^2)*sqrt(b0^2-y^2))^2 = (N -sqrt(3)*x -sqrt(3)*y +x*y)^2
4*(a0^2-x^2)*(b0^2-y^2) =
N^2 -sqrt(3)*N*x -sqrt(3)*N*y +N*x*y +
-sqrt(3)*N*x +3*x^2 +3*y*x -sqrt(3)*x^2*y +
-sqrt(3)*N*y +3*x*y +3*y^2 -sqrt(3)*x*y^2 +
N*x*y -sqrt(3)*x^2*y -sqrt(3)*x*y^2 +x^2*y^2
раскладываю по степеням:
-3 *x^2*y^2
-2*sqrt(3) *x^2*y
-2*sqrt(3) *x*y^2
(4*b0^2+3) *x^2
(4*a0^2+3) *y^2
(2*N+6) *x*y
-2*sqrt(3)*N *x
-2*sqrt(3)*N *y
N^2-4*a0^2*b0^2
затем Матлабом решаю относительно х:
x1= (3*y - 3^(1/2)*N + N*y + 2*(-(b0 + y)*(b0 - y)*(N^2 - 2*3^(1/2)*N*y - 4*a0^2*b0^2 + 3*a0^2*y^2 + 2*3^(1/2)*a0^2*y - 3*a0^2 + 3*y^2))^(1/2) - 3^(1/2)*y^2)/(- 4*b0^2 + 3*y^2 + 2*3^(1/2)*y - 3)
x2= -(3^(1/2)*N - 3*y - N*y + 2*(-(b0 + y)*(b0 - y)*(N^2 - 2*3^(1/2)*N*y - 4*a0^2*b0^2 + 3*a0^2*y^2 + 2*3^(1/2)*a0^2*y - 3*a0^2 + 3*y^2))^(1/2) + 3^(1/2)*y^2)/(- 4*b0^2 + 3*y^2 + 2*3^(1/2)*y - 3)
Что-то получил, но очень уж страшно ))
Подставлять в уравнения ещё не пробовал, боюсь - дело на весь день.
Три мысли сегодня приходили в голову:
1) Забавно что если l=0, всё это превращается в пирамиду, которую посчитать очень легко. На основании этого что-нибудь упростить можно? Может какие-то члены, в которых l не участвует внезапно обнуляются при рассмотрении пирамиды?
2) Вообще, наклон плоскости выражается двумя углами - наклон по осям X и Y. Может если перейти к этим двум углам - что-то упростится? Для простоты можно один из углов взять в плоскости вращения актуатора.
3) Если уравнения выглядят одинаково и позволяют циклические перестановки, не будет ли так, что в результате выразив из двух и подставив в третье получим просто ноль?
|
Всего сообщений: 29 | Присоединился: июнь 2012 | Отправлено: 21 июня 2012 3:57 | IP
|
|
luiza


Новичок
|
      
точка е-середина ребра дд1куба ABCDA1B1C1D1 найдите площадь сечения куба плоскостью B1CE если ребра куба равны 4
|
Всего сообщений: 2 | Присоединился: июнь 2012 | Отправлено: 21 июня 2012 13:44 | IP
|
|
luiza


Новичок
|
      
пожалуйста помогите решить
|
Всего сообщений: 2 | Присоединился: июнь 2012 | Отправлено: 21 июня 2012 13:45 | IP
|
|
thunder87l


Новичок
|
     
Ещё не решили?
Сечение задано треугольником ECB1. Сперва нужно достроить сечение. CB1 - диагональ квадрата, нужно построить паралельную прямую через E. Точка F - пересечение этой прямой с ребром A1D1, будет соответственно находиться в середине A1D1.
Сечение - равнобокая трапеция FB1CE.
B1C - диагональ квадрата, FE - половина от диагонали квадрата, EC и FB1 - гипотенуза треугольника с отношением катетов 0.5a:a.
B1C = 4*sqrt(2), EF = 2*sqrt(2), EC и FB1 = 2*sqrt(5)
Осталось найти высоту EE1 трапеции. EE1=3*sqrt(2) по т.Пифагора.
S=EF*EE1+0.5(B1C-EF)*EE1=12 + 6 = 18
Если я всё правильно понял, должно бы быть так.
|
Всего сообщений: 29 | Присоединился: июнь 2012 | Отправлено: 22 июня 2012 12:20 | IP
|
|
MEHT


Долгожитель
|
     
Выкладки громозки, ничего упростить не получилось, опишу как есть.
Три мысли сегодня приходили в голову:
1) Забавно что если l=0, всё это превращается в пирамиду, которую посчитать очень легко. На основании этого что-нибудь упростить можно? Может какие-то члены, в которых l не участвует внезапно обнуляются при рассмотрении пирамиды?
Это частный случай общей системы при заданном параметре, не более. Система слишком сложна тем, что в ней много параметров и они сложным образом увязаны друг с другом. Т.е. при различных a, b, c, l, система может как иметь решение, так и не иметь его, или же, чего я также не исключаю, будет давать более одного набора решений.
Простой пример: если при l=0 не выполнено условие a=b=c, то решений нет; или пусть даже оно и выполнено, но каждая безразмерная длина меньше 1/sqrt(3) - в этом случае тоже решений не будет (из таких длин просто-напросто будет не сложить пирамиды - короткие ребра).
2) Вообще, наклон плоскости выражается двумя углами - наклон по осям X и Y. Может если перейти к этим двум углам - что-то упростится? Для простоты можно один из углов взять в плоскости вращения актуатора.
Будет тоже самое. Мы же по сути записываем условия для векторов AD, BE, CF, а через косинусы или проекции они выражены наиболее просто, а следовательно проще будут и уравнения их связывающие.
Ориентацию плоскости задаёт её нормаль. Она характеризуется направляющими косинусами сумма квадратов которых единица.
Нормаль в свою очередь задаёт векторное произведение векторов DE и DF делённое на их длины, а выражены эти вектора через AD, BE, CF линейно (в прошлых постах я выписывал эти зависимости).
3) Если уравнения выглядят одинаково и позволяют циклические перестановки, не будет ли так, что в результате выразив из двух и подставив в третье получим просто ноль?
Нет, это исключено, ведь третье уравнение не есть следствие двух других. Каждое уравнение по сути выражает равенство длин векторов DE, EF, FD одной и той же величине l, а два равенства DE = l, EF = l, на основе которых написаны первые два уравнения, ещё не задают равностороннего треугольника.
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 24 июня 2012 17:14 | IP
|
|
MEHT


Долгожитель
|
     
Как ни крути, а проще станцевать от последней системы. Ужас в душу вселяют именно параметры - их много (аж 4 штуки) и они свободны в смысле независимых друг от друга неравенств:
a≥0, b≥0, c≥0, l≥0.
На него руки чешутся наложить ограничение: a≤b≤c (или a≥b≥c, непринципиально). Если одна из длин, скажем b при варьировании превысит a, мы просто переобозначим b ↔ a, и условие всегда будет выполнено. Такое ограничение способно внести хоть какой-то порядок в параметрах. Но и это в конечном счёте не упрощает самого процесса решения.
Далее я выпишу основные моменты. Само же непосредственное решение слишком сложно, не думаю что это вообще возможно в общем виде. Но зато при фиксированных a, b, c, l окончательное уравнение поддаётся численному решению, условия для отсеивания лишних корней будут выписаны - в конечном итоге всё вычисляемо.
Выражаем из первого уравнения y через x.
%20-%20x%20y%20+%202%5Csqrt{a^2-x^2}%5C,%5Csqrt{b^2-y^2}%20=%201%20-l^2+a^2+b^2%20%5Cequiv%20%5Cxi%20_c,%20%5C%5C%5C%5C%20%5Cleft%20(x-%5Csqrt{3}%20%5Cright%20)y%20+%20%5Cleft%20(%5Cxi%20_c%20-%20%5Csqrt{3}%20%5C,x%20%5Cright%20)=%202%5Csqrt{a^2-x^2}%5C,%5Csqrt{b^2-y^2},)
возводим обе части в квадрат
^2y^2%20%5C,+%20%5C,%202%5Cleft%20(x-%5Csqrt{3}%20%5Cright%20)%5Cleft%20(%5Cxi%20_c%20-%20%5Csqrt{3}%20%5C,x%20%5Cright%20)y%20%5C,+%5C,%5Cleft%20(%5Cxi%20_c%20-%20%5Csqrt{3}%20%5C,x%20%5Cright%20)^2=%204%5Cleft%20(a^2-x^2%20%5Cright%20)%5C,%5Cleft%20(b^2-y^2%20%5Cright%20),%5C%5C%5C%5C%20%5Cbegin{align*}%20%5Cleft%20[%5Cleft%20(x-%5Csqrt{3}%20%5Cright%20)^2%20+%204%5Cleft%20(a^2-x^2%20%5Cright%20)%20%5Cright%20]y^2%20%5C,%20&%20+%20%5C,%202%5Cleft%20(x-%5Csqrt{3}%20%5Cright%20)%5Cleft%20(%5Cxi%20_c%20-%20%5Csqrt{3}%20%5C,x%20%5Cright%20)y%20%5C,+%20%5C%5C%20&%20+%20%5C,%5Cleft%20(%5Cxi%20_c%20-%20%5Csqrt{3}%20%5C,x%20%5Cright%20)^2%20-%20%5C,4%20b^2%20%5Cleft%20(a^2-x^2%20%5Cright%20)=0,%20%5Cend{align*})
откуда
=%20%5Cfrac{-%5Cleft%20(x-%5Csqrt{3}%20%5Cright%20)%5Cleft%20(%5Cxi%20_c%20-%20%5Csqrt{3}%20%5C,x%20%5Cright%20)%5Cpm%20%5Csqrt{%5Cleft%20(x-%5Csqrt{3}%20%5Cright%20)^2%5Cleft%20(%5Cxi%20_c%20-%20%5Csqrt{3}%20%5C,x%20%5Cright%20)^2%20-%20%5Cleft%20[%5Cleft%20(x-%5Csqrt{3}%20%5Cright%20)^2%20+%204%5Cleft%20(a^2-x^2%20%5Cright%20)%20%5Cright%20]%5Ccdot%20%5Cleft%20[%20%5Cleft%20(%5Cxi%20_c%20-%20%5Csqrt{3}%20%5C,x%20%5Cright%20)^2%20-%20%5C,4%20b^2%20%5Cleft%20(a^2-x^2%20%5Cright%20)%20%5Cright%20]}}{%5Cleft%20(x-%5Csqrt{3}%20%5Cright%20)^2%20+%204%5Cleft%20(a^2-x^2%20%5Cright%20)}.)
(Случай равенства нулю знаменателя рассмотрим потом отдельно.)
Тут могут быть лишние корни, возможное появление которых следует пресекать неравенством
y%20+%20%5Cleft%20(%5Cxi%20_c%20-%20%5Csqrt{3}%20%5C,x%20%5Cright%20)%5Cgeqslant%200.)
Это условие следует непосредственно из исходного уравнения (вторая формула) - положительность правой части очевидна как произведение положительных радикалов, соответственно положительной должна быть и левая часть. Геометрически его можно трактовать как условие, отбрасывающее решения отвечающие за пересечения плоскостей верхнего и нижнего треугольников (т.е. когда вершины D и E верхнего треугольника оказались в разных полупространствах относительно плоскости основания ABC, а условие равносторонности тр. DEF тем не менее выполнено).
Также сюда следует добавить естественные ограничения на x и y (опять таки следует из исходного уравнения):
%20%5Cleqslant%20b.)
Само существование (вещественных) y - есть условие неотрицательности дискриминанта; пишем:
^2%5Cleft%20(%5Cxi%20_c%20-%20%5Csqrt{3}%20%5C,x%20%5Cright%20)^2%20-%20%5Cleft%20[%5Cleft%20(x-%5Csqrt{3}%20%5Cright%20)^2%20+%204%5Cleft%20(a^2-x^2%20%5Cright%20)%20%5Cright%20]%5Ccdot%20%5Cleft%20[%20%5Cleft%20(%5Cxi%20_c%20-%20%5Csqrt{3}%20%5C,x%20%5Cright%20)^2%20-%20%5C,4%20b^2%20%5Cleft%20(a^2-x^2%20%5Cright%20)%20%5Cright%20]%20%5Cgeqslant%200.)
Всё тоже самое записывается для уравнения связывающего x и z.
---
Теперь рассмотрим случай когда знаменатель в зависимости y1,2=y(x) обращается в нуль. Это возможно только в случае
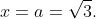
Исходное уравнение вырождается до вида
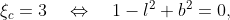
что отвечает параметрам b=0, l=1 и как следствие y=0 (случай l>1 рассматривается отдельно по аналогии).
Для z и c соответственно: z=c=0.
Уравнение связывающее y и z также удовлетворяется этим "особым" решением.
Наглядно этот результат представляет собой картину, когда верхний треугльник, по размерам равный нижнему, полностью лёг в плоскость нижнего так, что сторона EF совпала с BC. (Такой случай исключителен, Ваше устройство его не реализует. Но уравнениям "всё равно" - они охватывают все возможные комбинации положения треугольников, поэтому и нужны ограничения в виде неравенств.
(Сообщение отредактировал MEHT 27 июня 2012 14:45)
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 24 июня 2012 17:27 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 1.25 Стереометрия
1.25 Стереометрия

 Форум
Форум

 Математика
Математика

 1.25 Стереометрия
1.25 Стереометрия