attention 
Долгожитель
|
     
Цитата: kicez написал 13 дек. 2009 20:55
Помогите, пожалуйста, вычислить площадь фигуры ограниченной линией
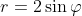
Данное уравнение в полярных координатах задает окружность с единичным радиусом.
^2\,d\varphi = 2\int\limits_0^\pi \sin^2\varphi\,d\varphi = \hfill \\ = \int\limits_0^\pi (1 - \cos 2\varphi)\,d\varphi = \left. {\left(\varphi - \frac{1}{2}\sin 2\varphi \right)} \right|_0^\pi = \pi . \hfill \\ \end{gathered} )
Смотрите график (зеленым отмечена область интегрирования)
(Сообщение отредактировал attention 20 фев. 2010 14:11)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 14 дек. 2009 6:30 | IP
|
|
Jmagath
Новичок
|
Здравствуйте, помогите пожалуста решить задачу.
Найти объем тела, полученного при вращении вокруг оси OY фигуры, ограниченной линиями:
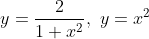
Заранее спасибо.
(Сообщение отредактировал attention 20 фев. 2010 14:13)
|
Всего сообщений: 15 | Присоединился: январь 2008 | Отправлено: 18 дек. 2009 15:39 | IP
|
|
Dmitry28
Новичок
|
Помагите с парой задач
Найи массу пласины ограниченной линией L=x^2+y^2)^2=a^2(x^2-y^2) (x>0, y>0)
поверх. плотность=sqrt(a^2-x^2-y^2)
Вычислиь мом инерции полусферы z=sqrt(R^2-x^2-y^2) относительно плоскости YOZ, если плотность =y^2
и вопросик x^2+y^2+z^2-2z=0 как это выглядит в пространсве
Спасибо
Подскажите хоть немного..
|
Всего сообщений: 16 | Присоединился: февраль 2009 | Отправлено: 20 фев. 2010 1:28 | IP
|
|
Svetochka87
Новичок
|
Помогите решить
|
Всего сообщений: 20 | Присоединился: март 2010 | Отправлено: 2 марта 2010 16:25 | IP
|
|
Svetochka87
Новичок
|
Помгите пожалуйста решить :
Вычислить объем тела, полученного при вращении вокуг оси ох фигуры, оганиченной линиями
y^2=4-x y=-x/2+2
|
Всего сообщений: 20 | Присоединился: март 2010 | Отправлено: 2 марта 2010 16:27 | IP
|
|
Svetochka87
Новичок
|
Помогите пожалуйста дорешать
Вычислить длину дуги кривой, заданной уравнениями.
y=lnsinx-1 x ot pi\4 do pi/3
L=sqrt(1+(dy/dx)^2)=
=sqrt (1+cos^2x/sin^2x)=sqrt(1/sin^2x)
выводим из под корня получается: 1/sinx
L=интеграл от pi/4 нижняя ганица д pi/3 верхняя граница
интеграл dx/sinx= ln(2sin(x/2))-ln(2cos(x/2))
помогите пожалуйста у меня если подставлять такой ужас получается
|
Всего сообщений: 20 | Присоединился: март 2010 | Отправлено: 2 марта 2010 16:29 | IP
|
|
Flashmob
Новичок
|
Здравствуйте!!!
Помогите решить,пожалуйста!
Вычислить момент инерции окружности радиуса a относительно ее диаметра.
|
Всего сообщений: 1 | Присоединился: март 2010 | Отправлено: 6 марта 2010 6:58 | IP
|
|
Svetochka87
Новичок
|
Спасибо большое за помощь в решении не могли бы вы мне еще немножко помочь, примеры легкие только я совсем не помню как они решаются.
1.Найти критические точки первого рода и интервалы монотонности функции y= (x^2+6)/(x^2+1)
2.Исследовать на экстремум функцию y=2(x+1)^2/(x-2)
3.Найти интервалы выпуклости и вогнутости, точки перегиба графика функции y=(2x^2+2+4x)/(2-x)
4.Найти ассимптоты графика функции y=(2x^2-9)/sqrt(x^2-1)
|
Всего сообщений: 20 | Присоединился: март 2010 | Отправлено: 9 марта 2010 8:27 | IP
|
|
RKI
Долгожитель
|
Цитата: Svetochka87 написал 9 марта 2010 8:27
3.Найти интервалы выпуклости и вогнутости, точки перегиба графика функции y=(2x^2+2+4x)/(2-x)
 = \frac{2x^{2} + 4x + 2}{2-x} )
 = (-\infty;2) \cup (2;+\infty) )
 = \frac{-2x^{2} + 8x + 10}{(2-x)^{2} } )
 = \frac{36}{(2-x)^{3} } )
 = 0 )
^{3} } = 0 )
Данное уравнение не имеет решений. Следовательно, исходная функция не имеет точек перегиба.
y'' + _
_____________________________________
2
Функция вогнута на промежутке . ) Функция выпукла на промежутке . )
(Сообщение отредактировал RKI 10 марта 2010 13:23)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 9 марта 2010 19:52 | IP
|
|
Svetochka87
Новичок
|
Большое вам прибольшое спасибо!!!
|
Всего сообщений: 20 | Присоединился: март 2010 | Отправлено: 9 марта 2010 20:50 | IP
|
|
Форум
2.1.14 Приложения интегрального исчисления
