thunder87l


Новичок
|
     
Добрый день,
У меня одна задачка, с которой я себе уже весь мозг вынес. Делаю штуку, которая с помощью трёх линейных актуаторов позиционирует платформу в пространстве. Задачка выглядит так:
1) есть основание - правильный треугольник ABC, ребро длинной в m
2) есть платформа - правильный треугольник DEF, ребро длинной в n
3) есть три линейных актуатора (штука такая - выталкивает металлический поршень на столько, на сколько нужно) - это рёбра AD, BE, CF соответственно.
4) длинна актуатора состоит из суммы двух параметров: L - длинны корпуса актуатора, и N - длинны выдвинутого поршня. L - величина постоянная, а N - переменная в пределах от 0 до 0.5L.
5) соединение с основанием ABC сделано таким образом, что каждый актуатор может вращаться вокруг точки соединения с ABC, в одной плоскости. Эта плоскость задаётся перпендикуляром к плоскости ABC и высотой треугольника ABC опущеной из соответствующей точки соединения.
[Если не понятно - актуатор установлен на ось в точке А. Ось находится в плоскости основания и паралельна BC. И так - каждый из трёх.]
6) соединение с плоскостью DEF - свободное, тоесть - треугольник DEF может находиться в любом положении относительно точки соединения.
Что ещё могу сказать? В состоянии когда все актуаторы одинаково выдвинуты, ABC и DEF паралельны и образуют усечённую пирамиду.
Собственно необходимо - определить положение плоскости DEF (углы наклона относительно ABC) исходя из m, n, a, b, c, где a, b и c - соответствуют длинне каждого из актуаторов.
|
Всего сообщений: 29 | Присоединился: июнь 2012 | Отправлено: 16 июня 2012 4:37 | IP
|
|
MEHT


Долгожитель
|
     
Цитата: thunder87l написал 16 июня 2012 4:37
Ось находится в плоскости основания и паралельна BC.
Наверное "перпендикулярна" ? Иначе картинку не представить.
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 16 июня 2012 11:19 | IP
|
|
thunder87l


Новичок
|
     
Да нет. Ось таки паралельна BC, а вот предмет посаженый на ось (актуатор) - вражается перпендикулярно BC.
Кстати да, я забыл, что можно задать плоскость нормалью и точкой. Так наверное было бы проще объяснить. Плоскость в которой вращается актуатор перпендикулярна BC и содержит A.
|
Всего сообщений: 29 | Присоединился: июнь 2012 | Отправлено: 16 июня 2012 12:52 | IP
|
|
thunder87l


Новичок
|
     
Пришла в голову дикая мысль. Сперва AD=BE=CF и плоскости паралельны. Затем увеличим длинну одного ребра, например - AD. Мне кажется, что это не должно повлиять на положение двух других рёбер, потому что плоскости в которых они вращаются не паралельны одна другой, а сверху они связаны ребром треугольника EF. таким образом они по идее не должны двигаться. А значит EF не изменит положения, когда AD вытянется. Если это правильно, то единственное изменение - DEF повернётся на сколько-то градусов вокруг EF.
А вот если AD и BE и CF сначала не равны - тут мне уже нехватает фантазии.
|
Всего сообщений: 29 | Присоединился: июнь 2012 | Отправлено: 17 июня 2012 1:17 | IP
|
|
thunder87l


Новичок
|
     
Ок, предыдущее предположение проиграл в голове раз 15-20 - вроде работает. Если два других актуатора равны, а третий меняет длинну, происходит вращение DEF вокруг ребра которое держат два других актуатора.
Только это - очевидно частный случай. От обратного: Если бы это был общий случай, то выглядело бы следующим образом: актуатор AD уменьшился, плоскость DEF повернулась вокруг EF на n градусов. Затем актуатор BE уменьшился - плоскость DEF опять повернулась, только на этот раз - вокруг ребра DF. Только DF уже находится под углом к плоскости ABC. Актуатор который вращается в одной плоскости не может повернуть DEF вокруг DF, потому что они не перпендикулярны.
Но то что я раньше сказал - работает, значит - нужно найти более общий случай. Мне кажется что ротация происходит не вокруг DF, а вокруг центра ребра DF, в плоскости работы актуатора, но доказать или опровергнуть это у меня пока не получается.
Опять-же - терзают смутные сомнения, что этот центр подвижен, пока плоскость совершает поворот. Может у меня маразм, но мне так почему-то кажется.
|
Всего сообщений: 29 | Присоединился: июнь 2012 | Отправлено: 17 июня 2012 2:43 | IP
|
|
MEHT


Долгожитель
|
     
Вы имели ввиду ось вращения рёбер, способных менять свою длину. Простите, не сразу понял о какой оси речь 
То есть схематично картинка следующая:

Сверху и снизу равносторонние треугольники, длина боковых рёбер варьируются.
На рисунке я обозначил три угла, которые ребра образуют с плоскостью нижнего треугольника - насколько я понял Вы именно их ищите, ведь фактически они и задают ориентацию верхней плоскости. Так? Поправьте если где-то неточно.
Мне удалось получить систему трёх уравнений для этих углов. Система сама по себе не громозкая, чего не скажешь о решении. Алгоритм решения в принципе ясен, но муторен; я его не проводил. Думал найти "красивое" решение, но пока безрезультатно. И похоже на то, что громозкости так или иначе не миновать.. 
Позже я распишу сам вывод.
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 17 июня 2012 3:34 | IP
|
|
thunder87l


Новичок
|
     
Да, да - это именно то что имелось ввиду. Спасибо большое.
P.S. В чём вы нарисовали такую классную картинку?
(Сообщение отредактировал thunder87l 17 июня 2012 14:16)
|
Всего сообщений: 29 | Присоединился: июнь 2012 | Отправлено: 17 июня 2012 14:11 | IP
|
|
MEHT


Долгожитель
|
     
В "ГИС Панорама" (это специфический софт, используемый для создания цифровых топографических карт), но в принципе для рисовки подошёл бы и любой другой редактор векторной графики. Просто я одно время работал как раз в этой сфере и на этом софте, вот и остались навыки..
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 18 июня 2012 0:11 | IP
|
|
MEHT


Долгожитель
|
     
Итак. Для начала исходные данные. Заданы сторона нижнего L и верхнего l треугольников (можно также считать что L>l) и длины боковых рёбер a, b, c. Неизвестными считаем углы, составляющие этими рёбрами с плоскостью нижнего треугольника, обозначим их через α, β, γ.
Из центра нижнего треугольника (на рисунке букв не проставлено, но обзовём этот центр буквой O) проведём три единичных вектора к вершинам А, В, С и обозначим их 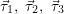 , а также ещё один единичный вектор , а также ещё один единичный вектор 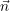 перпендикулярно плоскости треугольника. На рисунке эти векторы я показал красным. перпендикулярно плоскости треугольника. На рисунке эти векторы я показал красным.
Каждый вектор в плоскости составляет с любым из соседних векторов плоскости угол в 2п/3 и каждый из них перпендикулярен 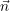 . Поэтому . Поэтому
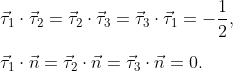
Вектора AD, BE, CF находятся каждый в своей плоскости:
АD в плоскости векторов 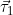 и и 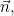
BE в плоскости векторов 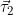 и и 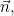
CF в плоскости векторов 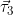 и и 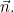
(строго говоря, помимо этих векторов плоскости задают ещё и общая для всех их точка O)
Каждый из них распишется по единичным векторам:
%20%5Cvec{%5Ctau}_1%20+%20%5Cleft%20(a%5Csin%5Calpha%20%5Cright%20)%5Cvec{n}%5C,%20,%5C%5C%5C%5C%20%5Cvec{BE}%20=%20-%5Cleft%20(b%5Ccos%5Cbeta%20%5Cright%20)%20%5Cvec{%5Ctau}_2%20+%20%5Cleft%20(b%5Csin%5Cbeta%20%5Cright%20)%5Cvec{n}%5C,%20,%5C%5C%5C%5C%20%5Cvec{CF}%20=%20-%5Cleft%20(c%5Ccos%5Cgamma%20%5Cright%20)%20%5Cvec{%5Ctau}_3%20+%20%5Cleft%20(c%5Csin%5Cgamma%20%5Cright%20)%5Cvec{n}%5C,)
куда уже входят наши искомые углы и длины ребер.
Известно, что верхний треугольник равносторонний со стороной l, а это означает, что
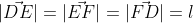
или же
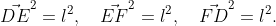
Вектора слева этих уравнений можно переписать через наши единичные вектора:
%20-%20(%5Cvec{OA}+%5Cvec{AD})%20=%20%5C%5C%5C%5C%20=%5Cleft%20(%5Cfrac{L}{%5Csqrt{3}}%5Ccdot%20%5Cvec{%5Ctau}_2%20-%5Cleft%20(b%5Ccos%5Cbeta%20%5Cright%20)%20%5Cvec{%5Ctau}_2%20+%20%5Cleft%20(b%5Csin%5Cbeta%20%5Cright%20)%5Cvec{n}%20%5Cright%20)%20-%20%5Cleft%20(%5Cfrac{L}{%5Csqrt{3}}%5Ccdot%20%5Cvec{%5Ctau}_1%20-%5Cleft%20(a%5Ccos%5Calpha%20%5Cright%20)%20%5Cvec{%5Ctau}_1%20+%20%5Cleft%20(a%5Csin%5Calpha%20%5Cright%20)%5Cvec{n}%20%5Cright%20),%5C%5C%5C%5C%5C%5C%20%5Cvec{EF}=%5Cleft%20(%5Cfrac{L}{%5Csqrt{3}}%5Ccdot%20%5Cvec{%5Ctau}_3%20-%5Cleft%20(c%5Ccos%5Cgamma%20%5Cright%20)%20%5Cvec{%5Ctau}_3%20+%20%5Cleft%20(c%5Csin%5Cgamma%20%5Cright%20)%5Cvec{n}%20%5Cright%20)%20-%20%5Cleft%20(%5Cfrac{L}{%5Csqrt{3}}%5Ccdot%20%5Cvec{%5Ctau}_2%20-%5Cleft%20(b%5Ccos%5Cbeta%20%5Cright%20)%20%5Cvec{%5Ctau}_2%20+%20%5Cleft%20(b%5Csin%5Cbeta%20%5Cright%20)%5Cvec{n}%20%5Cright%20),%5C%5C%5C%5C%5C%5C%20%5Cvec{FD}=%5Cleft%20(%5Cfrac{L}{%5Csqrt{3}}%5Ccdot%20%5Cvec{%5Ctau}_1%20-%5Cleft%20(a%5Ccos%5Calpha%20%5Cright%20)%20%5Cvec{%5Ctau}_1%20+%20%5Cleft%20(a%5Csin%5Calpha%20%5Cright%20)%5Cvec{n}%20%5Cright%20)%20-%20%5Cleft%20(%5Cfrac{L}{%5Csqrt{3}}%5Ccdot%20%5Cvec{%5Ctau}_3%20-%5Cleft%20(c%5Ccos%5Cgamma%20%5Cright%20)%20%5Cvec{%5Ctau}_3%20+%20%5Cleft%20(c%5Csin%5Cgamma%20%5Cright%20)%5Cvec{n}%20%5Cright%20).)
Эти вектора сходны по форме написания. Циклические перестановки
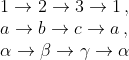
переводят их один в другой.
Поэтому имеет смысл рассмотреть только одно уравнение системы, скажем
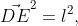
остальные выпишутся по аналогии в соответствие с цикличностью.
Сами выкладки по возведению 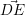 в квадрат довольно длинны, поэтому не выписываю (Вы можете самостоятельно их провести - заодно и сверитесь, а то вдруг я где-нибудь опечатался); окончательно уравнение сводится к такому: в квадрат довольно длинны, поэтому не выписываю (Вы можете самостоятельно их провести - заодно и сверитесь, а то вдруг я где-нибудь опечатался); окончательно уравнение сводится к такому:
%20-%20ab%20%5Cleft%20(%5Ccos%5Calpha%20%5Ccos%5Cbeta%20-%202%5Csin%5Calpha%20%5Csin%5Cbeta%5Cright%20)%20=%20L^2-l^2+a^2+b^2,)
а вся система, следовательно, будет иметь вид:
%20-%20ab%20%5Cleft%20(%5Ccos%5Calpha%20%5Ccos%5Cbeta%20-%202%5Csin%5Calpha%20%5Csin%5Cbeta%5Cright%20)%20=%20L^2-l^2+a^2+b^2,%20%5C%5C%20L%5Csqrt{3}%20%5C,(b%5Ccos%5Cbeta%20+c%5Ccos%5Cgamma%20)%20-%20bc%20%5Cleft%20(%5Ccos%5Cbeta%20%5Ccos%5Cgamma%20-%202%5Csin%5Cbeta%20%5Csin%5Cgamma%20%5Cright%20)%20=%20L^2-l^2+b^2+c^2,%20%5C%5C%20L%5Csqrt{3}%20%5C,(c%5Ccos%5Cgamma%20+a%5Ccos%5Calpha%20)%20-%20ca%20%5Cleft%20(%5Ccos%5Cgamma%20%5Ccos%5Calpha%20-%202%5Csin%5Cgamma%20%5Csin%5Calpha%20%5Cright%20)%20=%20L^2-l^2+c^2+a^2.%20%5Cend{cases})
(Сообщение отредактировал MEHT 27 июня 2012 14:38)
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 18 июня 2012 0:43 | IP
|
|
MEHT


Долгожитель
|
     
С решением, как я уже говорил, всё сложнее. Каждое уравнение системы связывает между собой два искомых угла, т.е. имеет вид
f(cos α , cos β ) = 0.
Цель - получить систему, каждое уравнение которой включало бы в себя только одну неизвестную, т.е. уравнение вида
f(cos α ) = 0.
Алгоритм прямого решения таков:
из одного уравнения выражаем cos β как функцию от cos α,
из другого уравнения, соответственно cos γ как функцию от cos α ,
подставляем их в оставшееся и имеем уравнение вида f(cos α ) = 0.
Аналогично для других углов.
Вручную такое решать конечно же никому не захочется. На машине ещё можно попробовать..
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 18 июня 2012 0:54 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 1.25 Стереометрия
1.25 Стереометрия

 Форум
Форум

 Математика
Математика

 1.25 Стереометрия
1.25 Стереометрия