Lav
Новичок
|
     
Большое спасибо за решение. А что именно находится этим интегралом? Масса?
|
Всего сообщений: 18 | Присоединился: июнь 2008 | Отправлено: 27 дек. 2008 13:41 | IP
|
|
ProstoVasya
Долгожитель
|
Да, конечно. У Вас в условии задачи написано, что линейная плотность в каждой её точке обратно прапорциональна ординате этой точки, т.е. 1/y, ds -элемент длины.
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 27 дек. 2008 20:12 | IP
|
|
Lav
Новичок
|
Ещё раз большое спасибо. Теперь более менее ясно.
|
Всего сообщений: 18 | Присоединился: июнь 2008 | Отправлено: 27 дек. 2008 21:56 | IP
|
|
daimos
Новичок
|
 
Помогите пожалуйста решить криволинейный интеграл первого рода
 ,если l-дуга кривой  от точек
 до точки 
2. Криволинейный интеграл 2 рода
(интегрирование провести в положительном направлени)
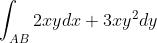 ,если AB-отрезок прямой что соиденяет точки A(1;1), B(2;4)
По первому
int(x^2 dl) = int (x^2*sqrt(1+(y')^2) dx)
но дальше? а второй вообще незнаю как
Зарание большое спасибо вам!
Я извеняюсь просто думал можно постить там где упоминается интеграл. Сорри  .
(Сообщение отредактировал attention 7 дек. 2009 1:49)
|
Всего сообщений: 19 | Присоединился: декабрь 2008 | Отправлено: 1 дек. 2009 10:37 | IP
|
|
Marushka1989
Новичок
|
Вычислить криволинейный интеграл
где кривая L задана параметрически x=cos t; y=sin t, 0<=t<=Pi/2
Заранее спасибо
|
Всего сообщений: 4 | Присоединился: декабрь 2009 | Отправлено: 21 дек. 2009 22:31 | IP
|
|
Solomon
Новичок
|
помогите пожалуйста вычислить кривол.интеграл 2 рода по С, (х^2dy-xydx), где С: х^2+у^2=4, непосредственно по формулам, и проверить по формуле Грина
|
Всего сообщений: 11 | Присоединился: октябрь 2009 | Отправлено: 22 дек. 2009 22:07 | IP
|
|
Solomon
Новичок
|
пожалуйста, помогите...горю((( срочно нужно решение
|
Всего сообщений: 11 | Присоединился: октябрь 2009 | Отправлено: 27 дек. 2009 17:15 | IP
|
|
marsvetlanka
Новичок
|
1. Вычислить с помощью двойного интеграла в полярных координатах
площадь фигуры, ограниченной кривой, заданной уравнением в декартовой системе
(а>0) y^6=f^6(x^2+y^2)(3y^2-x^2)
2. Вычислить криволинейный инт int y/x dx +x dy вдоль дуги L кривой y=ln x
от точки А(1;0) до точки В (е;1). Сделать чертеж
3.Вычислить с помощью тройного интеграла объем тела, ограниченного
указанными поверхностями. Сделать чертежи данного тела и его проекции на
плоскость хОу. z=0, z=4* корень.кв.у, х+у=4
Заранее благодарна
|
Всего сообщений: 32 | Присоединился: январь 2009 | Отправлено: 29 дек. 2009 11:38 | IP
|
|
studentka2010
Новичок
|
Здравтсвуйте! Выручите пожалйста, ну ооочень необходимо.
Убедительная просьба помочь разобраться со следующим заданием:
вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривыми, заданными уравнениями в декартовых координатах
x^2+y^2-2y=0
x^2+y^2+2x=0
Решала следующим образом.
Приводила к виду:
x^2 + (y-1)^2 = 1
(x+1)^2 + y^2 = 1
Переходила к полярным координатам:
x=r*Cos(phi)
y=r*Sin(phi)
Получила:
r1 = 2Sin(phi)
r2 = -2Cos(phi)
phi попробовала взять по чертежу (я брала от pi/2 до pi)
Подставляла все это дело в формулу и получила 0.
Выручайте, подскажите чего делать... Я понимаю что тут по другому как-то надо, но не понимаю как...
|
Всего сообщений: 3 | Присоединился: январь 2010 | Отправлено: 8 янв. 2010 23:38 | IP
|
|
studentka2010
Новичок
|
Хоть бы кто-нибудь чего-нибудь ответили... вообще стоит нет ответа ждать? Или может чего не правильно написано?
|
Всего сообщений: 3 | Присоединился: январь 2010 | Отправлено: 9 янв. 2010 2:12 | IP
|
|
Форум
2.1.10 Криволинейные интегралы
